A solid sphere rolls without slipping on a rough horizontal floor, moving with a speed v. It makes an elastic collision with a smooth vertical wall. After impact
(a)it will move with a speed v initial
(b)its motion will be rolling with slipping initially and its rotational motion will stop momentarily at some instant.
(c)its motion will be rolling without slipping only after some time
(d)all of the above.
To solve the problem of a solid sphere rolling without slipping on a rough horizontal floor and making an elastic collision with a smooth vertical wall, we can break down the situation step by step.
Step 1: Understand the Initial Conditions
- The solid sphere is rolling without slipping with a speed v.
- The angular velocity ω of the sphere is related to its translational speed by the equation:
v=rω
where r is the radius of the sphere.
Step 2: Analyze the Collision
- The sphere makes a perfectly elastic collision with a smooth vertical wall.
- In a perfectly elastic collision, the speed of the center of mass remains the same, but the direction of the velocity changes.
Step 3: Determine the Velocity After Collision
- Before the collision, the velocity of the sphere is v (to the right).
- After the collision, the translational velocity of the sphere will change direction but maintain the same magnitude. Therefore, the new velocity v′ after the collision is:
v′=−v
Step 4: Analyze Angular Velocity
- The angular velocity ω of the sphere before the collision is:
ω=vr
- After the collision, the force from the wall acts at the center of mass, and since the torque about the center of mass is zero, the angular velocity remains unchanged immediately after the collision:
ω′=ω
Step 5: Determine the Point of Contact Velocity
- The velocity of the point of contact P with respect to the ground after the collision can be expressed as:
vP=v′+ω′⋅r
Substituting the values:
vP=−v+(vr)⋅r=−v+v=0
- This shows that the point of contact does not slip immediately after the collision.
Step 6: Analyze the Motion After Collision
- Since the sphere is rolling without slipping immediately after the collision, it will continue to roll until friction acts on it.
- The friction will oppose the motion and will cause an angular deceleration.
Step 7: Conclusion
- The sphere will initially continue with speed v but in the opposite direction.
- The rotational motion will momentarily stop due to the friction acting on it.
- Eventually, the sphere will return to rolling without slipping after some time.
Final Answer
Based on the analysis, the correct statements regarding the motion of the sphere after the collision are:
1. It will move with a speed v (but in the opposite direction).
2. Its motion will be rolling with slipping initially, and its rotational motion will stop momentarily.
3. It will be rolling without slipping only after some time.
Thus, the correct answer is option D, as all statements are correct.
- The solid sphere is rolling without slipping with a speed v.
- The angular velocity ω of the sphere is related to its translational speed by the equation:
v=rω
where r is the radius of the sphere.
- The sphere makes a perfectly elastic collision with a smooth vertical wall.
- In a perfectly elastic collision, the speed of the center of mass remains the same, but the direction of the velocity changes.
- Before the collision, the velocity of the sphere is v (to the right).
- After the collision, the translational velocity of the sphere will change direction but maintain the same magnitude. Therefore, the new velocity v′ after the collision is:
v′=−v
- The angular velocity ω of the sphere before the collision is:
ω=vr
- After the collision, the force from the wall acts at the center of mass, and since the torque about the center of mass is zero, the angular velocity remains unchanged immediately after the collision:
ω′=ω
- The velocity of the point of contact P with respect to the ground after the collision can be expressed as:
vP=v′+ω′⋅r
Substituting the values:
vP=−v+(vr)⋅r=−v+v=0
- This shows that the point of contact does not slip immediately after the collision.
- Since the sphere is rolling without slipping immediately after the collision, it will continue to roll until friction acts on it.
- The friction will oppose the motion and will cause an angular deceleration.
- The sphere will initially continue with speed v but in the opposite direction.
- The rotational motion will momentarily stop due to the friction acting on it.
- Eventually, the sphere will return to rolling without slipping after some time.
Based on the analysis, the correct statements regarding the motion of the sphere after the collision are:
1. It will move with a speed v (but in the opposite direction).
2. Its motion will be rolling with slipping initially, and its rotational motion will stop momentarily.
3. It will be rolling without slipping only after some time.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective
32 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Assertion And Reason
11 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A solid sphere rolling on a rough horizontl surface with a lilner speed v collides elastically with a fixed, smooth, vertical wall. Find the speed of the sphere after it has started pure rolling in the backward direction.
View SolutionA 1 Kg solid sphere rolls without slipping on a rough horizontal suface as shown in figure. Select incorrect alternative

View SolutionWhen a body is rolling without slipping on a rough horizontal surface, the work done by friction is :
View SolutionA solid sphere rolling on a rough horizontal surface. Acceleration of contact point is zero.
A solid sphere can roll on the smooth surface.
View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. If collides elastically with an identical another sphere at rest. There is no friction between the two spheres . Radius of each sphere is R and mass is m.
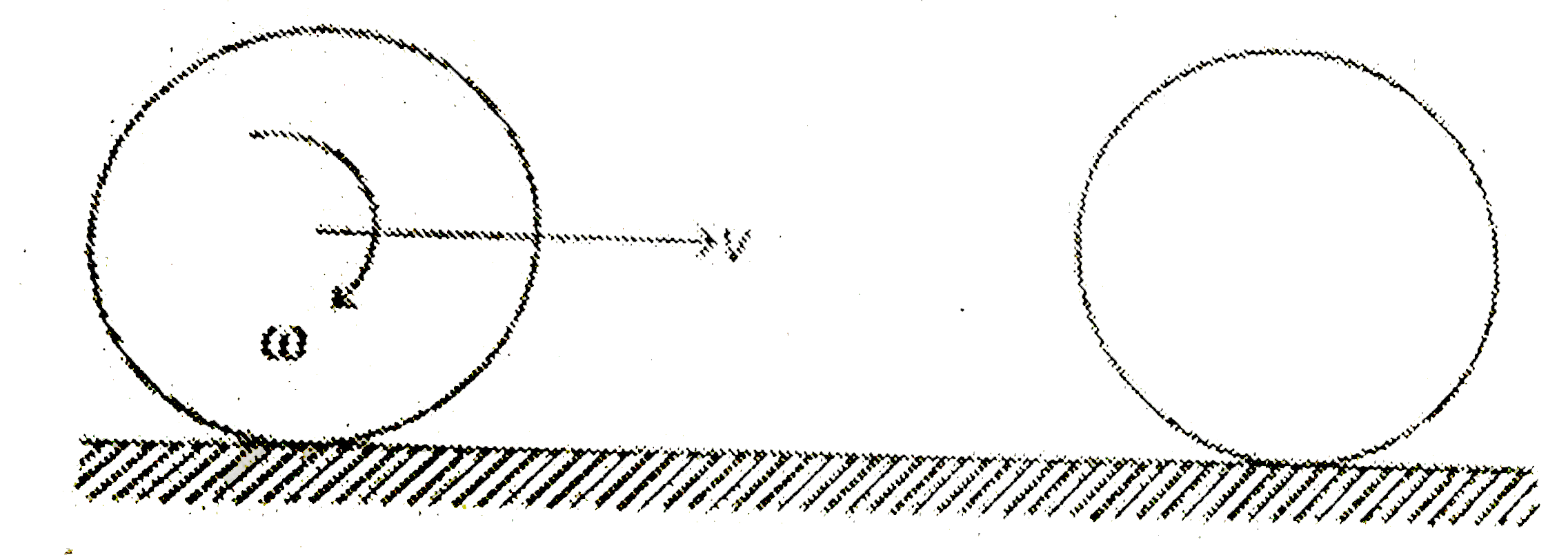
Linear velocity of first sphere after it again starts rolling without slipping is
View SolutionA ball of radius R=20cm has mass m=0.75kg and moment of inertia (about its diameter ) I=0.0125kgm2. The ball rolls without sliding over a rough horizontal floor wilth velocity v0=10ms−1 towards a smooth vertical wall if coefficient of resutitution between the wall and the ball is e=0.7, calculate velocity v of the ball long after the collision. (g=10ms−2)
View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. If collides elastically with an identical another sphere at rest. There is no friction between the two spheres . Radius of each sphere is R and mass is m.
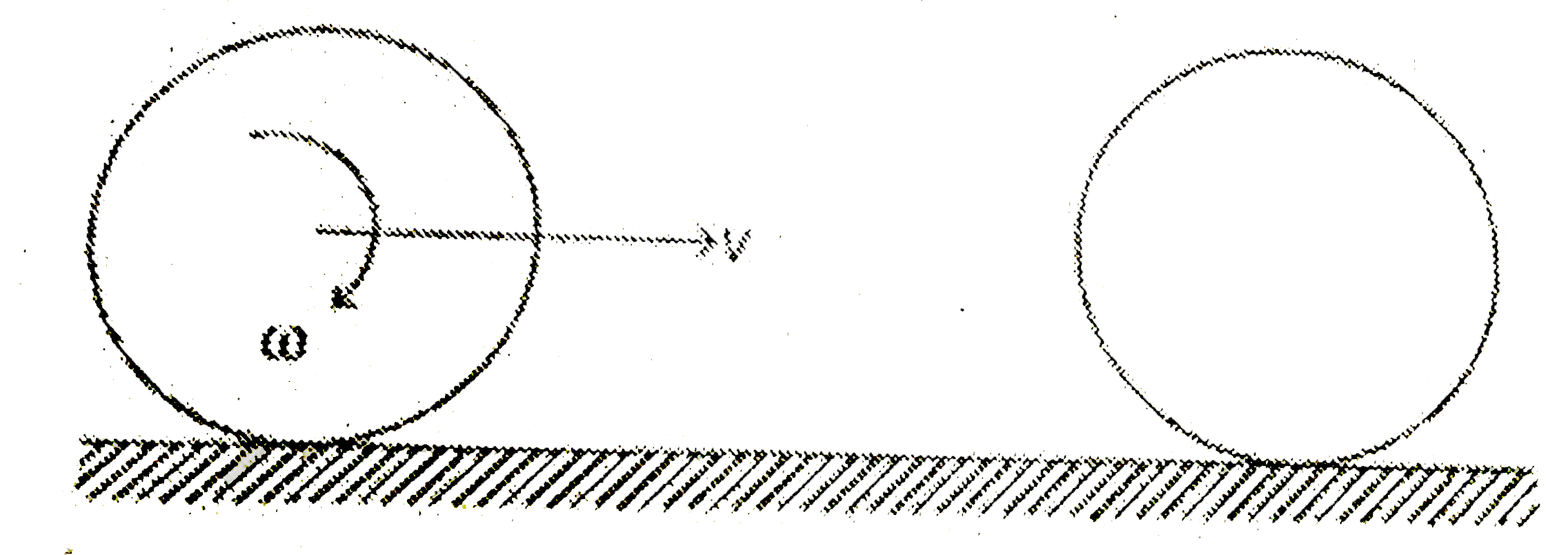
What is the net angular impulse imparted to second sphere by the external forces?
View SolutionA ball rolls without sliding over a rough horizontal floor with velocity v0=7m/s towards a smooth vertical wall. If coefficient of restitution between the wall and the ball is e=0.7. Calculate velocity v of the ball after the collision.
View Solution
A solid sphere is rolling purely on a rough horizontal surface (coefficient of kinetic friction =μ) with speed of centre =u. It collides inelastically with a smooth vertical wall at a certain moment, the coefficient of restituting being 12. The sphere will begin pure rolling after a time.
View SolutionTwo identical balls are rolling without slipping on a horizontal plane as shwon in figure. They undergo a perfect elastic collision. Just after collision, the velocity of image of the bottom point of A with respect to the plane mirros is x V, then x=

View Solution
