Two identical discs are positioned on a vertical axis as shown in the figure. The bottom disc is rotating at angular velocity ω0 and has rotational kinetic energy K0.The top disc is initially at rest. It then falls and sticks to the bottom disc. The change in the rotational kinetic energy of the system is

K0/2
−K0/2
−K0/4
K0/4
K=L22I or K∝1I As I has doubled, so K will become half.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective
32 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Assertion And Reason
11 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
View Solution
A solid disc is rolling without slipping on a horizontal ground as shown in figure. Its total kinetic energy is 100 J. what is its translational and rotational kinetic energy?
View SolutionA disc is rolling on a surface without slipping. What is the ratio of its translational to rotational kinetic energies ?
View SolutionA disc is rolling without slipping. The ratio of its rotational kinetic energy and translational kinetic energy would be -
View SolutionTwo uniform circular rough disc of moment of inertia I1 and I12 are rotating with angular velocity ω1 and ω12 respectively in same direction. Now one disc is placed the other disc co-axially. The change in kinetic energy of the system is :
View SolutionA disc is rotaing with an angular velocity ω0. A constant retarding torque is applied on it to stop the disc. The angular velocity becomes ω02 after n rotations. How many more rotations will it make before coming to rest ?
View SolutionA quarter disc of radius R and mass m is rotating about the axis OO' (perpendicular to the plane of the disc) as shown. Rotational kinetic energy of the quarter disc is
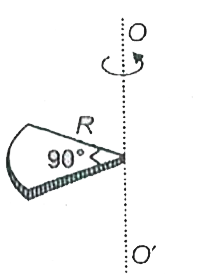
View SolutionA circular disc rolls down an inclined plane . The ratio of rotational kinetic energy to total kinetic energy is
View SolutionA disc of mass 4.8 kg and radius 1 m is rolling on a horizontal surface without sliding with angular velocity of 600 rotations/min. What is the total kinetic energy of the disc ?
View SolutionA disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity ω. The force acting on the disc is
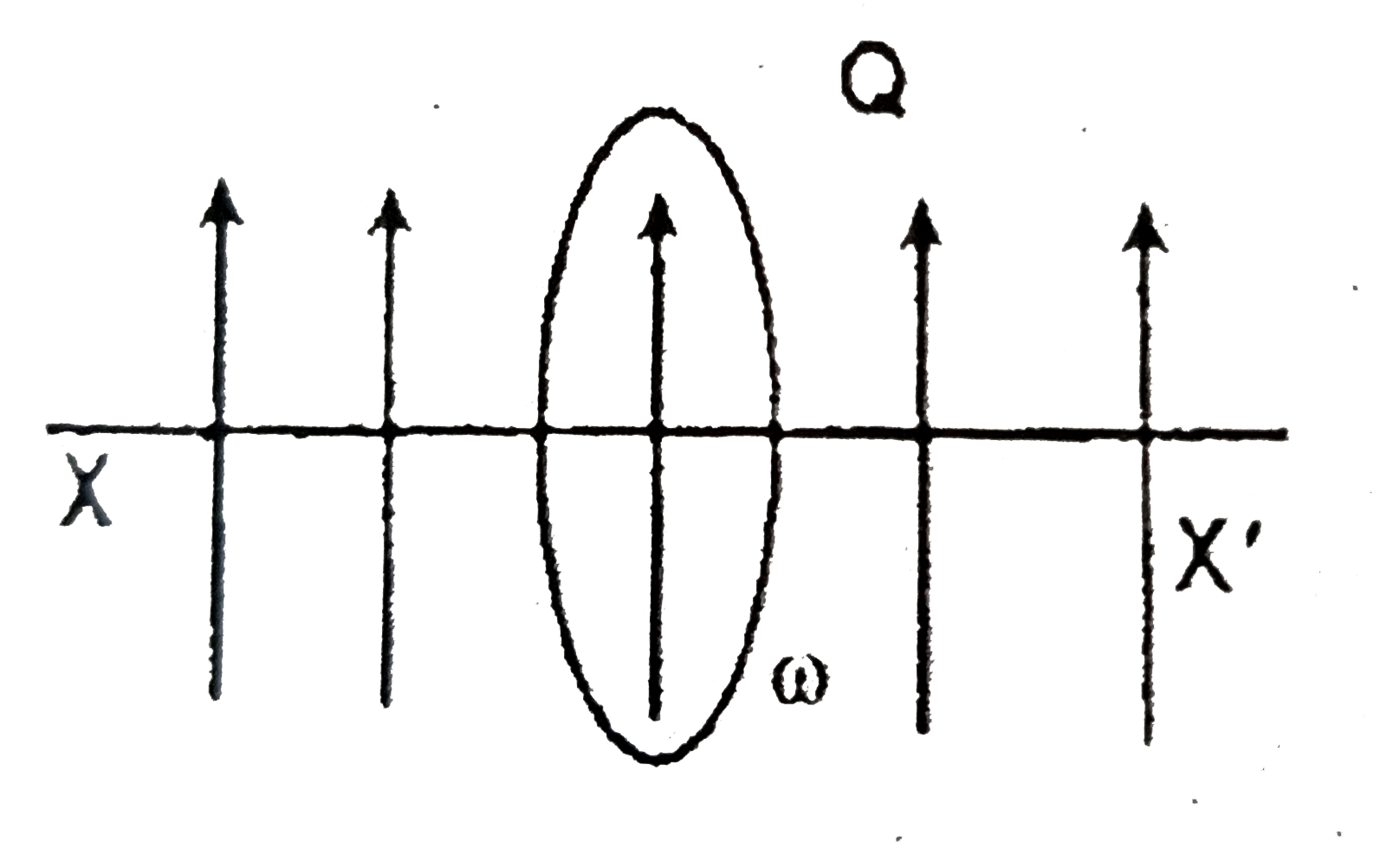
View Solution
