For the same total mass, which of the following will have the largest moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the body
(a)a disc of radius R
(b)a ring of radius R
(c)a square lamina of side 2 R
(d)four rods forming a square of side 2R
The correct Answer is:D
To determine which object has the largest moment of inertia about an axis passing through its center of mass and perpendicular to the plane of the body, we will calculate the moment of inertia for each given shape: a disc, a ring, a square lamina, and four rods forming a square.
Step 1: Moment of Inertia of a Disc
The moment of inertia I of a disc about an axis through its center and perpendicular to its plane is given by the formula:
Idisc=12mr2
where m is the mass and r is the radius of the disc.
Step 2: Moment of Inertia of a Ring
The moment of inertia I of a ring about an axis through its center and perpendicular to its plane is given by:
Iring=mr2
where m is the mass and r is the radius of the ring.
Step 3: Moment of Inertia of a Square Lamina
For a square lamina with side length 2r, the moment of inertia about an axis through its center and perpendicular to its plane is:
Isquare=16m(2r)2=23mr2
Step 4: Moment of Inertia of Four Rods Forming a Square
Each rod has a length of 2r and a mass of m4. The moment of inertia of one rod about its center is given by:
Irod=112mrodL2=112(m4)(2r)2=mr212
Using the parallel axis theorem to find the moment of inertia about the center of the square, we have:
Itotal=Irod+mrodd2
where d is the distance from the center of the square to the center of the rod (which is r):
Itotal=mr212+(m4)r2=mr212+mr24=mr212+3mr212=4mr212=mr23
Since there are four rods, the total moment of inertia for the square formed by four rods is:
Isquare rods=4×mr23=4mr23
Step 5: Comparison of Moments of Inertia
Now we have the moments of inertia for each shape:
1. Disc: Idisc=12mr2
2. Ring: Iring=mr2
3. Square Lamina: Isquare=23mr2
4. Four Rods: Isquare rods=43mr2
Step 6: Conclusion
Comparing these values:
- Idisc=12mr2
- Isquare=23mr2
- Isquare rods=43mr2
- Iring=mr2
The largest moment of inertia is for the ring, followed by the four rods forming a square.
Thus, the object with the largest moment of inertia about an axis passing through the center of mass and perpendicular to the plane of the body is the ring.
The moment of inertia I of a disc about an axis through its center and perpendicular to its plane is given by the formula:
Idisc=12mr2
where m is the mass and r is the radius of the disc.
The moment of inertia I of a ring about an axis through its center and perpendicular to its plane is given by:
Iring=mr2
where m is the mass and r is the radius of the ring.
For a square lamina with side length 2r, the moment of inertia about an axis through its center and perpendicular to its plane is:
Isquare=16m(2r)2=23mr2
Each rod has a length of 2r and a mass of m4. The moment of inertia of one rod about its center is given by:
Irod=112mrodL2=112(m4)(2r)2=mr212
Using the parallel axis theorem to find the moment of inertia about the center of the square, we have:
Itotal=Irod+mrodd2
where d is the distance from the center of the square to the center of the rod (which is r):
Itotal=mr212+(m4)r2=mr212+mr24=mr212+3mr212=4mr212=mr23
Since there are four rods, the total moment of inertia for the square formed by four rods is:
Isquare rods=4×mr23=4mr23
Now we have the moments of inertia for each shape:
1. Disc: Idisc=12mr2
2. Ring: Iring=mr2
3. Square Lamina: Isquare=23mr2
4. Four Rods: Isquare rods=43mr2
Comparing these values:
- Idisc=12mr2
- Isquare=23mr2
- Isquare rods=43mr2
- Iring=mr2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective
32 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Assertion And Reason
11 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A uniform thin bar of mass 6m and length 12L is bend to make a regular hexagon. Its moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the hexagon is :
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
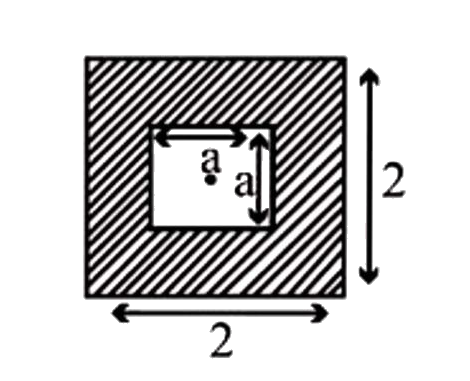
View SolutionA square of a side a is cut from a square of side 2a as shown in the figure. Mass of this square with a hole is M. Then its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane will be
View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :

View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passing through its centre of mass and perpendicular to the plane of the particle.
View SolutionTwo discs have same mass and thickness. Their materials are of densities d1andd2. The ratio of their moments of inertia about an axis passing through the centre and perpendicular to the plane is
View Solutionfind moment of inertia about an axis yy which passes through the centre of mass of the two particle system as shown

View SolutionTwo rings of same radius and mass are placed such that their centres are at a common point and their planes are perpendicular to each other. The moment of inertia of the system about an axis passing through the centre and perpendicular to the plane of one of the rings is (mass the ring =m, radius=r)
View SolutionOne circular ring and one circular disc, both are having the same mass and radius. The ratio of their moments of inertia about the axes passing through their centres and perpendicular to their planes, will be
View Solution
