
A solid sphere is rolling purely on a rough horizontal surface (coefficient of kinetic friction ) with speed of centre . It collides inelastically with a smooth vertical wall at a certain moment, the coefficient of restituting being . The sphere will begin pure rolling after a time.

Pure rolling will start when
or
solving we get,
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective
32 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A solid sphere rolling on a rough horizontal surface. Acceleration of contact point is zero.
A solid sphere can roll on the smooth surface.
View SolutionA solid sphere rolling on a rough horizontl surface with a lilner speed v collides elastically with a fixed, smooth, vertical wall. Find the speed of the sphere after it has started pure rolling in the backward direction.
View SolutionA solid sphere rolls without slipping on a rough horizontal floor, moving with a speed v. It makes an elastic collision with a smooth vertical wall. After impact
View SolutionA solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to

View SolutionA sphere of mass m is rolling without sliding along positive x-axis on a rough horizontal surface of coefficient of friction μ. It elastically collides with a wall and then returns. The correct statement of frictional force (f) acting on the sphere is
View SolutionA solid sphere of mass m= 500gm is rolling without slipping on a horizontal surface. Find kinetic energy of a sphere if velocity of centre of mass is 5 cm/sec
View SolutionA uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity V and angular velocity ω(V=ωr). The sphere collides with a sharp edge on the wall as shown in Fig. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the sphere just after the collision is equal to
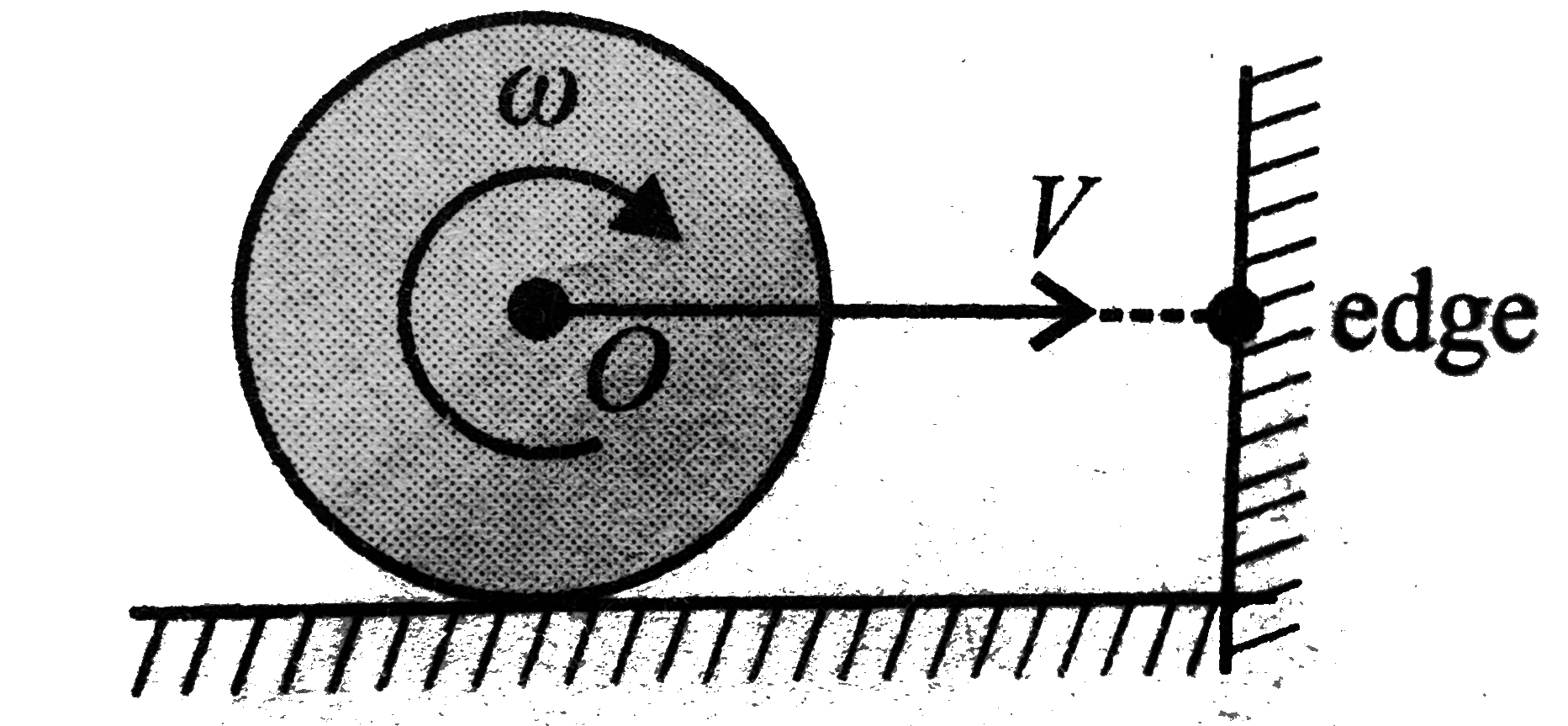
View SolutionA cylinder is rolling towards a cube of same mass on rough horizontal surface ( coefficient of friction = μ) with velocity v0 as shown in figure. Assume elastic collision and friction is negligible between cube and cylinder. Then after collision

View SolutionA smooth sphere of mass m is moving on a horizontal plane with a velocity (3ˆi+ˆj) . It collides with smooth a vertical wall which is parallel to the vector ˆj . If coefficient of restitution e=12 then impulse that acts on the sphere is
View SolutionA smooth sphere is moving on a horizontal surface with velocity vector 2ˆi+2ˆj immediately before it hits a vertical wall. The wall is parallel to ˆj and the coefficient of restitution of the sphere and the wall is e=12. Find the velocity of the sphere after it hits the wall?
View Solution
