
A stationary uniform rod in the upright position is allowed to fall on a smooth horizontal surface. The figure shows the instantaneous position of the rod. Identify the correct statement.
1) Normal reaction N is equal
to Mg
2) N does positive rotational work about the centre of mass
3) A couple of equal and opposite forces acts on the rod
4) All of the above
normal reaction N is equal to Mg
N does positive rotational work about the centre of mass
a couple of equal and opposite forces acts on the rod
all of the above.
Mg can't provide rotatainal motion. This is only N which actually provides the rotational motion.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective
32 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A uniform straight rod is placed in vertical position on a smooth horizontal surface and released. As the rod is in motion, the centre of mass moves
View Solution
One-fourth length of a uniform rod of mass m and length l is placed on a rough horizontal surface and it is held stationary in horizontal position by means of a light thread as shown in the figure. The thread is then burnt and the rod start rotating about the edge. Find the angle between the rod and the horizontal when it is about to slide on the edge. The coefficient of friction between the rod and surface is μ.
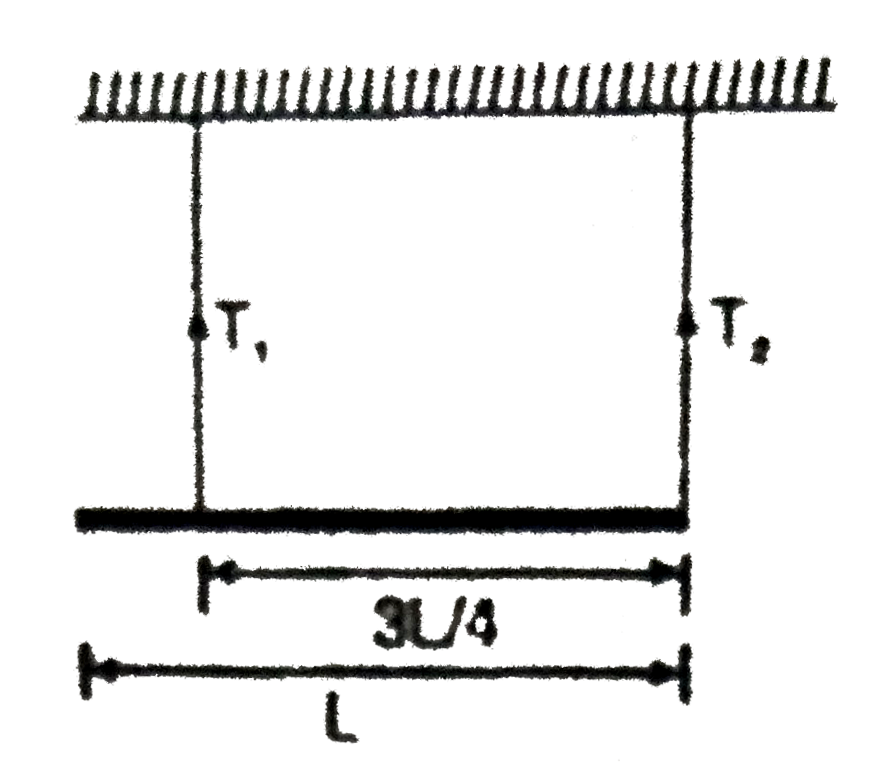
View SolutionA uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1T2 is:
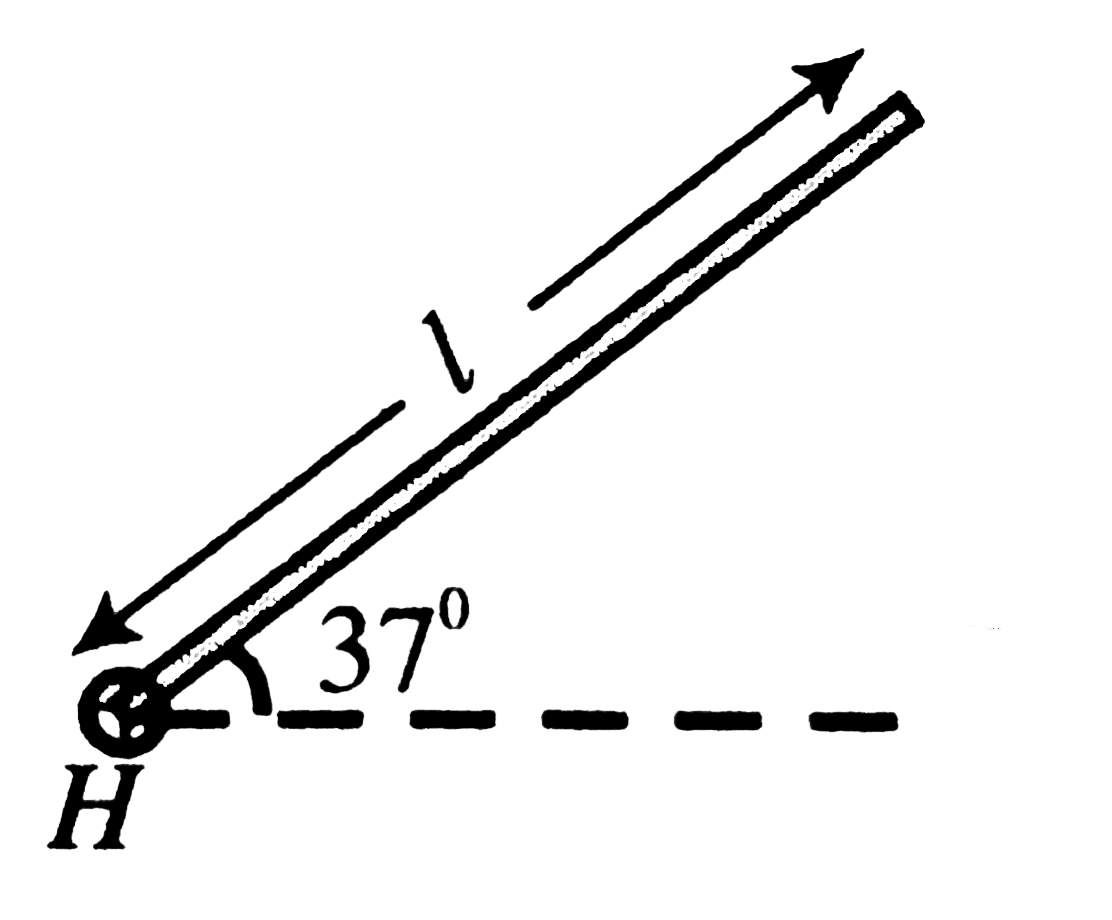
View SolutionA uniform rod of mass m and length l can rotate in vertical plane about a smooth horizontal axis hinged at point H. Find angular acceleration α of the rod just after it is released from initial position making an angle of 37∘ with horizontal from rest?
View SolutionA uniform thin rod of mass m and length L is standing vertically along the y-axis on a smooth horizontal surface, with its lower end at the origin (0,0). A slight disturbane at t = 0 causes the lower end t slip on the smooth surface along the positive x-axis, and the rod starts falling.
(i) What is the path followed by the centr of mass of the rod during its fall?
(ii) Find the equaiton to the trajectory of a point on the rod shape of the path of this point?
View SolutionA 5kg rod of square cross section 5cm on a side and 1m long is pulled along a smooth horizontal surface by a force applied at one end. The rod has a constant acceleration of 2ms−12. Determine the elongation in the rod. (Young's modulus of the material of the rod is 5×103N/m9).
View SolutionTwo blocks of masses 4kg and 2kg are placed side on a smooth horizontal surface as shown in the figure. A horizontal force of 20N is applied on 4kgblock. Find
(a) the acceleration of each block.
(b) the normal reaction between two blocks.

View SolutionTwo blocks of masses 4kg and 2kg are placed side on a smooth horizontal surface as shown in the figure. A horizontal force of 20N is applied on 4kgblock. Find
(a) the acceleration of each block.
(b) the normal reaction between two blocks.

View Solution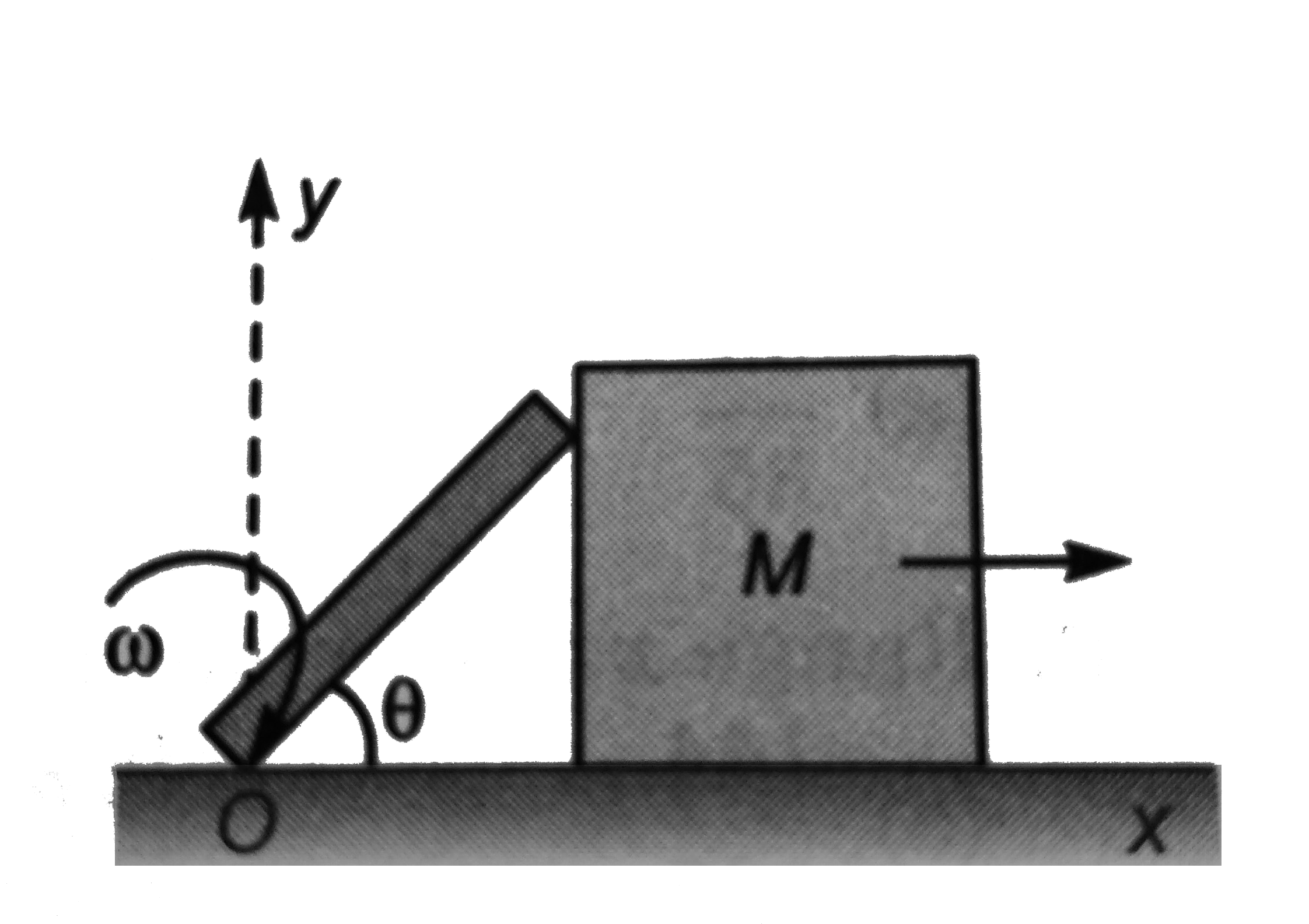
A uniform rod of mass m and length l is applied pivoted at point O. The rod is initially in vertical position and touching a block of mass M which is at rest on a horizontal surface. The rod is given a slight jerk and it starts rotating about point O this causes the block to move forward as shown The rod loses contact with the block at θ=30∘ all surfaces are smooth now answer the following questions.
Q. The acceleration of centre of mass of rod, when it loses contact with the block is
View SolutionA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml23, the initial angular acceleration of the rod will be

View Solution
