A solid ball of mass m and radius r spinning with angular velocity ω falls on a horizontal slab of mass M with rough upper surface (coefficient of friction μ) and smooth lower surface. Immediately after collision the normal component of velocity of the ball remains half of its value just before collision and it stops spinning. Find the velocity of the sphere in horizontal direction immediately after the impact (given: Rω=5).
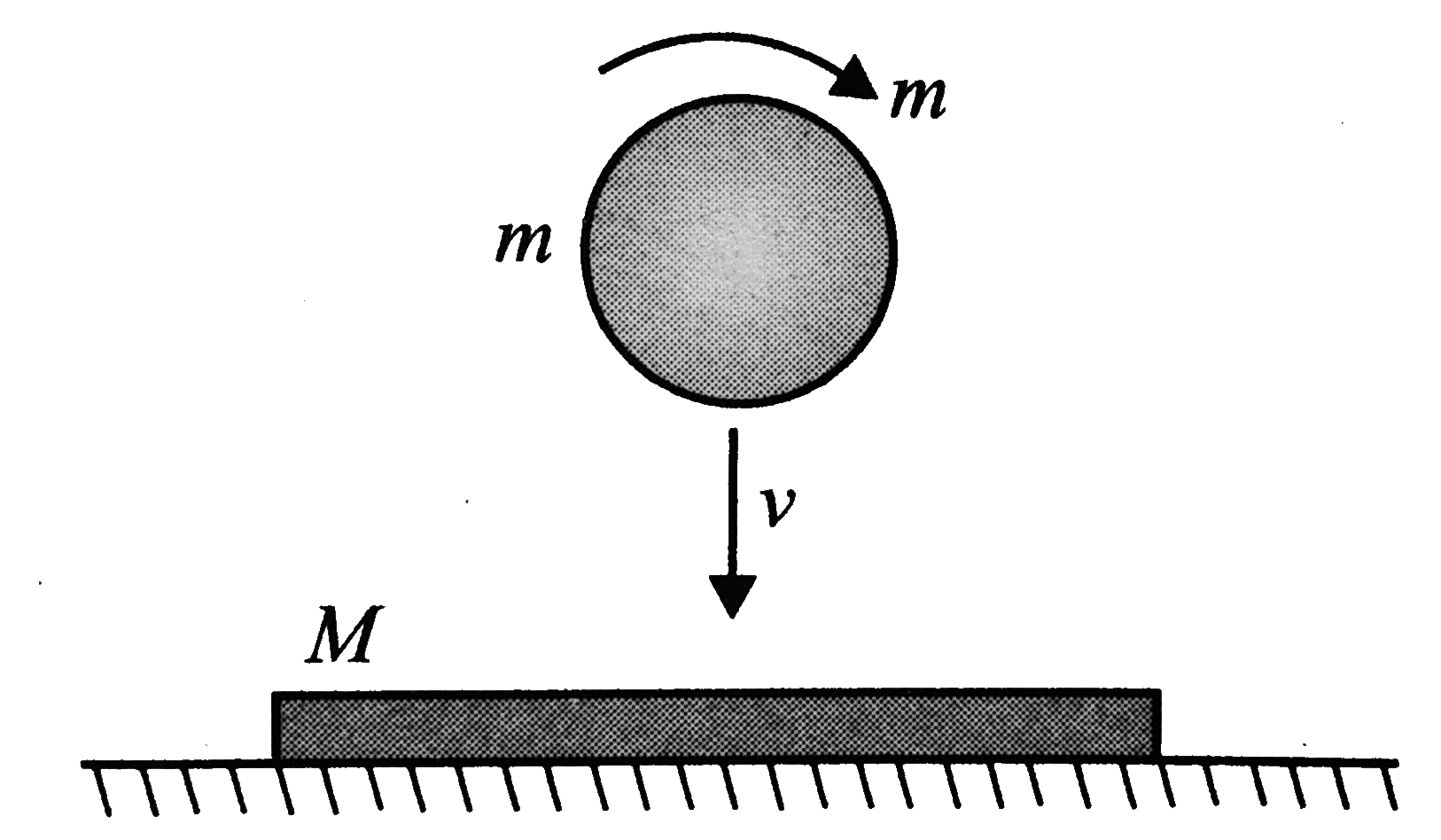
The correct Answer is:2
J=∫Ndt=mv2−(−mv)=32,mv………..i
μJR=∫μ(Ndt)R=(25mR2ω−0)=25mR2ω……..ii

From eqn i and ii we get
32mvrμ=25mR2ω……….iii
let V and V1 be the speeds of the plank and the sphere, respectively in the horizontal direction.
μJ=∫mjNdt=Mv=mV1........iv
Form eqn i and iv μ(32)mv=MV
V=32μmvM=32415mRωM=25Rω
and V1=25Rω=2m/s
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Fill In The Blanks
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
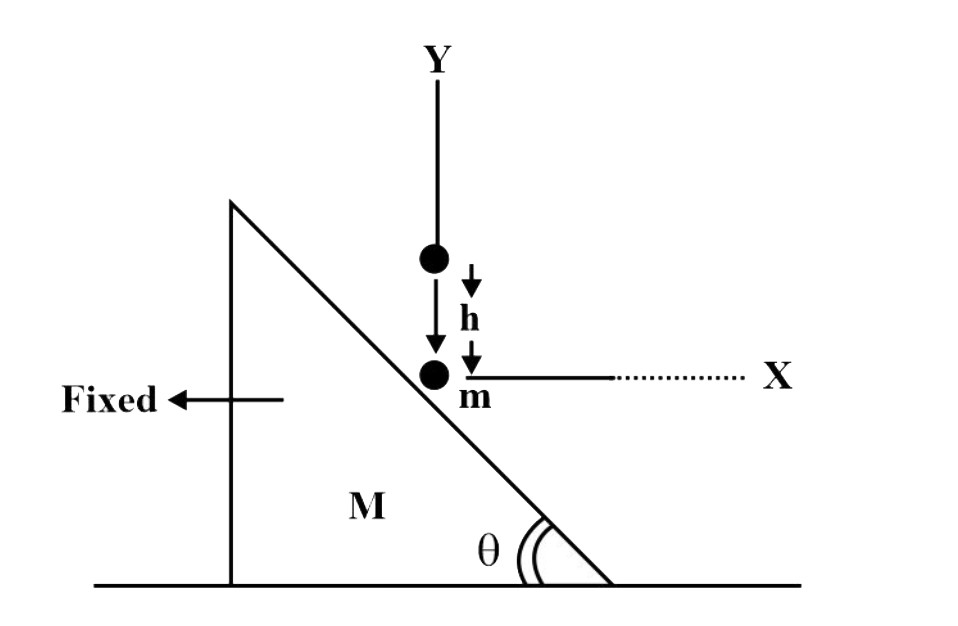
View SolutionA ball of mass m is dropped onto a smooth fixed wedge of inclination θ The collision is perfectly elastic . If after the collision, the x component of the velocity of the block is √2gh , then θ is
View SolutionA ball of mass m moving with velocity u collides head-on which the second ball of mass m at rest. If the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
View SolutionA ball of mass m moving with velocity v collides head-on which the second ball of mass m at rest. I the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
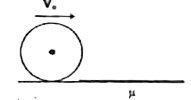
View SolutionA ring of mass m sliding on a smooth surface with velocity v0 enters rough surface with coefficient of kinetic friction μk, then
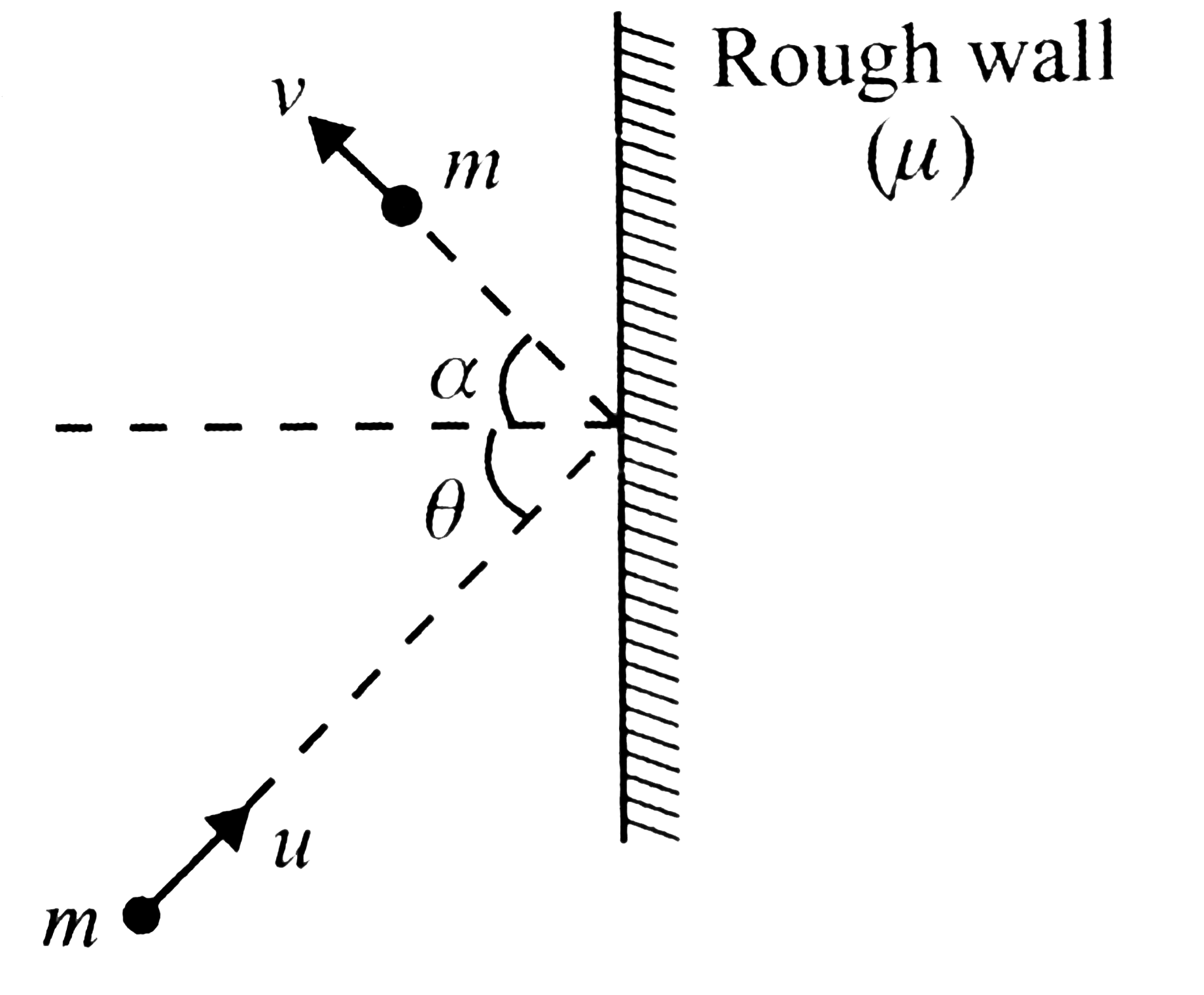
View SolutionA small ball of mass m collides with as rough wal having coeficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves wilth angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.
View SolutionA cylinder is rolling towards a cube of same mass on rough horizontal surface ( coefficient of friction = μ) with velocity v0 as shown in figure. Assume elastic collision and friction is negligible between cube and cylinder. Then after collision

View SolutionA ball of mass m collides with a stationary wedge of mass M, perpendicular to its inclined face, inclined at an angle as shown in the figure. If the coefficient of restitution between the wedge and ball is e, calculate the ratio of modulus of velocity of the ball immediately after and before collision. Also calculate the velocity of wedge just after collision.

View SolutionA ball is moving with velocity 2m/s towards a heavy wall moving towards the ball with speed 1m/s as shown in figure. Assuming collision to be elastic, find the velocity of ball immediately after the collision.

View SolutionA ball is moving with velocity 2m/s towards a heavy wall moving towards the ball with speed 1m/s as shown in figure. Assuming collision to be elastic, find the velocity of ball immediately after the collision.

View Solution
