A thin uniform rod of length l is initially at rest with respect to an inertial frame of reference. The rod is tapped at one end perpendicular to its length. How far the centre of mass translates while the rod completes one revolution about its centre of mass. Neglect gravitational effect.
To solve the problem step by step, we will analyze the motion of the rod after it is tapped and how far the center of mass translates while the rod completes one full revolution about its center of mass.
Step 1: Understanding the System
We have a thin uniform rod of length l that is initially at rest. When tapped at one end, it begins to rotate about its center of mass. The center of mass of the rod is located at its midpoint, which is at a distance of l2 from either end.
Hint: Identify the center of mass of the rod and understand the effect of the impulse applied at one end.
Step 2: Impulse and Change in Momentum
When the rod is tapped, an impulse J is applied at one end. The change in momentum ΔP can be expressed as:
J=ΔP=mvc−0=mvc
where vc is the velocity of the center of mass after the impulse.
Hint: Recall that impulse is equal to the change in momentum and relate it to the velocity of the center of mass.
Step 3: Angular Impulse and Change in Angular Momentum
The angular impulse about the center of mass can be expressed as:
J⋅l2=ΔL
where ΔL is the change in angular momentum. The moment of inertia I of the rod about its center of mass is given by:
I=ml212
Thus, we can write:
J⋅l2=I⋅ω
Substituting for I:
J⋅l2=ml212⋅ω
Hint: Use the relationship between linear impulse and angular momentum to connect linear and angular quantities.
Step 4: Relating Linear Velocity to Angular Velocity
From the impulse equation, we can express ω:
J=mvcandJ=ml212⋅6vcl
This leads to:
ω=6vcl
Hint: Simplify the equations to find the relationship between linear velocity and angular velocity.
Step 5: Time to Complete One Revolution
The time t taken to complete one full revolution (where ωt=2π) can be expressed as:
t=2πω=2πl6vc=πl3vc
Hint: Use the relationship between angular displacement and time to find the period of rotation.
Step 6: Distance Translated by the Center of Mass
The distance xc traveled by the center of mass during this time can be calculated as:
xc=vc⋅t=vc⋅πl3vc=πl3
Hint: Use the formula for distance traveled, which is speed multiplied by time.
Final Answer
The center of mass translates a distance of:
πl3 while the rod completes one revolution about its center of mass.
We have a thin uniform rod of length l that is initially at rest. When tapped at one end, it begins to rotate about its center of mass. The center of mass of the rod is located at its midpoint, which is at a distance of l2 from either end.
When the rod is tapped, an impulse J is applied at one end. The change in momentum ΔP can be expressed as:
J=ΔP=mvc−0=mvc
where vc is the velocity of the center of mass after the impulse.
The angular impulse about the center of mass can be expressed as:
J⋅l2=ΔL
where ΔL is the change in angular momentum. The moment of inertia I of the rod about its center of mass is given by:
I=ml212
Thus, we can write:
J⋅l2=I⋅ω
Substituting for I:
J⋅l2=ml212⋅ω
From the impulse equation, we can express ω:
J=mvcandJ=ml212⋅6vcl
This leads to:
ω=6vcl
The time t taken to complete one full revolution (where ωt=2π) can be expressed as:
t=2πω=2πl6vc=πl3vc
The distance xc traveled by the center of mass during this time can be calculated as:
xc=vc⋅t=vc⋅πl3vc=πl3
The center of mass translates a distance of:
πl3 while the rod completes one revolution about its center of mass.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct
142 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.3
21 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
Knowledge Check
The radius of gyration of an uniform rod of length l about an axis passing through one of its ends and perpendicular to its length is.
Al√2Bl3Cl√3Dl2
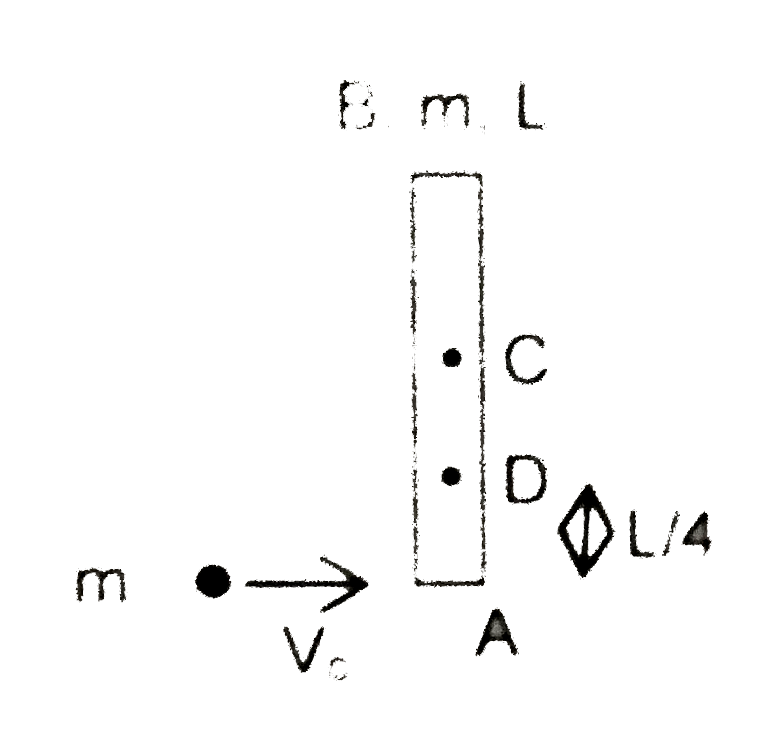
A thin, uniform rod of mass M and length L is at rest on a smooth horizontal surface. A particle of same mass M collides with the rod at one end perpendicular to its length with velocity V∘ and sticks to it. C is the middle point of the rod and D is a point at a distance of L/4 from end A. the time taken by the rod turn through 90∘ after collisions.
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionThe radius of gyration of a uniform rod of length l , about an axis passing through a point l8away form the centre of the rod , and perpendicular to it is:
View SolutionThe radius of gyration of a uniform rod of length l , about an axis passing through a point l8away form the centre of the rod , and perpendicular to it is:
View SolutionThe moment of inertia of a straight thin rod of mass M and length l about an axis perpendicular to its length and passing through its one end, is
View SolutionA thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is ω. Its centre of mass rises to a maximum height of -
View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View Solution