Initial angular velocity of a circular disc of mass M is ω1. Then two small spheres of mass m are attached gently to two diametrically opposite points on the edge of the disc. What is the final angular velocity of the disc -
(M+mM)ω1
(M+mm)ω1
(MM+4m)ω1
(MM+2m)ω1
The correct Answer is:C
To solve the problem of finding the final angular velocity of a circular disc after two small spheres are attached to it, we will use the principle of conservation of angular momentum.
1. Identify Initial Conditions:
- The initial angular velocity of the disc is ω1.
- The mass of the disc is M.
- The radius of the disc is R.
- The mass of each small sphere is m.
2. Calculate Initial Moment of Inertia:
- The moment of inertia I1 of the disc about its center is given by:
I1=12MR2
3. Determine the Moment of Inertia of the Spheres:
- When the two small spheres are attached to the disc, they are located at a distance R from the center. The moment of inertia I2 for one sphere is:
I2=mR2
- Since there are two spheres, the total moment of inertia contributed by the spheres is:
Ispheres=2⋅mR2=2mR2
4. Calculate Total Moment of Inertia After Spheres are Added:
- The total moment of inertia Itotal after adding the spheres is:
Itotal=I1+Ispheres=12MR2+2mR2
5. Apply Conservation of Angular Momentum:
- According to the conservation of angular momentum:
I1ω1=Itotalωfinal
- Substituting the values we have:
12MR2ω1=(12MR2+2mR2)ωfinal
6. Solve for Final Angular Velocity ωfinal:
- Rearranging the equation gives:
ωfinal=12MR2ω112MR2+2mR2
- Simplifying this expression:
ωfinal=Mω1M+4m
Final Answer:
Thus, the final angular velocity of the disc after the two small spheres are attached is:
ωfinal=MM+4mω1
- The initial angular velocity of the disc is ω1.
- The mass of the disc is M.
- The radius of the disc is R.
- The mass of each small sphere is m.
- The moment of inertia I1 of the disc about its center is given by:
I1=12MR2
- When the two small spheres are attached to the disc, they are located at a distance R from the center. The moment of inertia I2 for one sphere is:
I2=mR2
- Since there are two spheres, the total moment of inertia contributed by the spheres is:
Ispheres=2⋅mR2=2mR2
- The total moment of inertia Itotal after adding the spheres is:
Itotal=I1+Ispheres=12MR2+2mR2
- According to the conservation of angular momentum:
I1ω1=Itotalωfinal
- Substituting the values we have:
12MR2ω1=(12MR2+2mR2)ωfinal
- Rearranging the equation gives:
ωfinal=12MR2ω112MR2+2mR2
- Simplifying this expression:
ωfinal=Mω1M+4m
Thus, the final angular velocity of the disc after the two small spheres are attached is:
ωfinal=MM+4mω1
Topper's Solved these Questions
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (SINGLE OPTION CORRECT TYPE)
Explore 26 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (MULTIPLE OPTIONS CORRECT TYPE)
Explore 17 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:LEVEL - 2 (Angular Momentum, Collision)
Explore 20 Videos
- REVISION TEST-2 JEEBook:VMC MODULES ENGLISHChapter:REVISION TEST-2 JEEExercise:PHYSICS
Explore 25 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:7-previous year question
Explore 46 Videos
Similar Questions
Knowledge Check
A thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity ω. Two objects each of mass m are attached gently to the opposite ends of a diameter of the ring. The ring will now rotate with an angular velocity of
Aω(M−2m)(M+2m)BωM(M+2m)CωM(M+m)Dω(M+2m)MA thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity ω, Two objects, each of mass m, are attached gently to the opposite ends of a diameter of the ring. The wheel now rotates with an angular velocity ω=
AωMM+mBω(M−2m)M+2mCωMM+2mDω(M+2m)M
A thin circular ring of mass m and radius R is rotating about its axis perpendicular to the plane of the ring with a constant angular velocity ω. Two point particleseach of mass M are attached gently to the opposite end of a diameter of the ring. The ring now rotates, with an angular velocityω2. Then the ratiomM is
View SolutionA thin circular ring of mass M and radius R is rotating in a horizontal plane about an axis vertical to its plane with a constant angular velocity ω. If two objects each of mass m be attached gently to the opposite ends of a diameter of the ring, the ring will then rotate with an angular velocity
View SolutionA thin circular ring of mass M and radius R is rotating in a horizontal plane about an axis vertical to its plane with a constant angular velocity ω. If two objects each of mass m be attached gently to the opposite ends of a diameter of the ring, the ring will then rotate with an angular velocity
View SolutionA thin circular ring of mass M and radius R is rotating about its axis with an angular speed ω0 two particles each of mass m are now attached at diametrically opposite points. Find new angular speed of the ring.
View SolutionThe two uniform discs rotate separately on parallel axles. The upper disc (radius a and momentum of inertia I1) is given an angular velocity ω0 and the lower disc of (radius b and momentum of inertia I2) is at rest. Now the two discs are moved together so that their rims touch. Final angular velocity of the upper disc is.
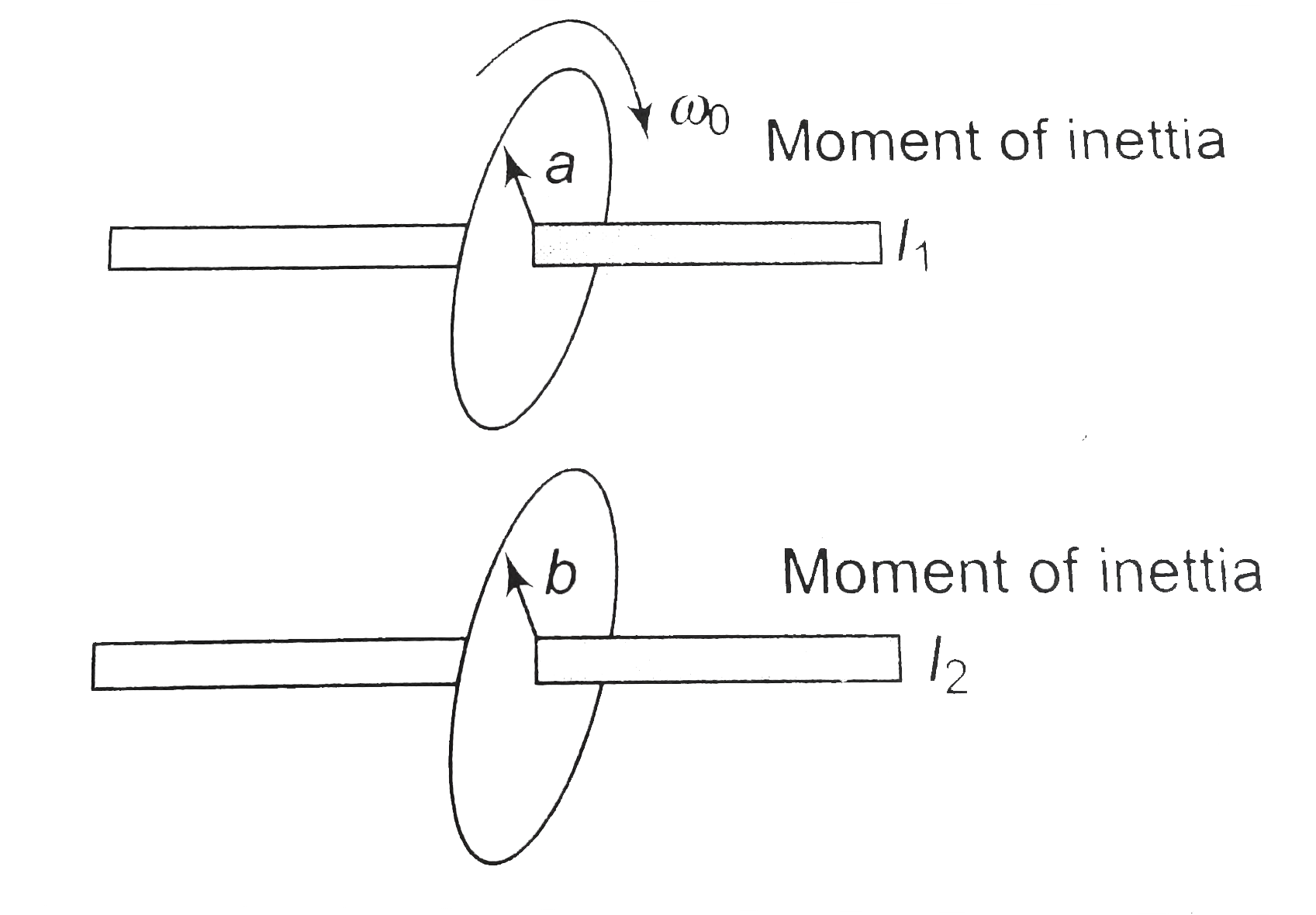 .
.
View SolutionA disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The angular speed of the disc when the balls reach the end of the disc is
View Solution
