The two uniform discs rotate separately on parallel axles. The upper disc (radius and momentum of inertia ) is given an angular velocity and the lower disc of (radius and momentum of inertia ) is at rest. Now the two discs are moved together so that their rims touch. Final angular velocity of the upper disc is.
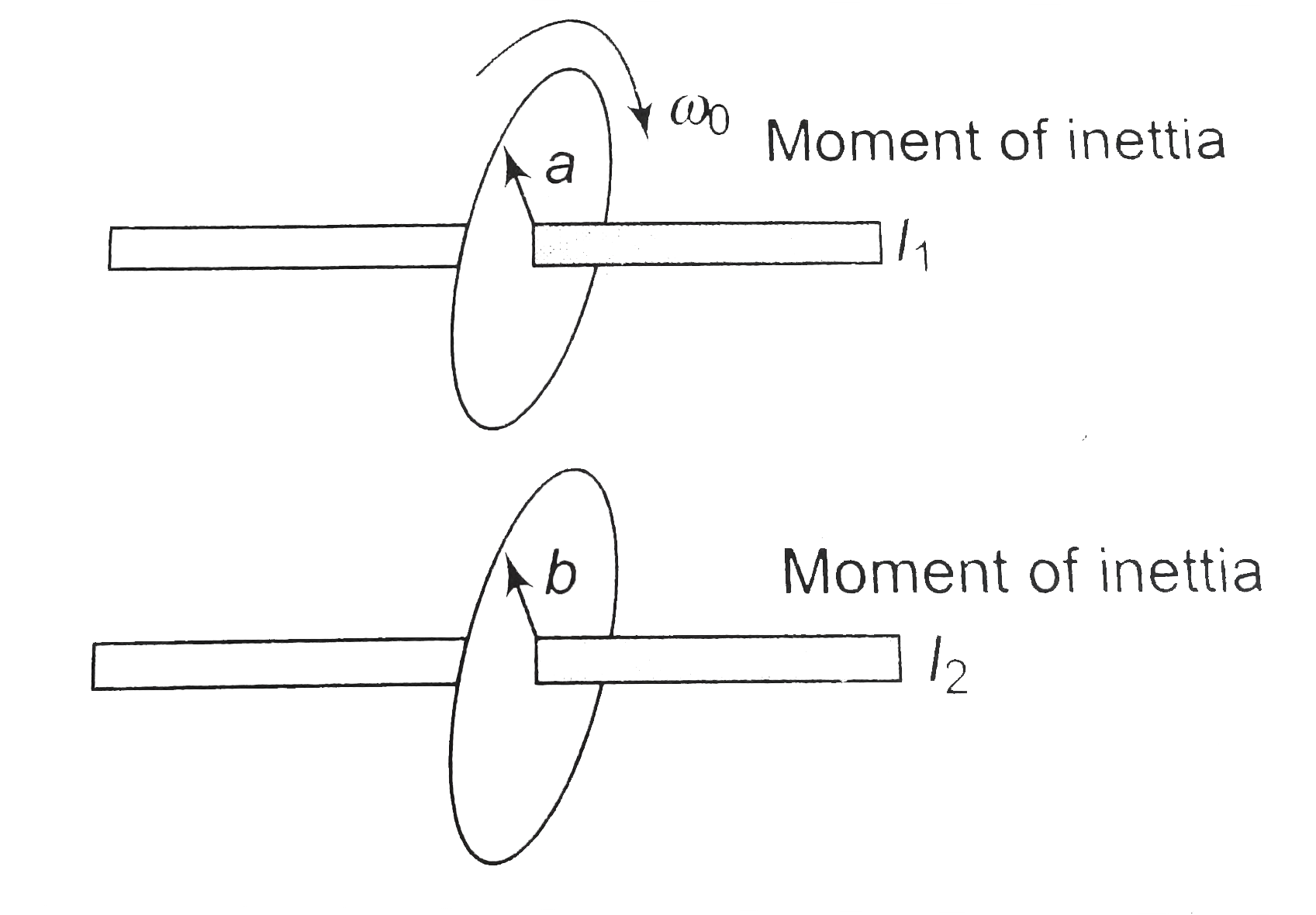 .
.
The two discs exert equal and opposite forces on each other when in contact. The torque due to these forces change the angular momentum of each disc. Form angular impulse angular momentum theorem, we have
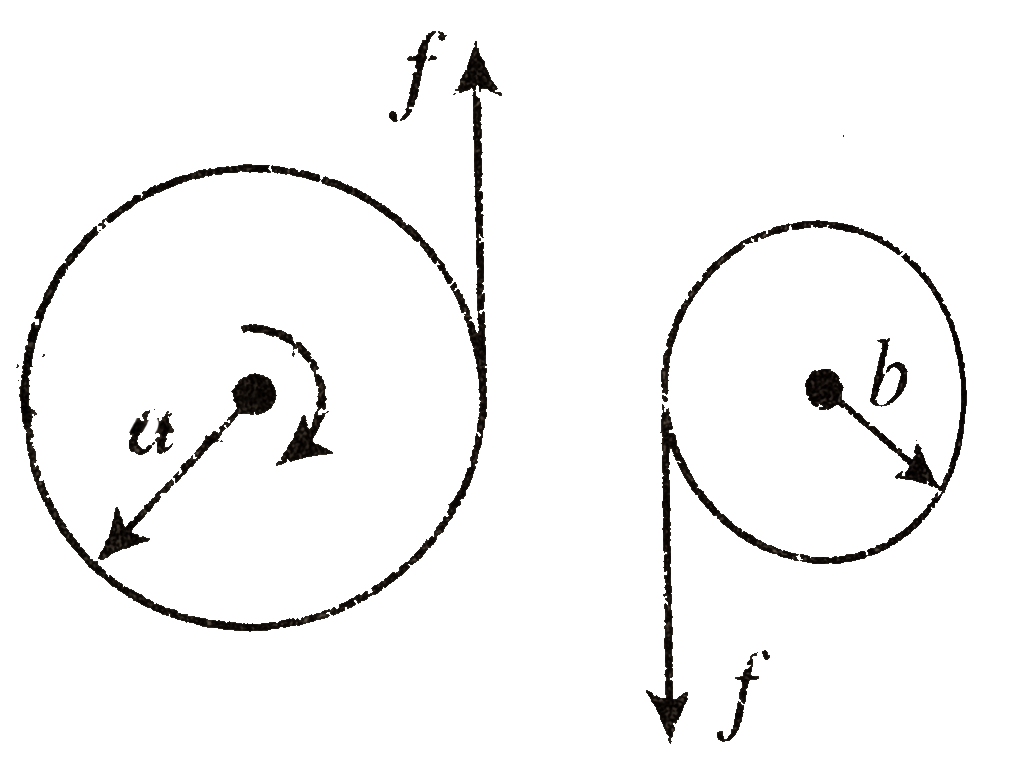
and
From eqn i and ii we get
When slipping ceaes between the disc, the contact points the two dics have the same linear velocity i.e.,
on substituting in eqn iii we get
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples12videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.111videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A round disc of moment of inertia I2 about its axis perpendicular to its plane and passing through its centre is placed over another disc of moment of inertia I1 rotating with an angular velocity ω about the same axis. The final angular velocity of the combination of discs is.
View SolutionInitial angular velocity of a circular disc of mass M is ω1. Then two small spheres of mass m are attached gently to two diametrically opposite points on the edge of the disc. What is the final angular velocity of the disc -
View Solution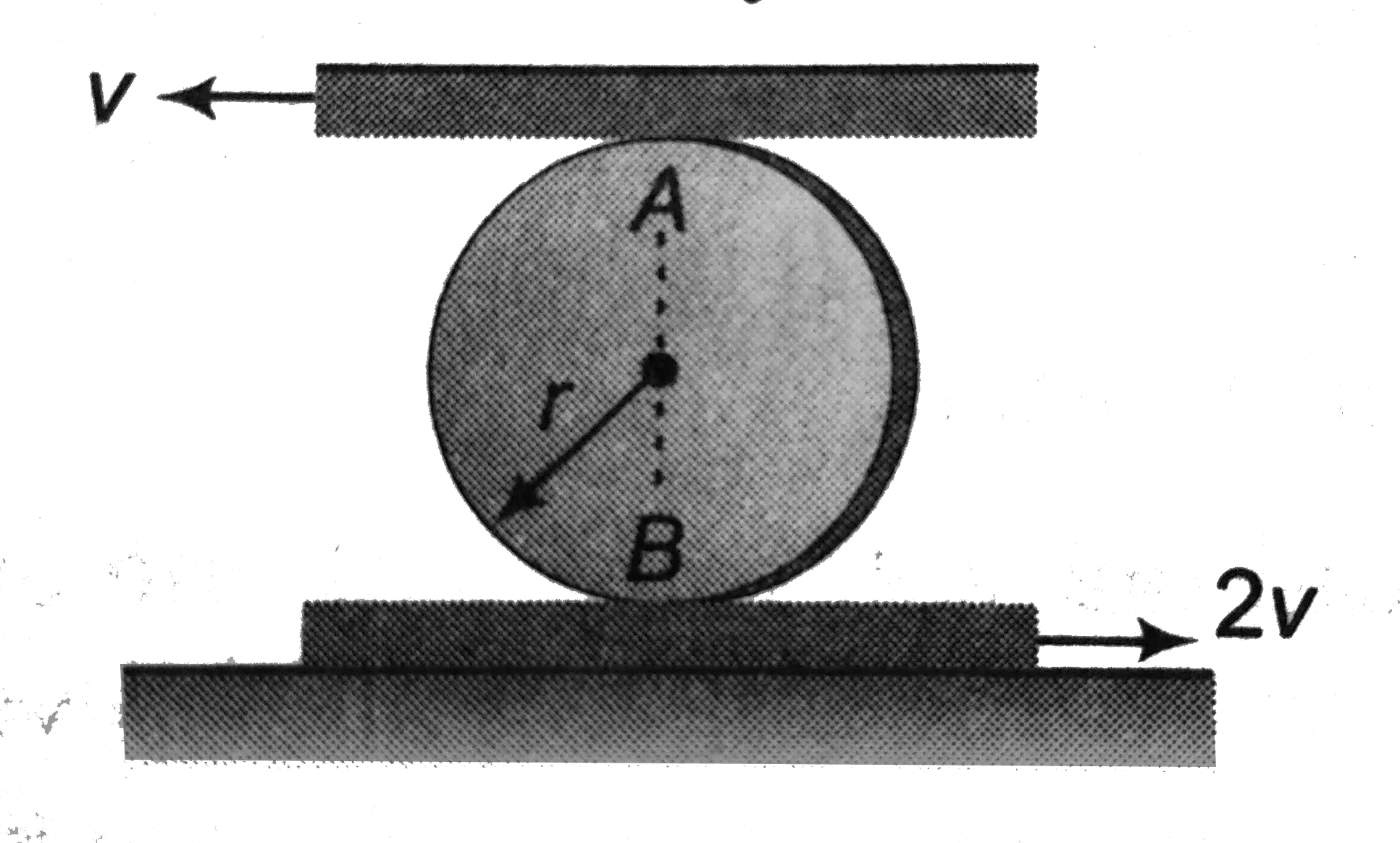
the disc of the radius r is confined to roll without slipping at A and B if the plates have the velocities shown, determine the angular velocity of the disc.View SolutionA disc is rotating with angular speed ω1. The combined moment of inertia of the disc and its axle is I1. A second disc of moment of inertia I2 is dropped on to the first and ends up rotating with it. Find the angular velocity of the combination if the original angular velocity of the upper disc was (a) zero (b) ω2 in the same direction as ω1 and (c) ω2 in a direction opposite to ω1.
View SolutionA disc with moment of inertia I is rotating with some angular speed. Second disc is initially at rest. Now second disc with moment of inertia 3I is placed on first disc and starts rotating. Find loss of kinetic energy in fraction
View SolutionA disc with moment of inertial I is rotating with some angular speed. Second disc is initially at rest. Now second disc with moment of inertia 3I is placed on first disc and starts rotating. Find loss of kinetic energy in fraction
View SolutionA disc of the radius R is confined to roll without slipping at A and B. If the plates have the velocities v and 2v as shown, the angular velocity of the disc is
 View Solution
View SolutionThe rotational kinetic energy of a disc is 450 J and its moment of inertia is 100 kg m2. What is its angular momentum ?
View SolutionTwo uniform circular rough disc of moment of inertia I1 and I12 are rotating with angular velocity ω1 and ω12 respectively in same direction. Now one disc is placed the other disc co-axially. The change in kinetic energy of the system is :
View SolutionA thin disc of radius R has charge Q distributed uniformly on its surface. The disc is rotated about one of its diametric axis with angular velocity ω. The magnetic moment of the arrangement is
View Solution
