A composite rod of mass 2m and length 2l comprises two indentica rods joined end to end at P. The composite rod hinged at one of its ends is kept horizontal as shown in the figure. If it is realeased from rest.
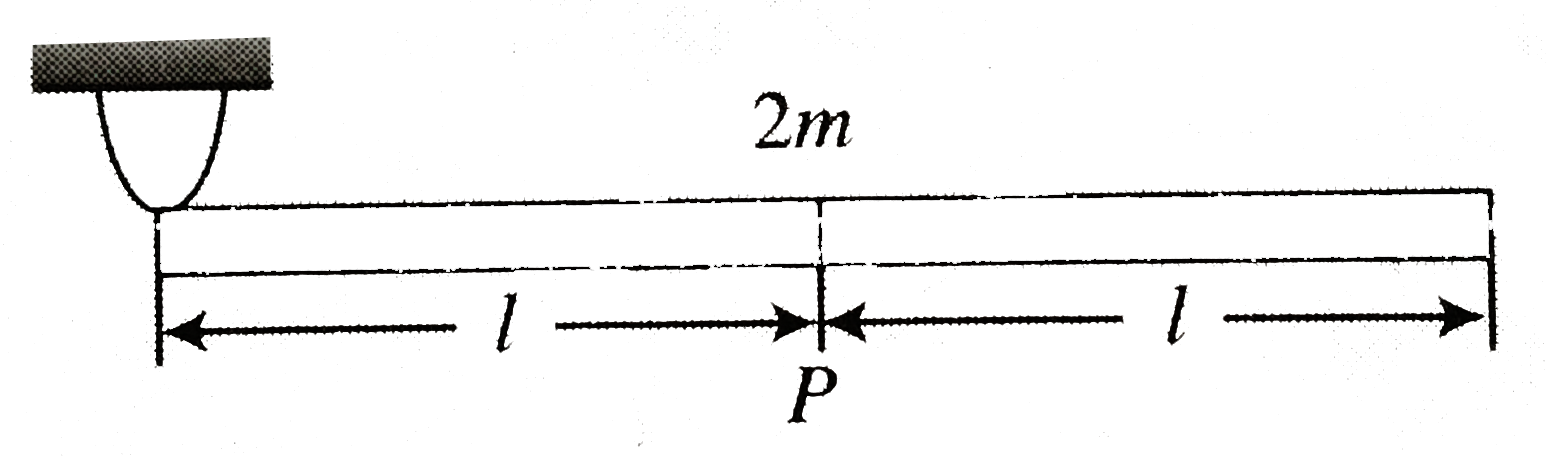
a. find its angular speed when it becomes vertical.
b. If the lower rod gets detached with the upper rod due to centrifugal effect at their joint P, at the vertical position of the composite rod, find their linear and angular velocities just after their separation.
a. Let the composite rod acquire an angular speed ωat the vertical position. It centre of mass C moves from C1 to C2.
Therefore the potential energy (gr) of the composite rod decreases by 2mgh where h=l. Applying conservation of mechanical energy at horizontal and vertical position.
Using △K+△K=(2m)gl

where l=MI of the composite rod about O=(2m)(2l)23=8ml23
⇒ω=√32gl
b. Referring to figure. we can see that just at the vertical position., during the impact, the weights of the component rods 1 and 2, the raction force R at the pivot and the reaction forces N at the joint of the rods, pass through the pivot O.
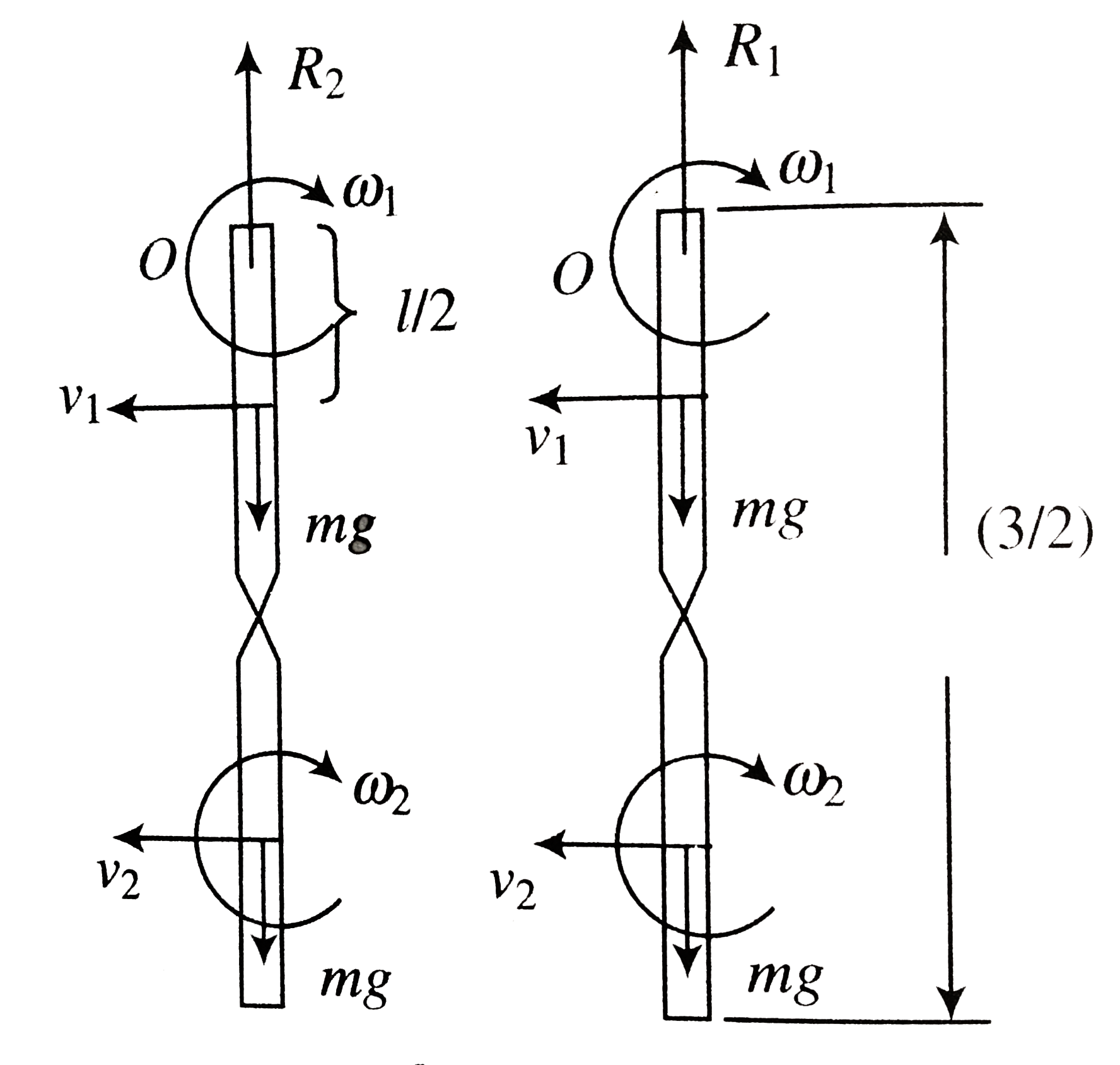
Therefore these forces cannot produce anny moment about O, that means the rods fo nt experience any horizontal force during breaking, at vertical position before the angular momentum of the system about O remains constant just after the breaking we can also argue that the angular momentum of each rod remains constant just before and after breaking. because all these radial forces cannot produce any moment about the centre of mass of the rods 1 and 2 vertical position. Therefore, the linear velocities of the CM of the rods remains constant.
⇒ω1=ω
v′1=v1=ωl2{for rod1}
ω2=ω
=v′2=v2=(32)ωl{for rod2}
⇒ωO1=ω2=√3g2l and v2=32√32gl
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.111videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.213videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in the figure. When string is cut, the initial angular accleration of the rod is.
 View Solution
View SolutionOne end of a uniform rod of length l and mass m is hinged at A. It is released from the rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes verticle is
 View Solution
View SolutionA rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionA rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the Horizontal component of the force applied by the hinge

View SolutionA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:
 View Solution
View SolutionA uniform rod of length l is from rest such that it rotates about a smooth pivot. The angular speed of the rod when it becomes vertical is.
 .View Solution
.View SolutionA rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the Normal reaction by ground on the rod

View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the intial angular acceleration of the rod is
 View Solution
View SolutionA thin rod of mass m and length l is hinged at the lower end to a level floor and stands vertically. Then its upper end will strike the floor with a velocity given by:
View SolutionA uniform rod of length 50 cm is released in the vertical plane from the position shown in the figure. The rod is hinged smoothly at O. The angular speed of rod when it becomes horizontal is ( take g=10ms−2 )
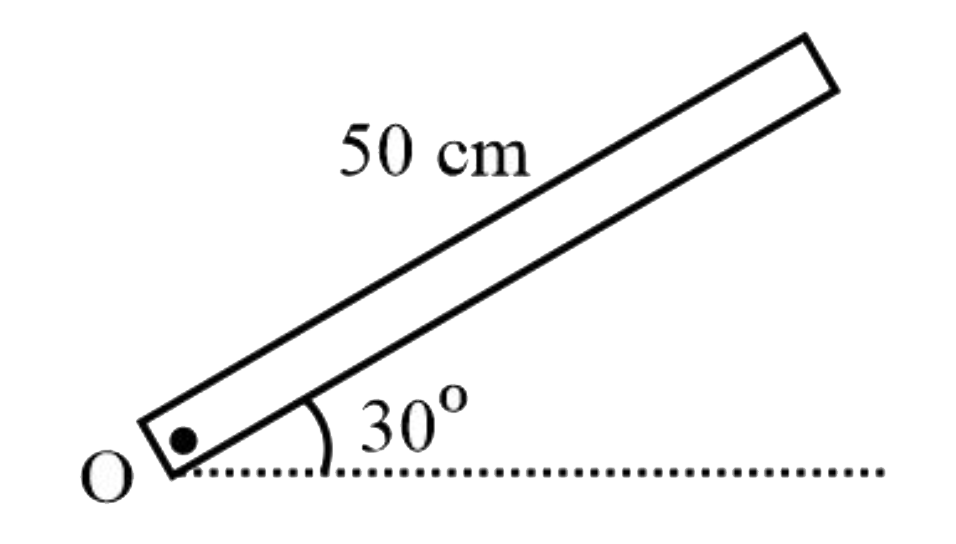 View Solution
View Solution

