A thin rod of mass m and length l is hinged at the lower end to a level floor and stands vertically. Then its upper end will strike the floor with a velocity given by:
√2gl
√3gl
√5gl
√mgl
The correct Answer is:B
To solve the problem of determining the velocity with which the upper end of a thin rod strikes the floor when it is hinged at the lower end and stands vertically, we can follow these steps:
1. Identify the System:
- We have a thin rod of mass m and length l that is hinged at one end and initially stands vertically.
2. Determine the Center of Mass:
- The center of mass of the rod is located at a distance of l2 from the hinge (the lower end).
3. Calculate Initial Potential Energy:
- The potential energy (PE) of the center of mass when the rod is vertical is given by:
PE=mgh=mg(l2)=mgl2
4. Determine the Moment of Inertia:
- The moment of inertia I of the rod about the hinge (lower end) is:
I=13ml2
5. Relate Kinetic Energy to Angular Velocity:
- When the rod falls, the potential energy converts into kinetic energy (KE). The kinetic energy of the rod when it is falling is given by:
KE=12Iω2=12(13ml2)ω2=ml2ω26
6. Apply Conservation of Energy:
- According to the conservation of energy, the initial potential energy equals the final kinetic energy:
mgl2=ml2ω26
7. Simplify the Equation:
- Cancel m from both sides:
gl2=l2ω26
- Rearranging gives:
gl=l2ω23
- Therefore:
ω2=3gl
8. Relate Angular Velocity to Linear Velocity:
- The linear velocity v of the upper end of the rod is related to the angular velocity ω by:
v=ωl
- Substituting ω:
v=l√3gl=√3gl
9. Final Result:
- The velocity with which the upper end of the rod strikes the floor is:
v=√3gl
- We have a thin rod of mass m and length l that is hinged at one end and initially stands vertically.
- The center of mass of the rod is located at a distance of l2 from the hinge (the lower end).
- The potential energy (PE) of the center of mass when the rod is vertical is given by:
PE=mgh=mg(l2)=mgl2
- The moment of inertia I of the rod about the hinge (lower end) is:
I=13ml2
- When the rod falls, the potential energy converts into kinetic energy (KE). The kinetic energy of the rod when it is falling is given by:
KE=12Iω2=12(13ml2)ω2=ml2ω26
- According to the conservation of energy, the initial potential energy equals the final kinetic energy:
mgl2=ml2ω26
- Cancel m from both sides:
gl2=l2ω26
- Rearranging gives:
gl=l2ω23
- Therefore:
ω2=3gl
- The linear velocity v of the upper end of the rod is related to the angular velocity ω by:
v=ωl
- Substituting ω:
v=l√3gl=√3gl
- The velocity with which the upper end of the rod strikes the floor is:
v=√3gl
Topper's Solved these Questions
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:LEVEL - 1 (Angular Momentum, Collision)
Explore 15 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:LEVEL - 1 (Mixed topics)
Explore 15 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:LEVEL-0 (LA: Long Answer Type)
Explore 3 Videos
- REVISION TEST-2 JEEBook:VMC MODULES ENGLISHChapter:REVISION TEST-2 JEEExercise:PHYSICS
Explore 25 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:7-previous year question
Explore 46 Videos
Similar Questions
A thin uniform rod AB of mass m and length l is hinged at one end to the level floor and stands vertically. If it s allowed to fall, with what angular velocity will it strike the floor?
View SolutionA rod of mass m and length l is lying on a horizontal table. Work done in making it stand on one end will be
View SolutionA uniform rod of mass m and length / is hinged at upper end. Rod is free to rotate in vertical plane. A bail of mass m moving horizontally with velocity vo collides at lower end of rod perpendicular to it and sticks to it. The minimum velocity of the ball such that combined system just completes the vertical circle will be
View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View SolutionA thin rod of length L and mass M is held vertically with one end on the floor and is allowed to fall. Find the velocity of the other end when it hits the floor, assuming that the end on the floor does not slip?
View SolutionA rod of mass m and length l hinged at the centre is placed on a horizontal surface. A bullet of mass m moving with velocity v strikes the end A of the rod and gets embedded in it. The angular velocity with which the systems rotates about its centre of mass after the bullet strikes the rod

View SolutionA rod of mass 4m and length L is hinged at the mid point. A ball of mass 'm' moving with speed V in the plane of rod, strikes at the end at an angle of 45∘ and sticks to it. The angular velocity of system after collision is-
View SolutionA rod of length 'l' is inclined at an angle 'θ' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1, what is the velocity of end B at the instant when rod makes 'θ' angle with the horizontal.
View SolutionA rod of uniform cross-section of mass M and length L is hinged about an end to swing freely in a vertical plane. Howerver, its density is non uniform and varies linearly from hinged end to the free end doubling its value. The moment of inertia of the rod, about the rotation axis passing through the hinge point
View SolutionIn the figure a uniform rod of mass 'm' and length 'l' is hinged at one end and the other end is connected to a light vertical of spring constant 'k' as shown in figure. The spring has extension such that rod is equilibrium when it is horizontal . The rod rotate about horizontal axis passing through end 'B'. Neglecting friction at the hinge find (a) extension in the spring (b) the force on the rod due to hinge.
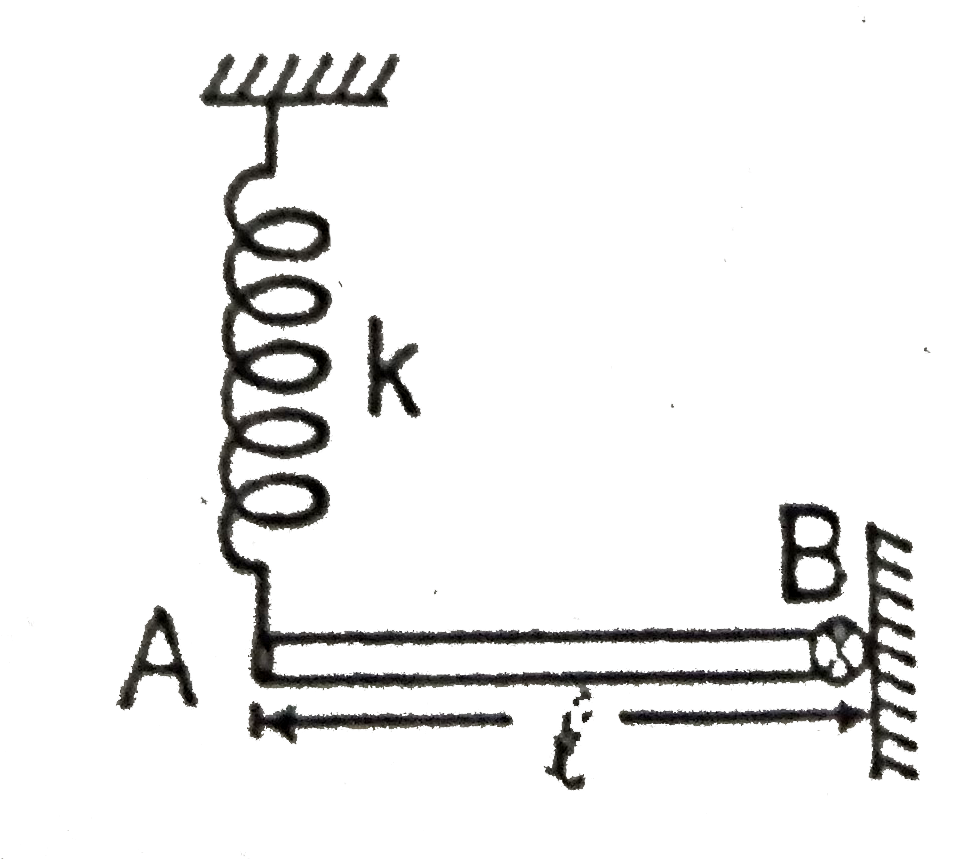
View Solution