A rod of length 'l' is inclined at an angle 'θ' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1, what is the velocity of end B at the instant when rod makes 'θ' angle with the horizontal.
To solve the problem, we need to analyze the motion of the rod and use the relationship between the velocities of its ends based on the geometry of the situation.
1. Understand the Geometry:
- We have a rod of length l inclined at an angle θ with the horizontal. Let point A be at the bottom of the rod (on the floor) and point B be at the top (against the wall).
- The vertical wall is smooth, meaning there is no friction acting on the rod at point B.
2. Identify the Variables:
- Let v1 be the velocity of end A (downward).
- Let v2 be the velocity of end B (horizontal).
3. Use the Pythagorean Theorem:
- The relationship between the horizontal and vertical distances can be expressed as:
x2+y2=l2
where x is the horizontal distance from point A to the wall, and y is the vertical distance from point A to point B.
4. Differentiate with Respect to Time:
- Differentiate the equation x2+y2=l2 with respect to time t:
2xdxdt+2ydydt=0
- This simplifies to:
xdxdt+ydydt=0
5. Substitute the Velocities:
- Substitute dxdt=v2 (the velocity of end B) and dydt=−v1 (the velocity of end A is downward):
xv2−yv1=0
- Rearranging gives:
v2=yxv1
6. Relate y and x Using Trigonometry:
- From the geometry of the situation, we know:
tan(θ)=yx
- Therefore, we can express yx as:
yx=tan(θ)
7. Final Expression for v2:
- Substitute yx back into the equation for v2:
v2=tan(θ)v1
Conclusion:
The velocity of end B when the rod makes an angle θ with the horizontal is given by:
v2=tan(θ)v1
- We have a rod of length l inclined at an angle θ with the horizontal. Let point A be at the bottom of the rod (on the floor) and point B be at the top (against the wall).
- The vertical wall is smooth, meaning there is no friction acting on the rod at point B.
- Let v1 be the velocity of end A (downward).
- Let v2 be the velocity of end B (horizontal).
- The relationship between the horizontal and vertical distances can be expressed as:
x2+y2=l2
where x is the horizontal distance from point A to the wall, and y is the vertical distance from point A to point B.
- Differentiate the equation x2+y2=l2 with respect to time t:
2xdxdt+2ydydt=0
- This simplifies to:
xdxdt+ydydt=0
- Substitute dxdt=v2 (the velocity of end B) and dydt=−v1 (the velocity of end A is downward):
xv2−yv1=0
- Rearranging gives:
v2=yxv1
- From the geometry of the situation, we know:
tan(θ)=yx
- Therefore, we can express yx as:
yx=tan(θ)
- Substitute yx back into the equation for v2:
v2=tan(θ)v1
The velocity of end B when the rod makes an angle θ with the horizontal is given by:
v2=tan(θ)v1
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - Application6videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - I157videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWER5videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)10videos
GEOMETRICAL OPTICS
- BOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)10videos
LOGIC GATES
Similar Questions
The block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal
 View Solution
View SolutionFigure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity v. Find the velocity of the other end B downward when the rod makes an angle θ with the horizontal.
 View Solution
View SolutionA rod of length l is moving in a vertical plane (x−y) when the lowest point A of the rod is moved with a velocity v. find the a angular velocity of the rod and b velocity of the end B.
 View Solution
View SolutionA uniform thin rod of mass m and length l is standing on a smooth horizontal suface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View SolutionA rod of length I leans by its upper end against a smooth vertical wall, while its other end leans against the floor. The end that leans against the wall moves uniformly downward. Then:
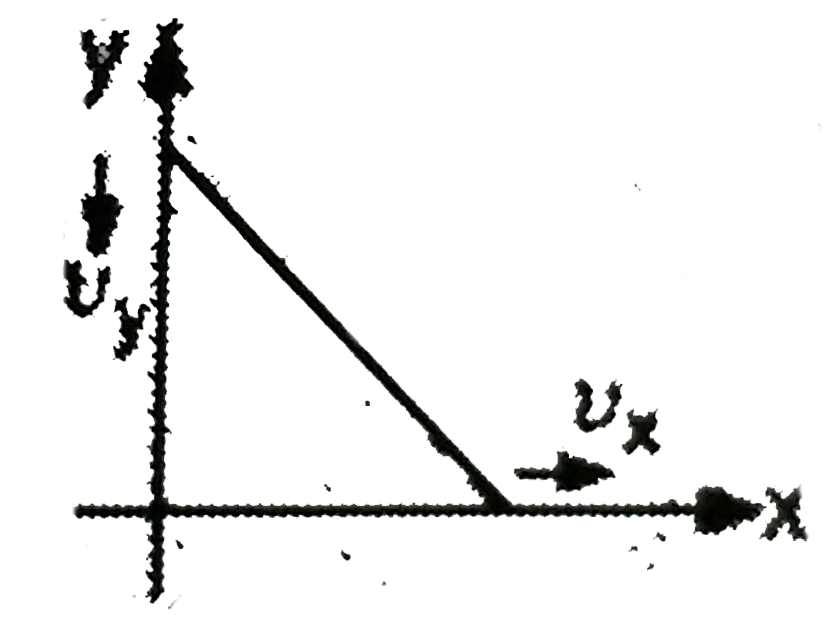 View Solution
View SolutionA thin rod of mass m and length l is hinged at the lower end to a level floor and stands vertically. Then its upper end will strike the floor with a velocity given by:
View Solution
A rod of length l forming an angle θ with the horizontal strikes a frictionless floor at A with its centre of mass velocity v0 and no angular velocity. Assuming that the impact at A is perfectly elastic. Find the angular velocity of the rod immediately after the impact.View SolutionA ladder of length L is slipping with its ends against a vertical wall and a horizontal floor. At a certain moment, the speed of the end in contact with the horizontal floor is v and the ladder makes an angle θ=30∘ with horizontal. Then, the speed of the ladder's centre of mass must be
View SolutionA rod AB is shown in figure. End A of the rod is fixed on the ground. Block is moving with velocity 2ms−1 towards right. The velocity of end B of rod at the instant shown in figure is
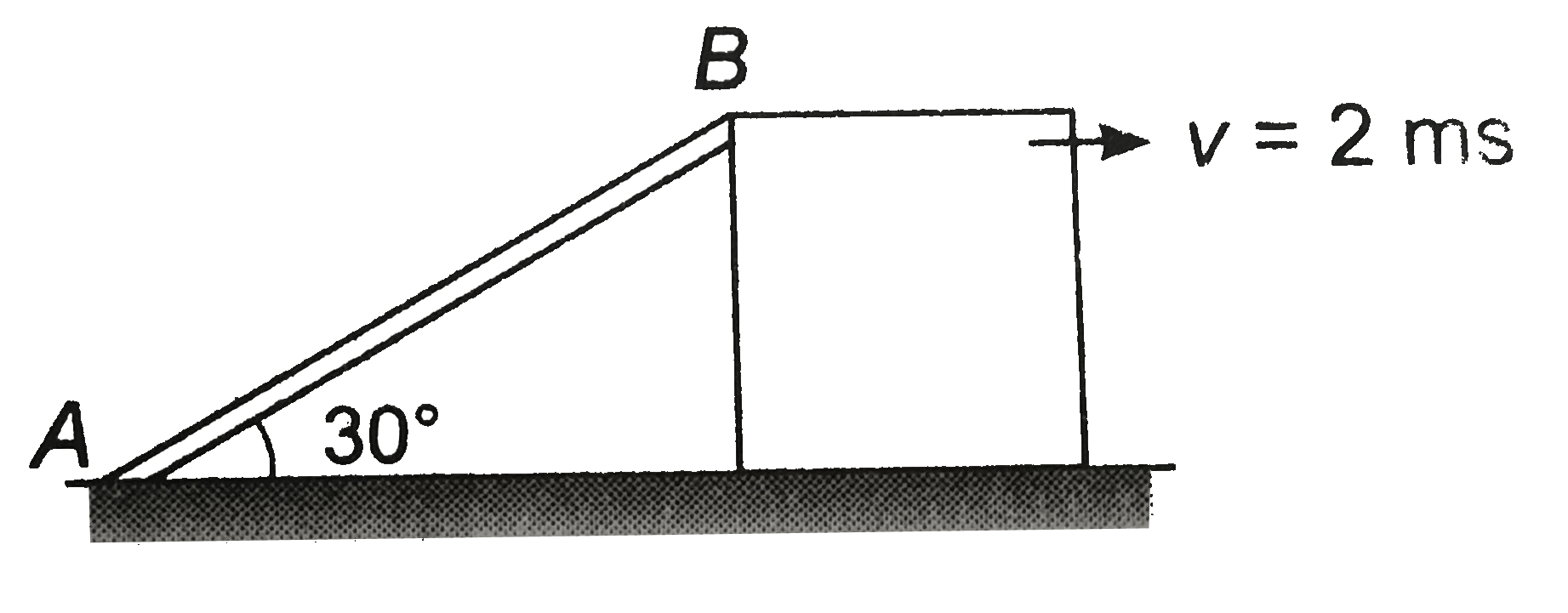 View Solution
View SolutionA man is walking under an inclined mirror at a constant velocity v along the x-axis. If the mirror is inclined at an angle θ with the horizontal then what is the velocity of the image ?
 View Solution
View Solution
