A thin rod of length L and mass M is held vertically with one end on the floor and is allowed to fall. Find the velocity of the other end when it hits the floor, assuming that the end on the floor does not slip?
Let M be the mass and L the length of the rod. When it is held vertically, its centre of mass is at a height (L2) from the floor, so that the potential energy of the stick is Mg (L/2). On releasing, the stick falls, i.e., it rotates about the end on the floor and 1 the potential energy is converted into rotational kinetic energy12ω2 , where I is the moment of inertia of the rod about the lower end and co the angular velocity when it hits the floor. Thus by conservation of mechanical energy,Mg=L2=12ω2 or Mg=L2=12ML23ω2[asI=1/3ML^2]oromega=sqrt(((3g)/L))Ifvisthel∈earvelocityoftheendhi∈gthe⌊,⌋thenv=rω=sqrt(3gL).
Topper's Solved these Questions
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES
20 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-1
4 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
Similar Questions
A meter stick is held vertically with one end on the floor and is allowed to fall. The speed of the other end when it hits the floor assuming that the end at the floor does not slip is (g=9.8m/s2)
View SolutionA thin rod of length L and mass M is held vertically with one end on the floor and is allowed to fall. Find the velocity of the other end when it hits the floor, assuming that the end on the floor does not slip?
View SolutionWhen a stick of length L mass M intially upright on a fricitionless floor starts falling the
View SolutionA rod of length l is moving in a vertical plane (x−y) when the lowest point A of the rod is moved with a velocity v. find the a angular velocity of the rod and b velocity of the end B.

View SolutionFigure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity v. Find the velocity of the other end B downward when the rod makes an angle θ with the horizontal.

View SolutionA uniform rod of length L and mass M is pivoted freely at one end and placed in vertical position.
a. What is angular acceleration of the rod when it is at ann angle θ with the vertical?
b. What is the tangential linear acceleration of the free end when the rod is horizontal?
View SolutionA thin rod of mass m and length l is hinged at the lower end to a level floor and stands vertically. Then its upper end will strike the floor with a velocity given by:
View SolutionA thin uniform rod AB of mass m and length l is hinged at one end to the level floor and stands vertically. If it s allowed to fall, with what angular velocity will it strike the floor?
View SolutionThe one end of a 20 m long ladder is on the floor and the other end is in the contact of vertical wall. Its lower end slides on the floor. Show that the rate of sliding of the upper end is 4/3 times the rate of sliding the lower end when the lower end is 16 m away from the wall.
View SolutionA rod of length L is sliding on a frictionless surface as shown in the figure. Velocity of end A is 4m/s along the wall. Find the velocity of end B, when end B makes 30∘ with wall PQ.
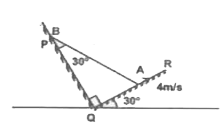
View Solution
