A constant horizontal force F is applied on the top of a solid sphere and a hallow sphere of same mass and radiuis both kept on a sufficiently rough surface. Let aS and aH be their linear acceleration respectively, then
aS=aH
aS>aH
aS<aH
data sufficient
The correct Answer is:B
To solve the problem, we need to analyze the motion of both the solid sphere and the hollow sphere under the influence of a constant horizontal force F. We will derive the linear accelerations aS for the solid sphere and aH for the hollow sphere step by step.
Step 1: Understand the Forces Acting on the Spheres
Both spheres are subjected to a constant horizontal force F applied at their tops. Additionally, there will be a frictional force f acting at the point of contact with the surface, opposing the motion.
Step 2: Write the Equation of Motion for the Solid Sphere
For the solid sphere, the net force acting on it can be expressed as:
F−f=maCM
where aCM is the linear acceleration of the center of mass of the solid sphere.
Step 3: Write the Torque Equation for the Solid Sphere
The torque τ about the center of the solid sphere due to the applied force F and the friction force f is given by:
τ=F⋅R−f⋅R
This torque is also related to the angular acceleration α of the sphere:
τ=Iα
For a solid sphere, the moment of inertia I is:
I=25mR2
Thus, we can write:
F⋅R−f⋅R=25mR2α
Step 4: Relate Linear and Angular Acceleration
For pure rolling motion, the linear acceleration aCM is related to the angular acceleration α by:
aCM=Rα
Substituting this into the torque equation gives:
F⋅R−f⋅R=25mR2(aCMR)
This simplifies to:
F−f=25maCM
Step 5: Substitute and Solve for Friction
Now we have two equations:
1. F−f=maCM
2. F−f=25maCM
From the first equation, we can express f:
f=F−maCM
Substituting this into the second equation:
F−(F−maCM)=25maCM
This simplifies to:
maCM=25maCM+F
Rearranging gives:
35maCM=F
Thus, the acceleration of the solid sphere is:
aS=5F3m
Step 6: Repeat for the Hollow Sphere
For the hollow sphere, the moment of inertia is:
I=23mR2
Following similar steps as above, we can derive:
F−f=maCM
And the torque equation becomes:
F⋅R−f⋅R=23mR2α
Using the relation aCM=Rα, we can derive:
F−f=23maCM
Solving this leads to:
aH=3Fm
Step 7: Compare the Accelerations
Now we have:
- aS=5F3m
- aH=3Fm
To compare aS and aH:
aS=5F3m<aH=3Fm
Conclusion
Thus, the linear acceleration of the solid sphere aS is less than that of the hollow sphere aH.
Both spheres are subjected to a constant horizontal force F applied at their tops. Additionally, there will be a frictional force f acting at the point of contact with the surface, opposing the motion.
For the solid sphere, the net force acting on it can be expressed as:
F−f=maCM
where aCM is the linear acceleration of the center of mass of the solid sphere.
The torque τ about the center of the solid sphere due to the applied force F and the friction force f is given by:
τ=F⋅R−f⋅R
This torque is also related to the angular acceleration α of the sphere:
τ=Iα
For a solid sphere, the moment of inertia I is:
I=25mR2
Thus, we can write:
F⋅R−f⋅R=25mR2α
For pure rolling motion, the linear acceleration aCM is related to the angular acceleration α by:
aCM=Rα
Substituting this into the torque equation gives:
F⋅R−f⋅R=25mR2(aCMR)
This simplifies to:
F−f=25maCM
Now we have two equations:
1. F−f=maCM
2. F−f=25maCM
f=F−maCM
Substituting this into the second equation:
F−(F−maCM)=25maCM
This simplifies to:
maCM=25maCM+F
Rearranging gives:
35maCM=F
Thus, the acceleration of the solid sphere is:
aS=5F3m
For the hollow sphere, the moment of inertia is:
I=23mR2
Following similar steps as above, we can derive:
F−f=maCM
And the torque equation becomes:
F⋅R−f⋅R=23mR2α
Using the relation aCM=Rα, we can derive:
F−f=23maCM
Solving this leads to:
aH=3Fm
Now we have:
- aS=5F3m
- aH=3Fm
aS=5F3m<aH=3Fm
Thus, the linear acceleration of the solid sphere aS is less than that of the hollow sphere aH.
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1 (Angular Momentum, Collision)
15 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1 (Mixed topics)
15 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL-0 (LA: Long Answer Type)
3 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
Torques of equal magnitude are applied to a thin hollow cylinder and a solid sphere, both having the same mass and radius. Both of them are free to rotate about their axis of symmetry. If αcandαs are the angular accelerations of the cylinder and the sphere respectively, then the ratio αcαs will be
View SolutionA solid sphere of mass M and radius R is pulled horizontally on a rough surface as shown in Fig. Choose the incorrect alternatives.

View SolutionA force (F=Mg) is applied on the top of a circular ring of mass M and radius R kept on a rough horizontal surface. If the ring rolls without slipping, then minimum coefficient of friction required is
_PHY_E05_236_Q01.png)
View Solution
Determine the maximum horizontal force F that may be applied to the plank of mass m for which the solid sphere does not slip as it begins to roll on the plank. The sphere has a mass M and radius R. The coefficient of static and kinetic friction between the sphere and the plank are μS and μk respectively.
View SolutionA constant horizontal force of 5N in magnitude is applied tangentially to the top most of a ring of mass 10 kg and radius 10 cm kept on a rough horizontal surface with coefficient of friction between surface and ring being 0.2. The friction force on the ring would be: (g=10m/s2)
View SolutionA force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:

View SolutionA solid sphere, a hollow sphere, a solid disc and a hollow cylinder are allowed to roll down a sufficiently rough inclined plane starting from rest. All have same mass and radius.

View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
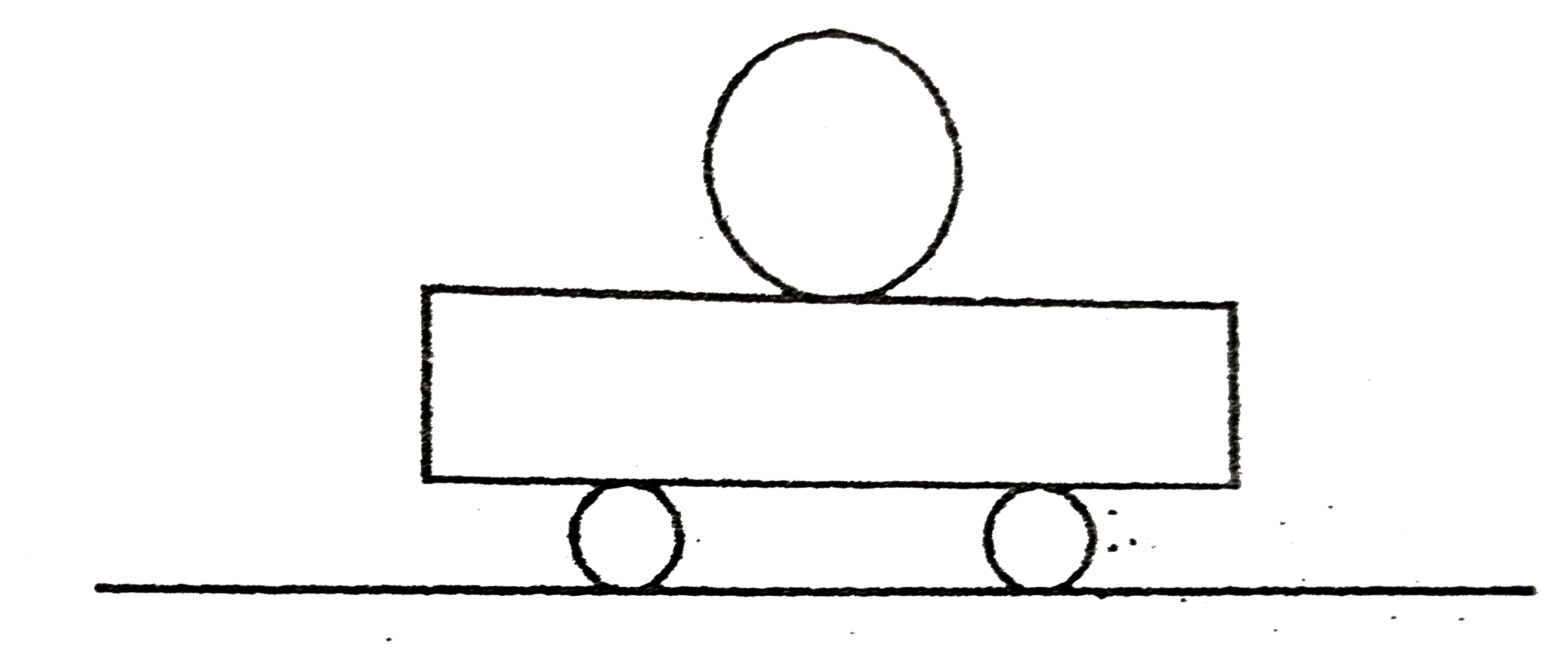
Angular acceleration of sphere is
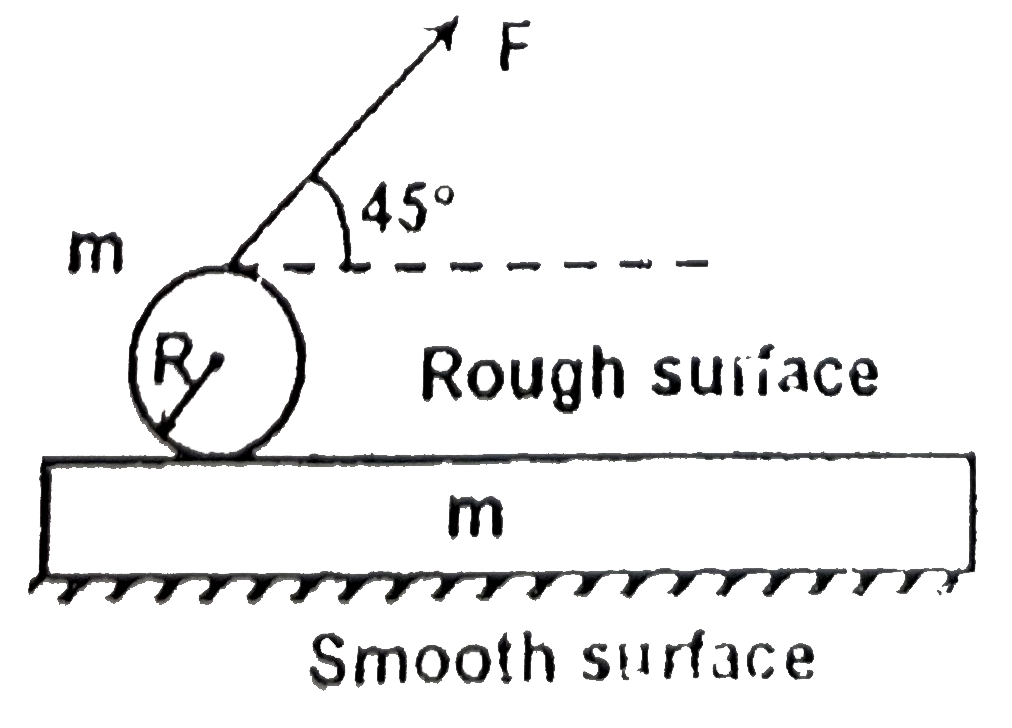
View SolutionA plank of mass m is placed on a smooth surface. Now, a uniform solid sphere of equal mass m and radius R is placed on the plank as shown in the figure. A force F is applied at topmost point of the sphere at an angle of 45∘ to the horizontal. Surface between the plank and the sphere is extremely rough so that there is no slip between the plank and the sphere. The force of firction acting between the plank and the sphere is Fk√2. Find the value of k.
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
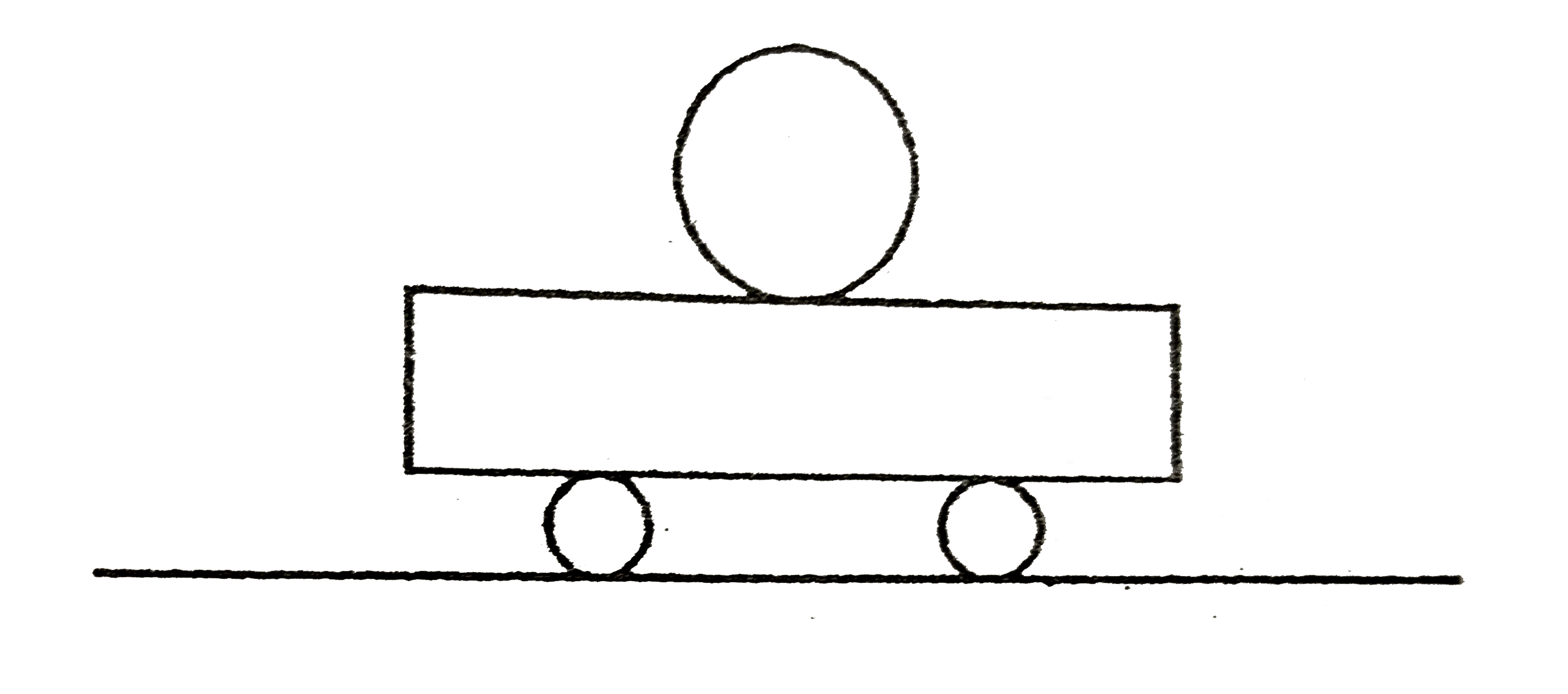
Acceleration of centre of mass of sphere is
View Solution
