A solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
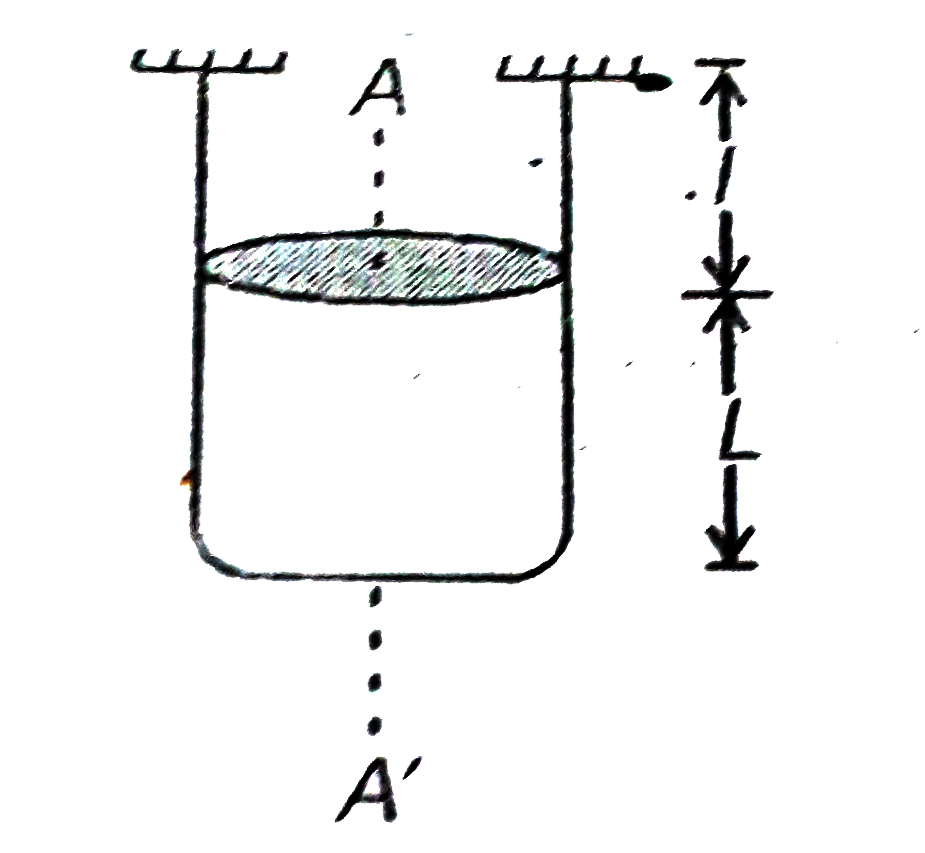
T=2π√R2g
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - EXAMPLE
21 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Exercise
18 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-I(SUBJECTIVE TYPE QUESTIONS) )
7 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
Similar Questions
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View Solution
A solid cylinder of mass M is attached to the spring by means of a frintionless pivot. The cylinder is placed on floor. Find the time period of small oscillation of the system, if the floor is sufficiently rought to prevent any slipping of cylinder. Assume stiffness of spring to be K.
View Solution
Knowledge Check
A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2
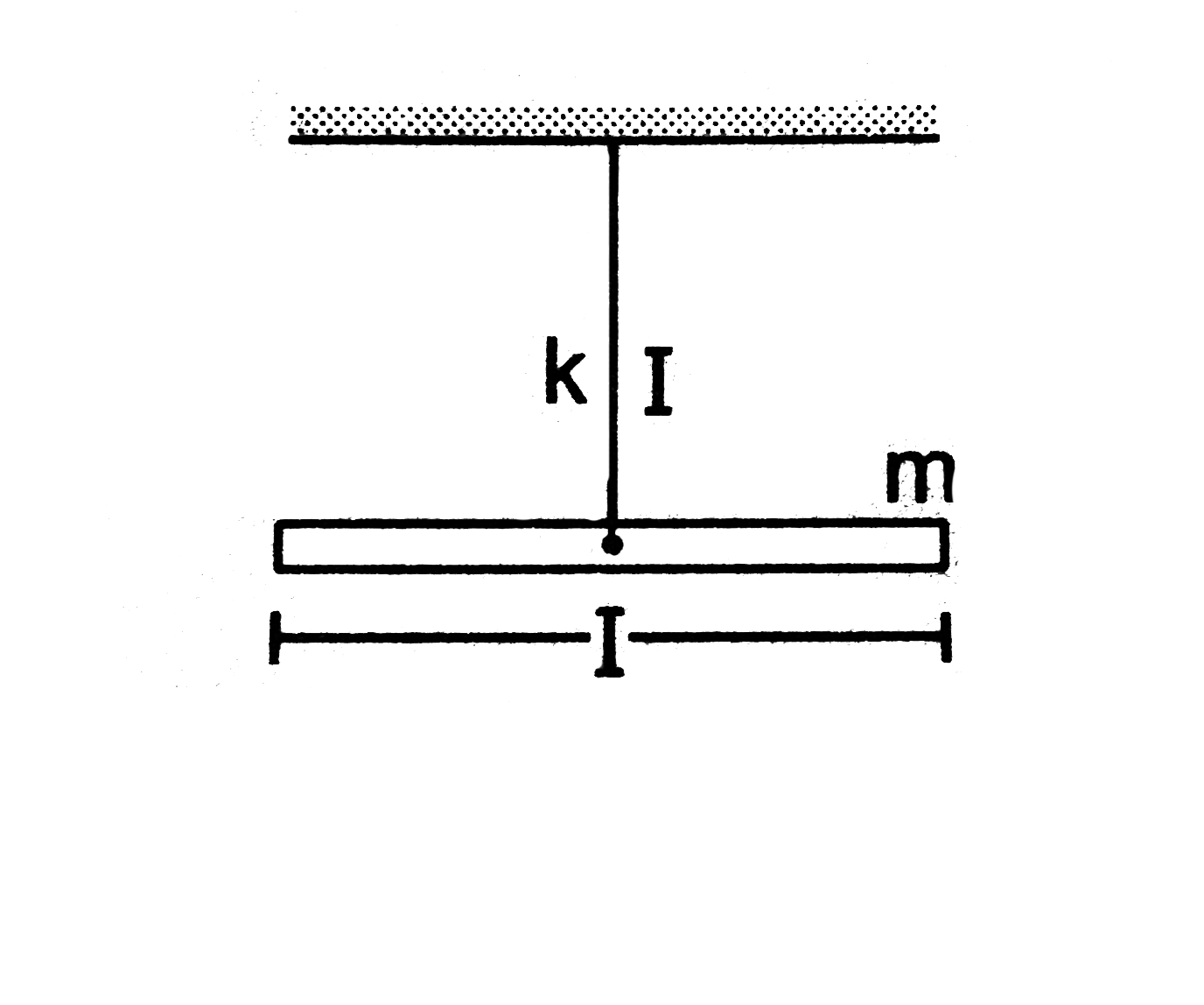
A uniform rod of mass m and length l is suspended through a light wire of length l and torsional constant k as shown in figure. Find the time perid iof the system makes a. small oscillations in the vertical plane about the suspension point and b. angular oscillations in the horizontal plane about the centre of the rod.
View SolutionA uniform solid sphere of mass m and radius R is suspended in vertical plane from a point on its periphery. The time period of its oscillation is
View SolutionThere is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
View SolutionA solid cylinder of mass M and radius R rolls without slipping down an inclined plane of length L and height h. What is the speed of its center of mass when the cylinder reaches its bottom
View SolutionThe moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I1 and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2
View SolutionA solid uniform cylinder of mass m performs small oscillations due to the action of two springs of stiffness k each (figure). Find the period of these oscillation in the absence of sliding.
x
View SolutionA solid cylinder of mass 20kg has length 1 m and radius 0.2 m. Then its moment of inertia (in kg-m2) about its geometrical axis is :
View Solution
