A mass of 0.5 kg is hung from a spring. A gradually increasing 0.5 N force is required to pull the mass downward a distance of 0.25 m from its equilibrium position,if the mass is then released from this position, find
(a) The total energy of the system .
(b) The frequency of the oscillation
(c ) The speed and acceleration of the mass as it passes the equilibrium position.
(d) The speed and acceleration of the mass when the diplacement from equilibrium is 0.25 m
(e) For the initial condition stated, write down the diplacement equation of motion for this mass.
Let's solve the problem step by step.
Given Data:
- Mass, m=0.5kg
- Force applied, F=0.5N
- Displacement from equilibrium, x=0.25m
- Acceleration due to gravity, g=10m/s2
Step 1: Calculate the spring constant k
From the equilibrium condition, the force due to the weight of the mass and the spring force balance each other:
mg=kx0
Where x0 is the initial extension of the spring.
When an additional force F is applied, the total downward force becomes:
mg+F=k(x0+x)
Substituting mg=kx0:
kx0+F=k(x0+x)
This simplifies to:
F=kx
Substituting the values:
0.5=k(0.25)
Thus,
k=0.50.25=2N/m
Step 2: Calculate the total energy of the system
The total energy E in a spring-mass system is given by:
E=12k(x0+x)2
We first need to find x0:
Using mg=kx0:
x0=mgk=0.5×102=2.5m
Now substituting k and x0:
E=12×2×(2.5+0.25)2=12×2×(2.75)2
Calculating:
E=1×7.5625=7.5625J
Step 3: Calculate the frequency of oscillation
The angular frequency ω is given by:
ω=√km=√20.5=√4=2rad/s
The frequency f is:
f=ω2π=22π=1πHz
Step 4: Speed and acceleration at the equilibrium position
At the equilibrium position, x=0:
- Acceleration a is given by:
a=−ω2x=−22⋅0=0m/s2
- Using conservation of energy, the total mechanical energy is equal to the kinetic energy at the equilibrium position:
E=12mv2
Substituting for E:
7.5625=12×0.5×v2
Solving for v:
v2=7.5625×20.5=30.25⟹v=√30.25≈5.5m/s
Step 5: Speed and acceleration at x=0.25m
At x=0.25:
- Velocity v=0 (at maximum displacement)
- Acceleration a:
a=−ω2x=−22⋅0.25=−1m/s2
Step 6: Displacement equation of motion
The displacement equation of motion for a simple harmonic oscillator is given by:
x(t)=Acos(ωt+ϕ)
Where:
- A=0.25m (amplitude)
- ϕ=π2 (since it starts from maximum displacement)
Thus, the equation becomes:
x(t)=0.25cos(2t+π2)=0.25sin(2t)
Summary of Answers:
(a) Total energy = 7.5625J
(b) Frequency = 1πHz
(c) Speed = 5.5m/s, Acceleration = 0m/s2
(d) Speed = 0m/s, Acceleration = −1m/s2
(e) Displacement equation = x(t)=0.25sin(2t)
- Mass, m=0.5kg
- Force applied, F=0.5N
- Displacement from equilibrium, x=0.25m
- Acceleration due to gravity, g=10m/s2
- Acceleration a:
- A=0.25m (amplitude)
- ϕ=π2 (since it starts from maximum displacement)
(a) Total energy = 7.5625J
(b) Frequency = 1πHz
(c) Speed = 5.5m/s, Acceleration = 0m/s2
(d) Speed = 0m/s, Acceleration = −1m/s2
(e) Displacement equation = x(t)=0.25sin(2t)
Topper's Solved these Questions
- OSCILLATIONSBook:AAKASH INSTITUTE ENGLISHChapter:OSCILLATIONSExercise:ASSIGNMENT ( SECTION-J )
Explore 8 Videos
- OSCILLATIONSBook:AAKASH INSTITUTE ENGLISHChapter:OSCILLATIONSExercise:EXAMPLE
Explore 21 Videos
- OSCILLATIONSBook:AAKASH INSTITUTE ENGLISHChapter:OSCILLATIONSExercise:ASSIGNMENT ( SECTION-H ( MULTIPLE TRUE-FALSE TYPE QUESTIONS) )
Explore 3 Videos
- NUCLEIBook:AAKASH INSTITUTE ENGLISHChapter:NUCLEIExercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
- PHYSICAL WORLDBook:AAKASH INSTITUTE ENGLISHChapter:PHYSICAL WORLDExercise:ASSIGNMENT (Section-B)
Explore 4 Videos
Similar Questions
Knowledge Check
A mass of 2kg is attached to the spring of spring constant 50Nm−1. The block is pulled to a distance of 5 cm from its equilibrium position at x=0 on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
Ax=0.05sin5t mBx=0.05cos5t mCx=0.5sin5t mDx=5sin5t m
A particle is attached to a vertical spring and is pulled down a distance 0.04m below its equilibrium position and is released from rest. The initial upward acceleration of the particle is 0.30ms−2. The period of the oscillation is
View SolutionGiven that the equation of motion of a mass is x=0.20sin(3.0t)m . Find the velocity and acceleration of the mass when the object is 5cm from its equilibrium position. Repeat for x=0.
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximum speed of the trolley is
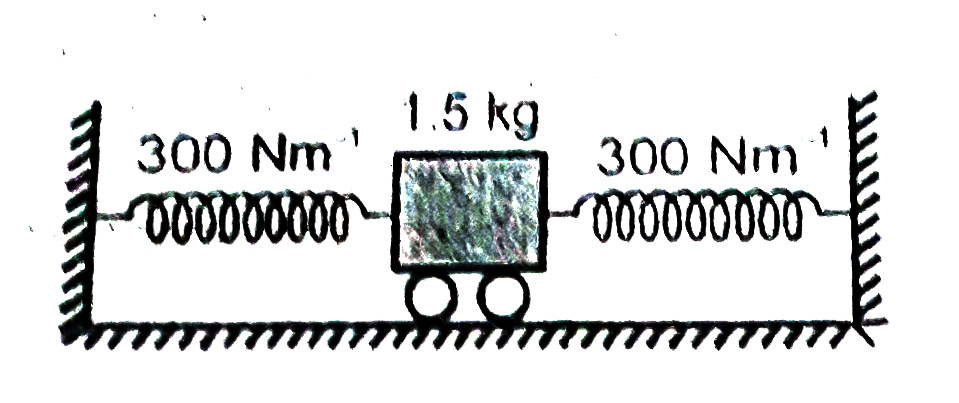
View SolutionA mass of 2kg is attached to the spring of spring constant 50Nm−1. The block is pulled to a distance of 5 cm from its equilibrium position at x=0 on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
View SolutionA particle is attached to a vertical spring and is pulled down a distance 4cm below its equilibrium and is released from rest. The initial upward acceleration is 0.5ms−2. The angular frequency of oscillation is
View SolutionA bob of mass m is suspended from the ceiling of a train moving with an acceleration a as shown in figure. Find the angle θ in equilibrium position.
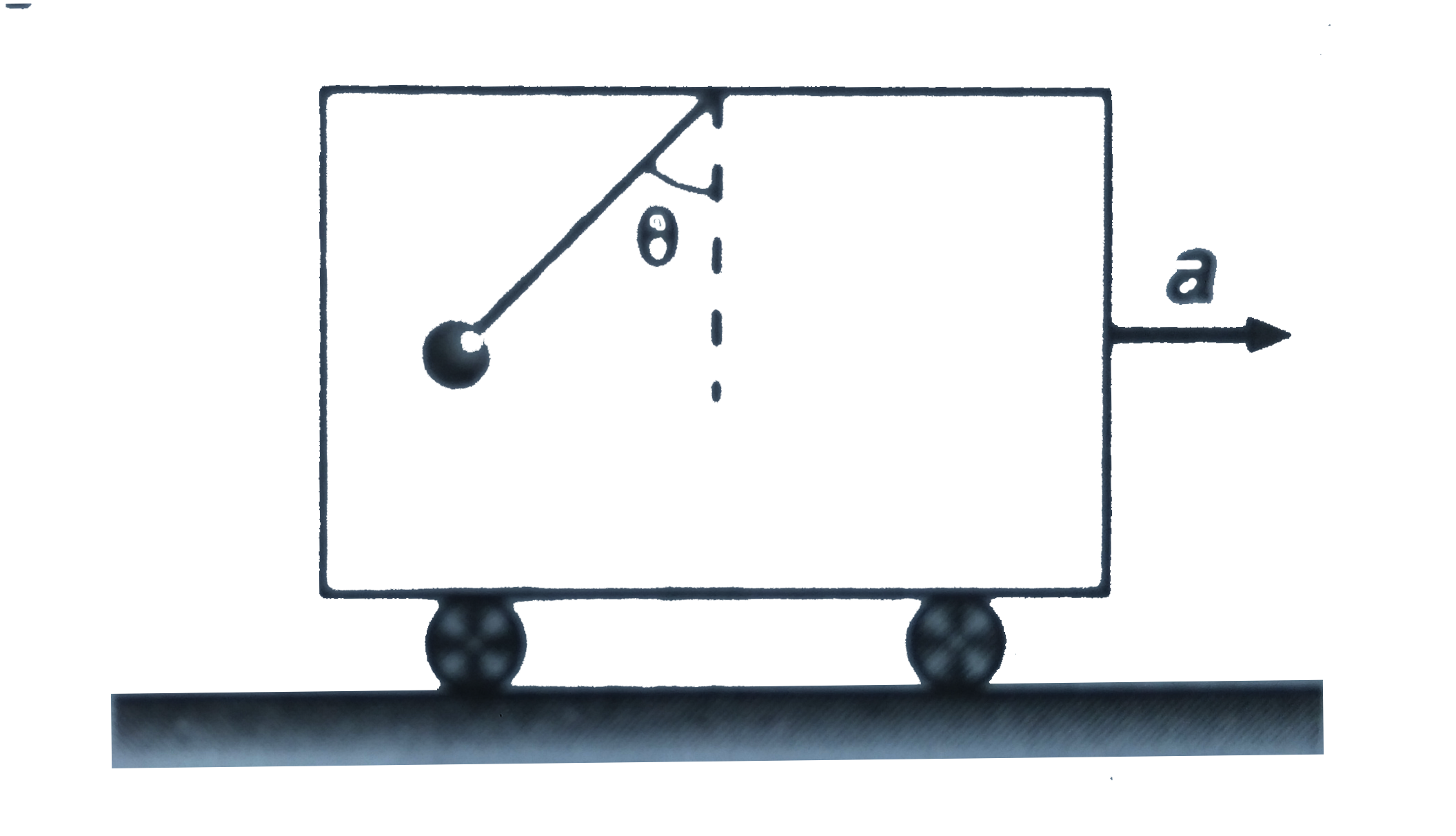
View Solution


