A particle is attached to a vertical spring and is pulled down a distance 0.04m below its equilibrium position and is released from rest. The initial upward acceleration of the particle is 0.30ms−2. The period of the oscillation is
4.08 s
1.92 s
3.90 s
2.29 s
The correct Answer is:D
To solve the problem step by step, we will follow the reasoning laid out in the video transcript.
Step 1: Understanding the Problem
A particle is attached to a vertical spring and is pulled down 0.04 m from its equilibrium position and released. The initial upward acceleration is given as 0.30 m/s². We need to find the period of oscillation of the particle.
Step 2: Relating Acceleration to Angular Frequency
The acceleration a of a particle in simple harmonic motion can be expressed as:
a=−ω2x
where ω is the angular frequency and x is the displacement from the equilibrium position. Since we are interested in the magnitude:
a=ω2x
Step 3: Substituting Known Values
From the problem, we know:
- a=0.30m/s2
- x=0.04m
Substituting these values into the equation:
0.30=ω2⋅0.04
Step 4: Solving for Angular Frequency ω
Rearranging the equation to solve for ω2:
ω2=0.300.04
Calculating the right side:
ω2=0.30×1000.04×100=304=7.5
Now, taking the square root to find ω:
ω=√7.5≈√302
Step 5: Finding the Time Period T
The period T of oscillation is given by the formula:
T=2πω
Substituting the value of ω:
T=2π√7.5=2π√30/2=4π√30
Step 6: Calculating the Numerical Value
Now we calculate T:
T=4×3.14√30≈12.565.477≈2.29s
Final Answer
Thus, the period of oscillation is approximately:
2.29s
A particle is attached to a vertical spring and is pulled down 0.04 m from its equilibrium position and released. The initial upward acceleration is given as 0.30 m/s². We need to find the period of oscillation of the particle.
The acceleration a of a particle in simple harmonic motion can be expressed as:
a=−ω2x
where ω is the angular frequency and x is the displacement from the equilibrium position. Since we are interested in the magnitude:
a=ω2x
From the problem, we know:
- a=0.30m/s2
- x=0.04m
0.30=ω2⋅0.04
Rearranging the equation to solve for ω2:
ω2=0.300.04
Calculating the right side:
ω2=0.30×1000.04×100=304=7.5
Now, taking the square root to find ω:
ω=√7.5≈√302
The period T of oscillation is given by the formula:
T=2πω
Substituting the value of ω:
T=2π√7.5=2π√30/2=4π√30
Now we calculate T:
T=4×3.14√30≈12.565.477≈2.29s
Thus, the period of oscillation is approximately:
2.29s
Similar Questions
A particle is attached to a vertical spring and is pulled down a distance 4cm below its equilibrium and is released from rest. The initial upward acceleration is 0.5ms−2. The angular frequency of oscillation is
View SolutionA mass of 0.5 kg is hung from a spring. A gradually increasing 0.5 N force is required to pull the mass downward a distance of 0.25 m from its equilibrium position,if the mass is then released from this position, find
(a) The total energy of the system .
(b) The frequency of the oscillation
(c ) The speed and acceleration of the mass as it passes the equilibrium position.
(d) The speed and acceleration of the mass when the diplacement from equilibrium is 0.25 m
(e) For the initial condition stated, write down the diplacement equation of motion for this mass.
View Solution
Knowledge Check
A particle moves such that its accleration a is given by a=−bx, where x is the displacement from equilibrium position and b is a constant. The period of oscillation is
A√2π/bB2π/√bC2π/bD2√(π/b)
A block of mass m=0.1kg is connected to a spring of unknown spring constant k. It is compressed to a distance x from its equilibrium position and released from rest. After approaching half the distance (x2) from the equilibrium position, it hits another block and comes to rest momentarily, while the other block moves with velocity 3ms−1. The total initial energy of the spring is :
View SolutionA mass m attached to a spring of spring constant k is stretched a distance x0 from its equilibrium position and released with no initial velocity. The maximum speed attained by mass in its subsequent motion and the time at which this speed would be attained are, respectively.
View SolutionA mass m attached to a spring of spring constant k is stretched a distance x0 from its equilibrium position and released with no initial velocity. The maximum speed attained by mass in its subsequent motion and the time at which this speed would be attained are, respectively.
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
What it is the time period of periodic motion of particle.
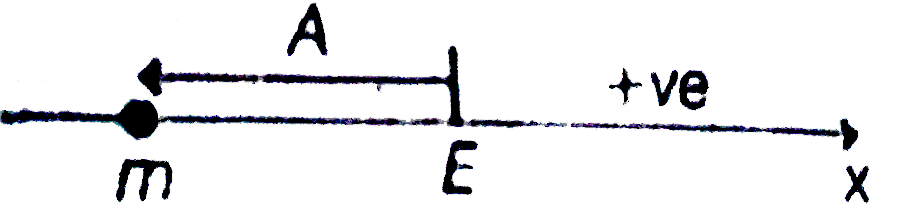
View SolutionA particle of mass m is rigidly attached at A to a ring of mass 3m and radius r. The system is released from rest and rolls without sliding. The angular acceleration of ring just after release is

View SolutionIn the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution

