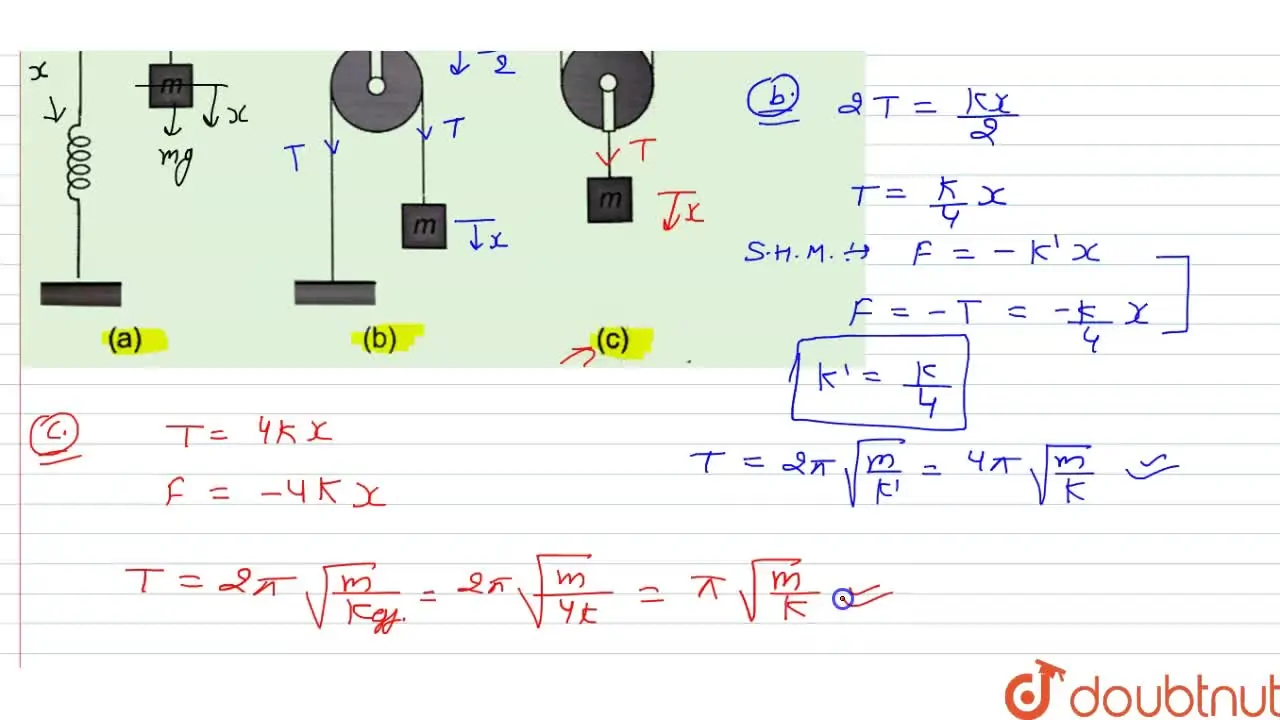
In the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.

(i) Let at some instant extension of spring is x, tension in the spring T=kx
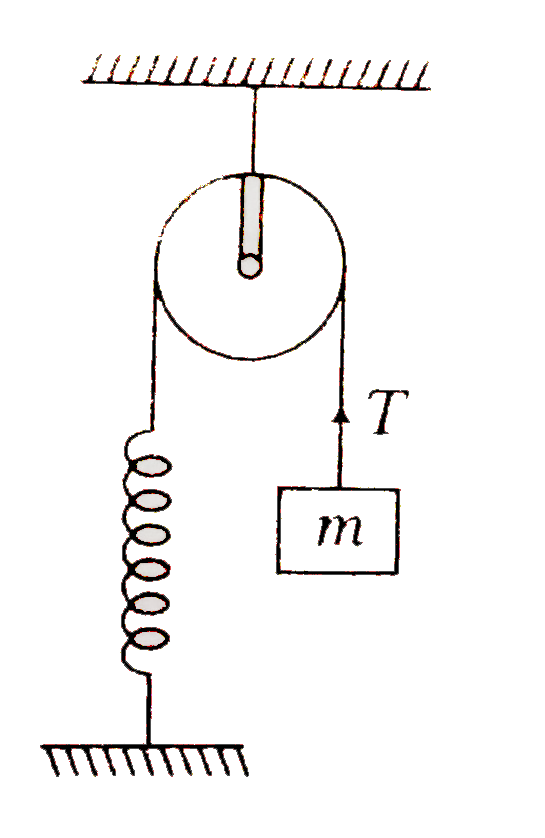
Restoring force , F=T=-kx (Hook's law)
where , k=spring constant
Time period ,
(ii) Let block move down by x, pulley will move by x/2.

Restoring force,
Comparing it with equation F=-kx
(iii) If block moves by x, pulley also moves x and hence spring is stretched by 2x.
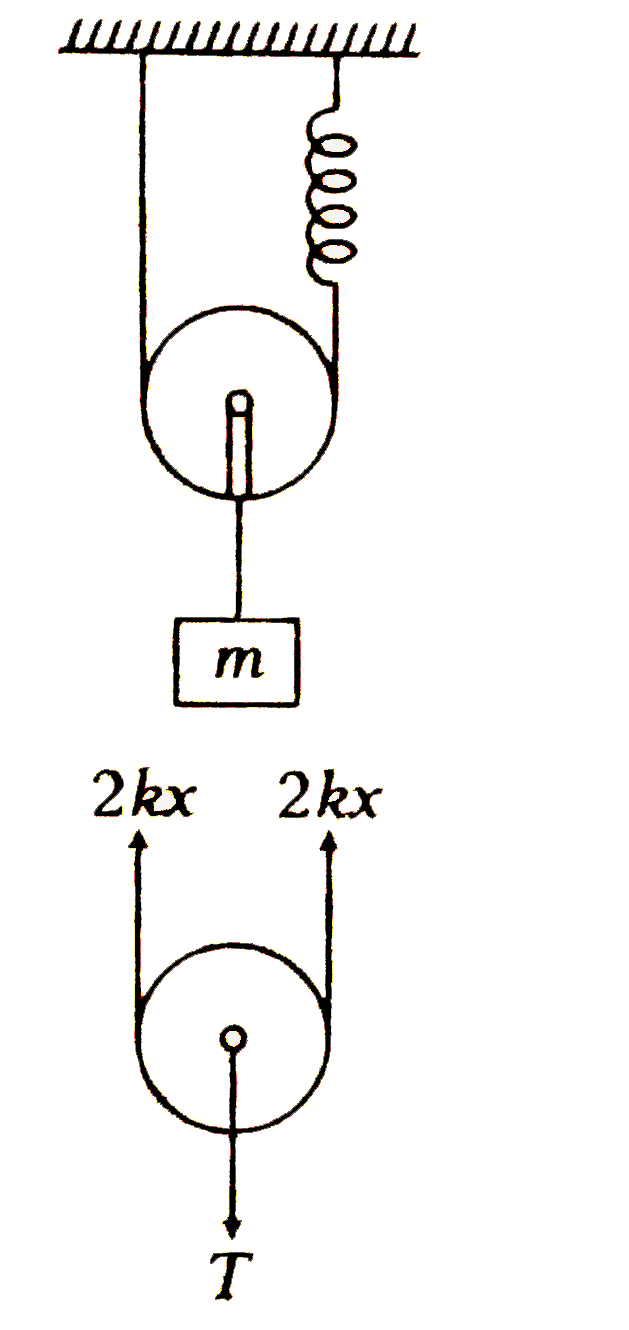
Tension produced in spring , T=4kx
Restoring force,
Comparing it with equation F=-k'x
we get k'=+4k
Similar Questions
Figure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
 View Solution
View SolutionFigure shows a system consisting of a massles pulley, a spring of force constant k and a block of mass m. If the block is sligthtly displaced vertically down from its equilibrium and released, find the period of its vertical oscillation in cases (a) and (b).
 View Solution
View SolutionA system shown in the figure consists of a massless pulley, a spring of force constant k displaced vertically downwards from its equilibrium position and released, then the Period of vertical oscillations is
 View Solution
View SolutionSpring mass system is shown in figure. find the time period of vertical oscillations. The system is in vertical plane.
 View Solution
View SolutionIn the figure shown, mass of the plank is m and that of the solid cylinder is 8m. Springs are light. The plank is slightly displaced from equilibrium and then released. Find the period of small oscillations (in seconds) of the plank. There is no slipping at any contact point. The ratio of the mass of the plank adn stiffness of the spring i.e., mK=2π2
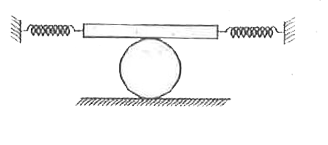 View Solution
View SolutionA 5 kg collar is attached to a spring of spring constant 500 N m−1. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10 cm and released. The time period of oscillation is
View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.
 View Solution
View SolutionA rectangular tank having base 15cm×20cm is filled with water (density ρ=1000kg/m3) up to 20cm and force constant K=280N/m is fixed to the bottom of the tank so that the spring remains vertical.
This system is in an elevator moving downwards with acceleration a=2m/s2. A cubical block of side l=10cm and mass m=2kg is gently placed over the spring and released gradually, as shown in the figure.

a. Calculate compression of the spring in equilibrium position.
b. If the block is slightly pushed down from equilibrium position and released, calculate frequency of its vertical oscillations.View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionConsider the plane of the paper to be vertical plane with direction of 'g' as shown in the figure. A rod (MM') of mass 'M' and carrying a current I. The rod is suspended vertically through two insulated spring of spring constant K at two ends. A uniform magnetic field is applied perpendicular to the plane of the paper such that the potential energy stored in the spring, in equilibrium position is zero. If the rod is slightly displaced in the vertically direction from the position of equilibrium, then the time period of oscillation is
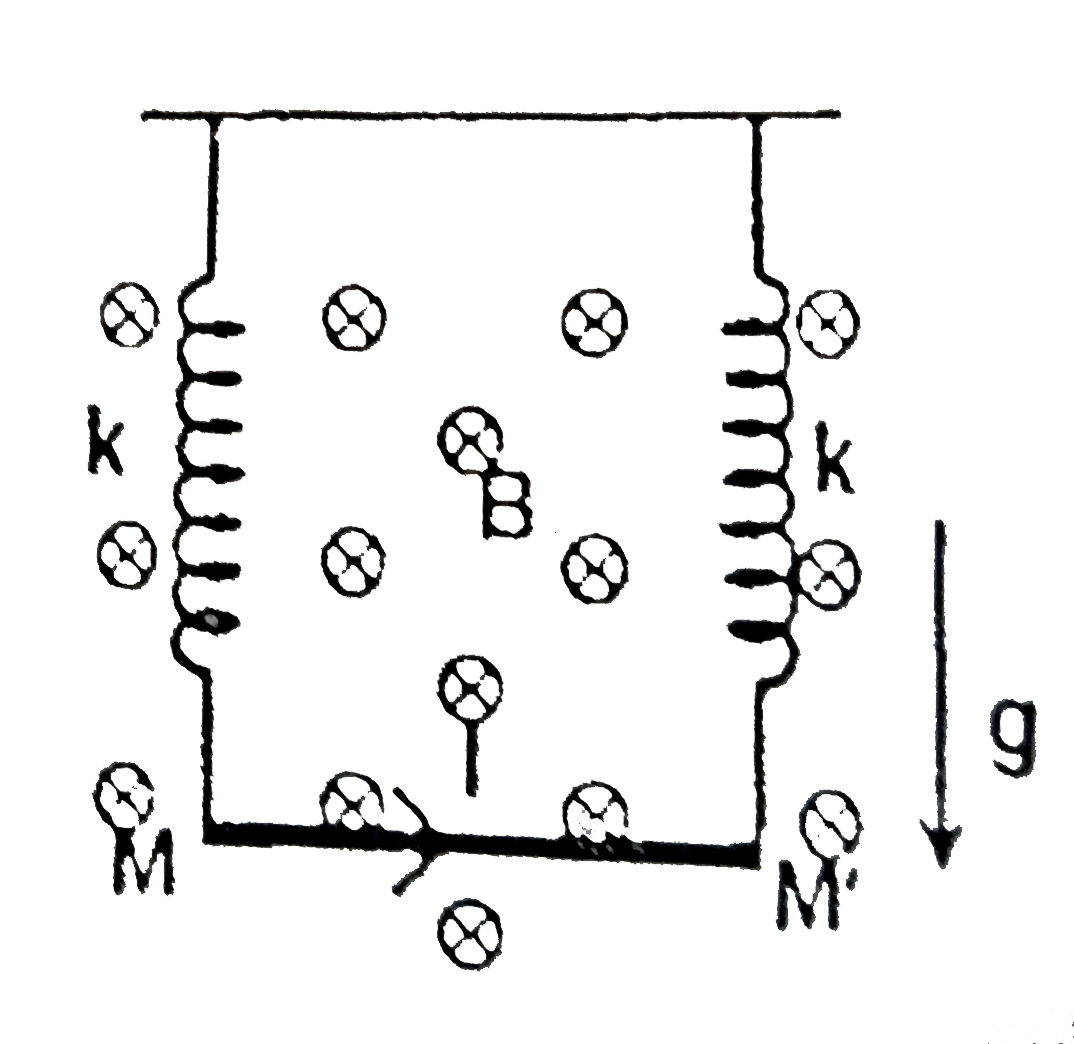 View Solution
View Solution