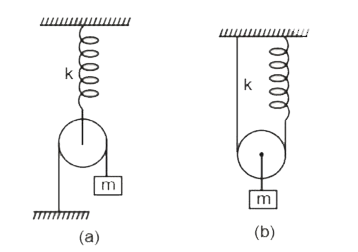
Figure shows a system consisting of a massles pulley, a spring of force constant k and a block of mass m. If the block is sligthtly displaced vertically down from its equilibrium and released, find the period of its vertical oscillation in cases (a) and (b).

The correct Answer is:A, B, D
(a) 
Two force are acting on the block :
(i) weight
(ii) tension
Weight is a constant force which does not contribute in time period. Tension is a variable force. Let tension increases by F when displaced from the equilibrium position by x. This increase in tension is the change in variable force. So, this is also the net restoring force. The distribution of this increase in tension F is as shown in figure.
Spring gets an extra stretching force 2F. Let x0 is the extra extension in the spring by this extra force 2F. Then,
2F=kx0
or x0=2Fk
Now, we can see that by this extra extension of spring, pulley will also come by the same distance x0 and
x=2x0=2(2Fk)
⇒F=k4x
But F is also the net restoring force on block. So, we can write
F=−(k4)x
∴T=2π√mk/4(aske=k/4)
=2π√4mk
(b) Using the same concepts as discussed above,
F2=kx0
or x0=F2k
But this time,
x0 = extra extension on spring.
= extra increase in length ABCD
=2x
or F2k=2x
or F=4kx
Due to the restoring nature of F we can write,
F=−(4k)x
∴T=2π√m4k(aske=4k)
 .
.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Miscellaneous Examples
Explore 8 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Level 1 Assertion And Reason
Explore 10 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Example Type 12
Explore 1 Video
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEYChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEYChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
Figure shows a system consisting of a massless pulley, a spring of force constant k and ablock of mass m. If the block is slightly displaced vertically down from its equillibrium position and then released, find the period of its vertical oscillation in cases (a) & (b).
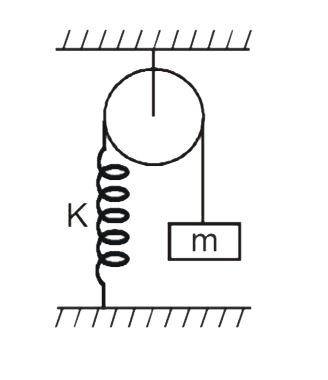
View SolutionFigure shows a system consisting of pulley having radius R, a spring of force constant k and a block of mass m. Find the period of its vertical oscillation.
View Solution
Knowledge Check
Figure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
 A2π√mKBπ√m4KCπ√mKD4π√mK
A2π√mKBπ√m4KCπ√mKD4π√mKThree springs of each force constant k are connected as shown figure. Point mass m is slightly displaced to compress A and released. Time period of oscillation is
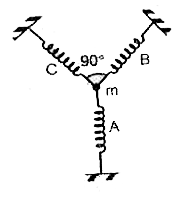 A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)
A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)An elastic string of constant k is attached to a block of mass m as shown. The block is given an extension of 2mgk from the equilibrium position and released. The time period of oscillations of the block is
 A2π√mkB4√mk(π3+√3)C2π√mk+2√3√mkDπ√mk+√3√mk
A2π√mkB4√mk(π3+√3)C2π√mk+2√3√mkDπ√mk+√3√mk
In the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.

View SolutionA system shown in the figure consists of a massless pulley, a spring of force constant k displaced vertically downwards from its equilibrium position and released, then the Period of vertical oscillations is

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionFind the period of a vertical spring - block system by both methods.
View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.

View Solution