Figure shows a system consisting of pulley having radius R, a spring of force constant k and a block of mass m. Find the period of its vertical oscillation.
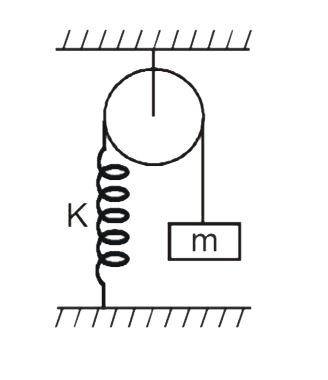
The following steps are usually followed in this method:
Step 1. Find the mean position. In following figure point A shows mean position.
Step 2. Write down the mean position force relation from figure.
mg = kx0
Step 3. Assume that particle is performing SHM with
amplitude A. Then displace the particle from its mean position.
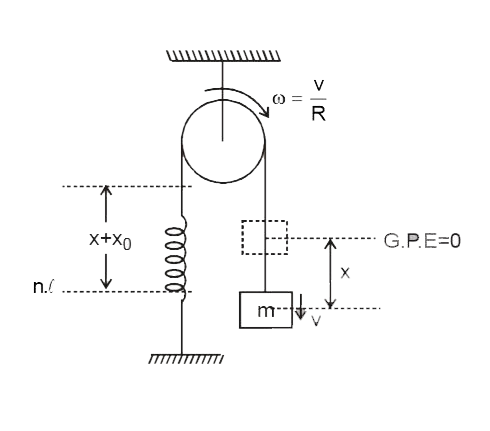
Step 4. Find the total mechanical energy (E) in the displaced position since, mechanical energy in SHM remains constant dEdt=0
E=12mv2+12Iω2+12k(x+x0)2 - mgx
E=12mv2+121v2R2+12k(x+x0)2-mgx
dEdt=2mv2dvdt+2Iv2R2dvdt+2k(x+x0)2dxdt
−mgdxdt ⋯(1)
Put dxdt=v and dvdt=d2xdt2
in eq. (1) put
dEdt=0
⇒mvd2xdt2+IvR2d2xdt2+kxv+kx0v−mgv=0
Which gives (m+1R2)d2xdt2+kx=0
d2xdt2+k(m+1R2)x=0 ⋯(2)
compare eq. (2) with S.H.M. eq. the
ω2=k(m+1R2)⇒T=2π√(m+1)/R2k
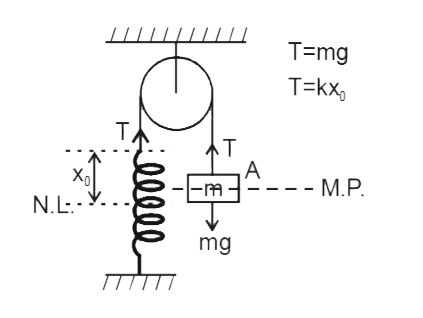
Topper's Solved these Questions
- SIMPLE HARONIC MOTION Book:MOTIONChapter:SIMPLE HARONIC MOTION Exercise:EXERCISE -1 ( SECTION-A )
Explore 8 Videos
- SIMPLE HARONIC MOTION Book:MOTIONChapter:SIMPLE HARONIC MOTION Exercise:EXERCISE -1 ( SECTION-B ) (Time per iod and angu larfrequency in SHM)
Explore 8 Videos
- SIMPLE HARMONIC MOTIONBook:MOTIONChapter:SIMPLE HARMONIC MOTIONExercise:EXERCISE -3 Section - B Previous Year Problems | JEE MAIN
Explore 23 Videos
- SOUND WAVESBook:MOTIONChapter:SOUND WAVESExercise:Exercise - 3 (Section - B)
Explore 14 Videos
Similar Questions
Figure shows a system consisting of a massles pulley, a spring of force constant k and a block of mass m. If the block is sligthtly displaced vertically down from its equilibrium and released, find the period of its vertical oscillation in cases (a) and (b).

View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and ablock of mass m. If the block is slightly displaced vertically down from its equillibrium position and then released, find the period of its vertical oscillation in cases (a) & (b).
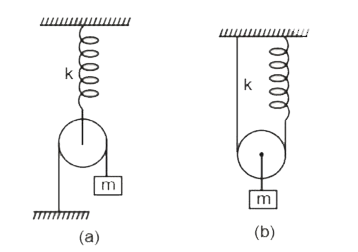
View Solution
Knowledge Check
Figure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
 A2π√mKBπ√m4KCπ√mKD4π√mK
A2π√mKBπ√m4KCπ√mKD4π√mKThe period of oscillation of a mass M, hanging from a spring of force constant k is T. When additional mass m is attached to the spring, the period of oscillation becomes 5T/4. m/M =
A9:16B25:16C25:9D16:9A particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mk
A system shown in the figure consists of a massless pulley, a spring of force constant k displaced vertically downwards from its equilibrium position and released, then the Period of vertical oscillations is

View SolutionAs shown in the figure a block of mass m is hung from the ceiling by the system of springs consisting of two layers. The force constant of each of the springs is k. The frequency of the vertical oscillations of the block is
View SolutionSpring mass system is shown in figure. Find the elastic potential energy stored in each spring when block is at its mean position. Also find the time period of vertical oscillations. The system is in vertical plane.

View SolutionSpring mass system is shown in figure. Find the elastic potential energy stored in each spring when block is at its mean position. Also find the time period of vertical oscillations. The system is in vertical plane.

View SolutionA block of mass m can slide along a frictionless inclined plane, is attached to a ideal spring of spring constant as shown in the figure. Find the period of its oscillation. (Frame of reference attached to the wedge is at rest)
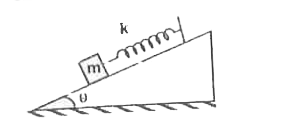
View Solution

