Figure shows a system consisting of a massless pulley, a spring of force constant k and ablock of mass m. If the block is slightly displaced vertically down from its equillibrium position and then released, find the period of its vertical oscillation in cases (a) & (b).
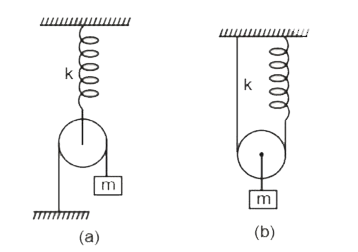
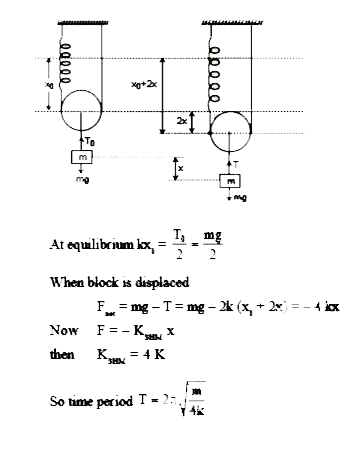
Let us assume that in equillibrium condition spring is x0 elongate from its natural length
In equilibrium T0=mgandkx0=2T0
⇒kx0=2mg ⋯(1)
If the mass m moves down a distance x from its equilibrium position then pulley will move down by x2 . So the extra force in spring will be kx2 . From figure Fnet=mg−T=mg−k2(x0+x2)
Fnet=mg−kx02−kx2
From eq. (1)
Fnet=−kx4 ⋯(3)
Now compare eq . (3) with F = - KS.H.Mx then KS.H.M=K4
⇒T=2πrT=2π√mKS.H.M.=2π√4mk

CASE (B) :
in this situiation of the mass m moves down distance x form its equilibrium position , then pulley will alspo move by x and so the spring will stetch by 2x .
Topper's Solved these Questions
- SIMPLE HARONIC MOTION Book:MOTIONChapter:SIMPLE HARONIC MOTION Exercise:EXERCISE -1 ( SECTION-A )
Explore 8 Videos
- SIMPLE HARONIC MOTION Book:MOTIONChapter:SIMPLE HARONIC MOTION Exercise:EXERCISE -1 ( SECTION-B ) (Time per iod and angu larfrequency in SHM)
Explore 8 Videos
- SIMPLE HARMONIC MOTIONBook:MOTIONChapter:SIMPLE HARMONIC MOTIONExercise:EXERCISE -3 Section - B Previous Year Problems | JEE MAIN
Explore 23 Videos
- SOUND WAVESBook:MOTIONChapter:SOUND WAVESExercise:Exercise - 3 (Section - B)
Explore 14 Videos
Similar Questions
Figure shows a system consisting of a massles pulley, a spring of force constant k and a block of mass m. If the block is sligthtly displaced vertically down from its equilibrium and released, find the period of its vertical oscillation in cases (a) and (b).

View SolutionFigure shows a system consisting of pulley having radius R, a spring of force constant k and a block of mass m. Find the period of its vertical oscillation.
View Solution
Knowledge Check
Figure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
 A2π√mKBπ√m4KCπ√mKD4π√mK
A2π√mKBπ√m4KCπ√mKD4π√mK
In the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.

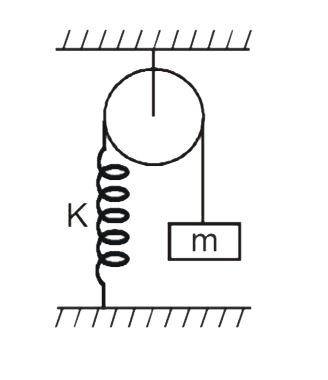
View SolutionA system shown in the figure consists of a massless pulley, a spring of force constant k displaced vertically downwards from its equilibrium position and released, then the Period of vertical oscillations is

View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionFind the time period of mass M when displaced from its equilibrium position and then reelased for the system shown in figure.
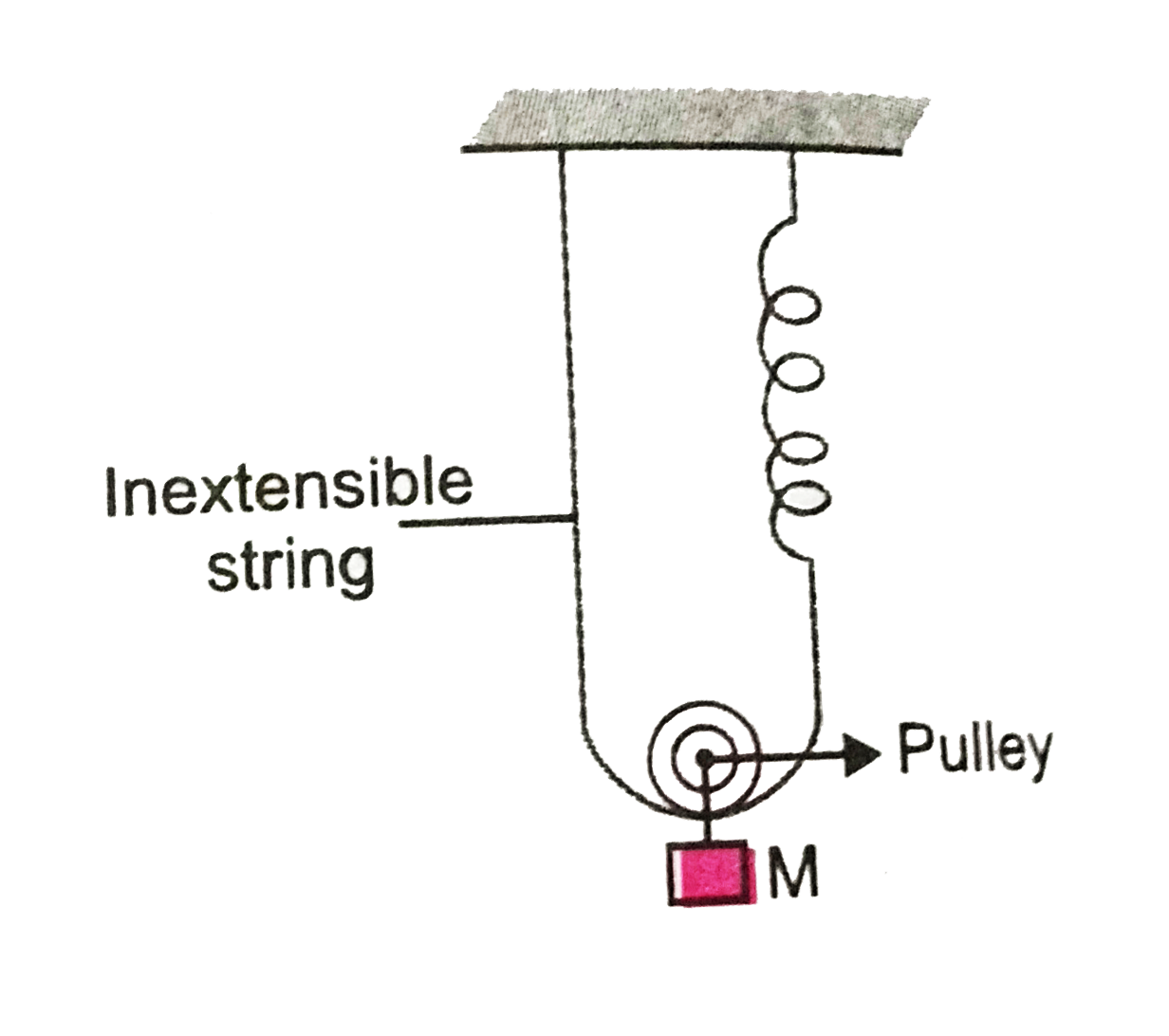
View SolutionOn applying a force F the mass M is displaced vertically down by from equilibrium position, Find the force F in terms of the force constant k of the spring and displacement y for the cases (A) and (B) as shown in
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.

View Solution

