On applying a force F the mass M is displaced vertically down by from equilibrium position, Find the force F in terms of the force constant k of the spring and displacement y for the cases (A) and (B) as shown in
Case (A) for the equilibrium of mass M
F=T …(i)
and for the equilibrium of pulley
2T=F' …(ii)
But as due to shift of mass M by y, the spring strentches by (y/2) so
F'=k(y/2) ….(iii)
So, substituting F' from Eqn. (iii) in Eqn. (ii) and then T from Eqn (ii) in Eqn. (i) we get
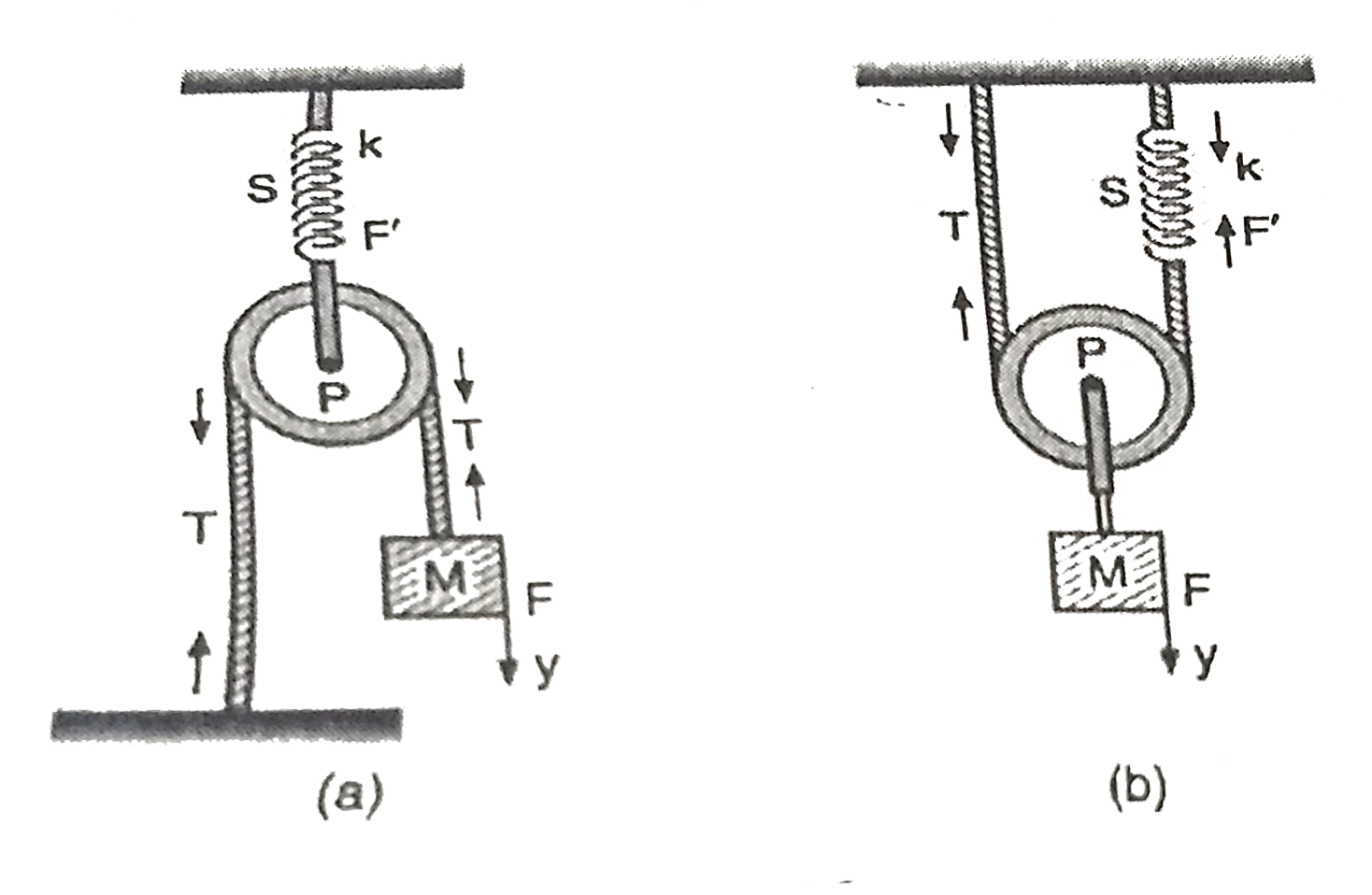
Case (B) As tension in massless string and spring will be same,
T=F'
And for equilibrium of pulley T+F'=F ...(i)
So, from Eqns (i) and (ii) F=2F' ....(ii)
Now if the mass M shifts by y the spring will stretch by 2y (as string is inextensible)
F'=k(2y) ....(iv)
So, subsituting f' from Eqn (iv) in Eqn (iii)
F=(4k)y ...(b)
Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Problem for practice
Explore 30 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Objective Questions
Explore 134 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Comprehension
Explore 12 Videos
- BASIC MATHEMATICSBook:GRB PUBLICATIONChapter:BASIC MATHEMATICSExercise:Problems For Practice
Explore 35 Videos
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Comprehension type
Explore 11 Videos
Similar Questions
On applying a force F, point P is displaced vertically down by y from equilibrium positionl. Find force F in terms of the force constant k of the spring and displacement y, for the cases (a) and (b), as shown in fig.

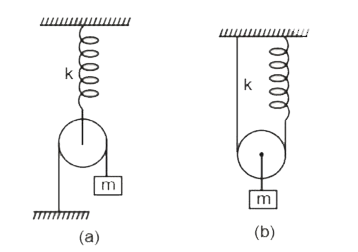
View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and ablock of mass m. If the block is slightly displaced vertically down from its equillibrium position and then released, find the period of its vertical oscillation in cases (a) & (b).
View Solution
Knowledge Check
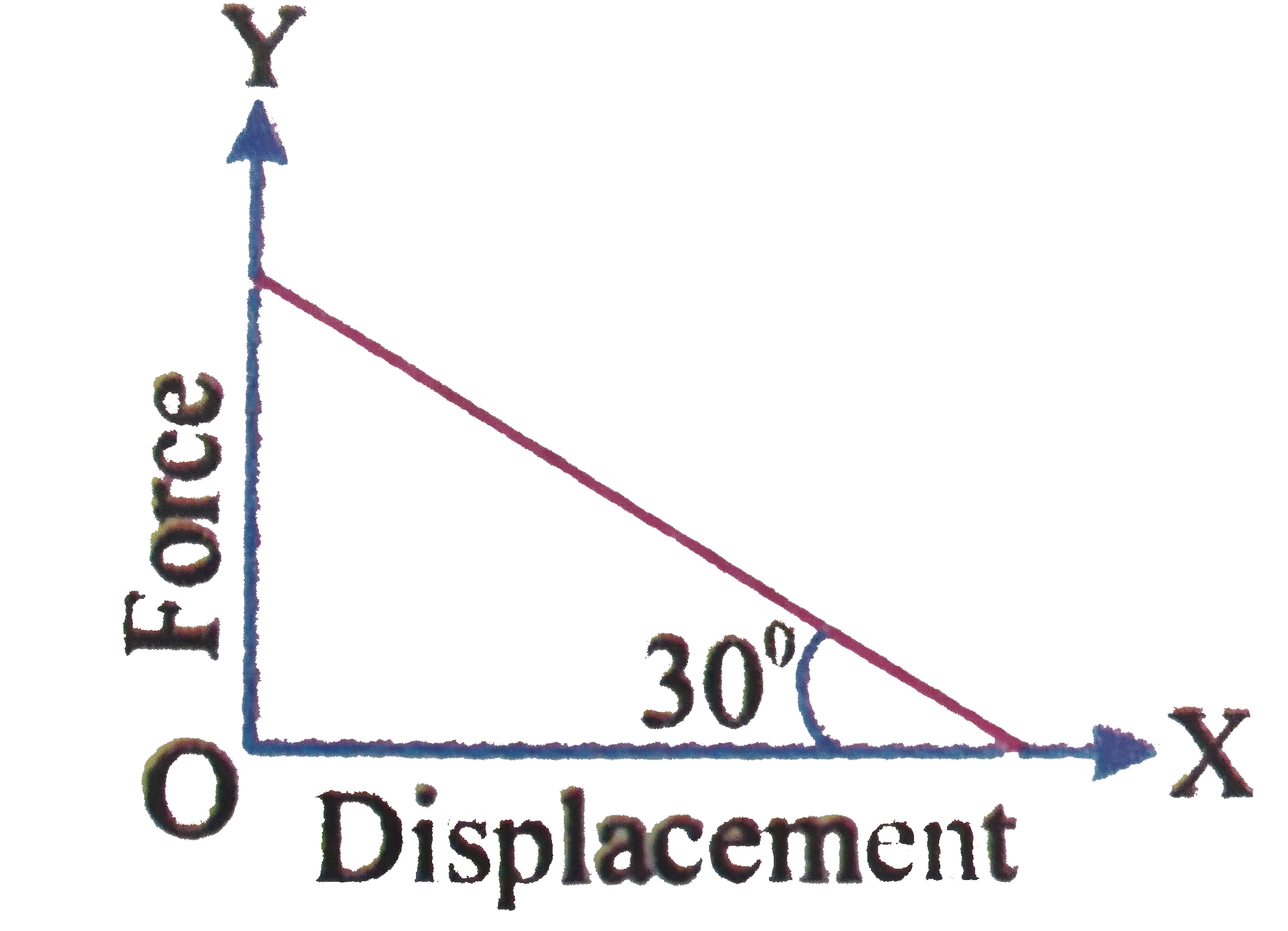
The value of force constant between the applied elastic force F and displacement will be
 A√3B1√3C12D√32
A√3B1√3C12D√32A mass M is suspended as shown in fig. The system is in equilibrium. Assume pulleys to be massless. K is the force constant of the spring.
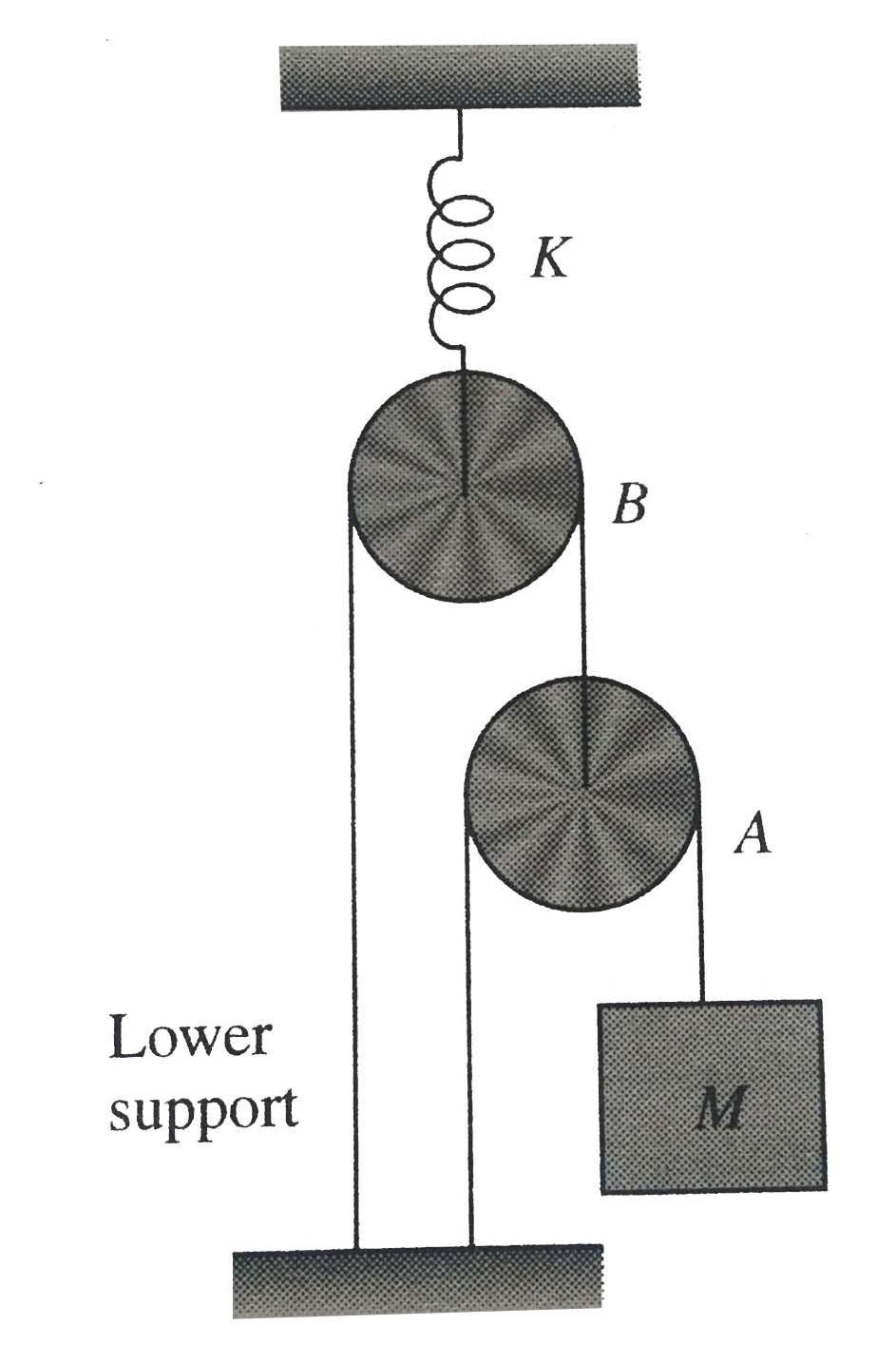
The extension produced in the spring is given byA4Mg/KBMg/KC2Mg/KD3Mg/KA mass M is suspended as shown in fig. The system is in equilibrium. Assume pulleys to be massless. K is the force constant of the spring.
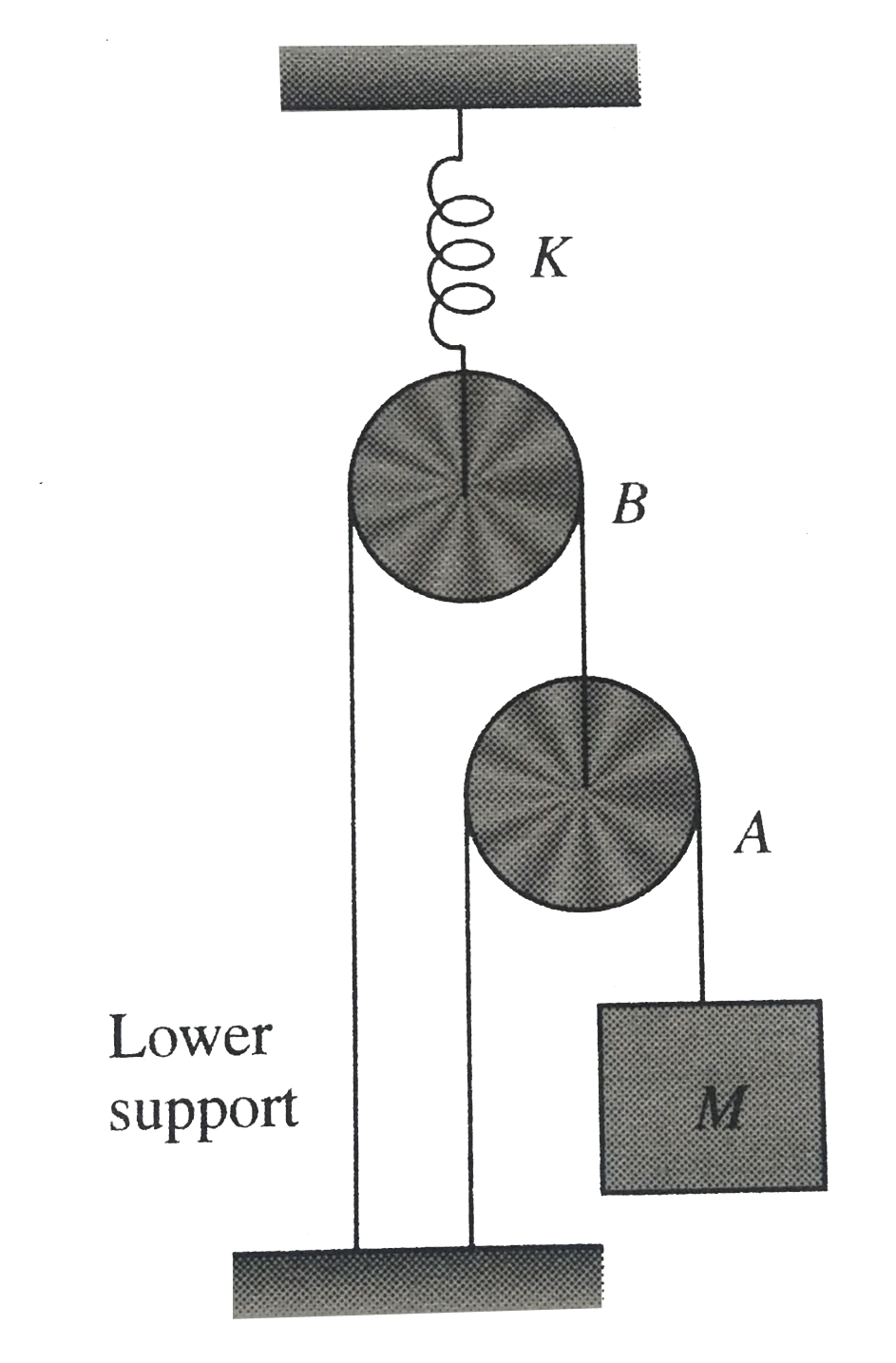
Find the net tension force acting on the lower support.AMgB2MgC3MgD4Mg
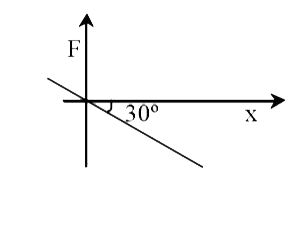
The force constant between the restoring force F and displacement x of a spring accoring to the graph shown will be
View SolutionA mass 1 kg is attaced to the hook of a spring and the spring is suspended vertically from a ceiling (see Fig. 5.12a). The spring is displaced from its equilibrium position by a distance x. The spring constant of the spring is 2.0×102 N/m. Calculate the displacement x.
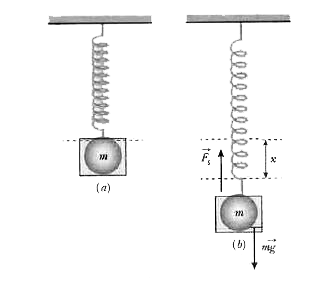
Figure 5-12 (a) Mass of 1 kg attached to a spring is suspended vertically. (b) Spring displace from equilibrium position by a distance x.
View SolutionFigure shows a system consisting of a massles pulley, a spring of force constant k and a block of mass m. If the block is sligthtly displaced vertically down from its equilibrium and released, find the period of its vertical oscillation in cases (a) and (b).

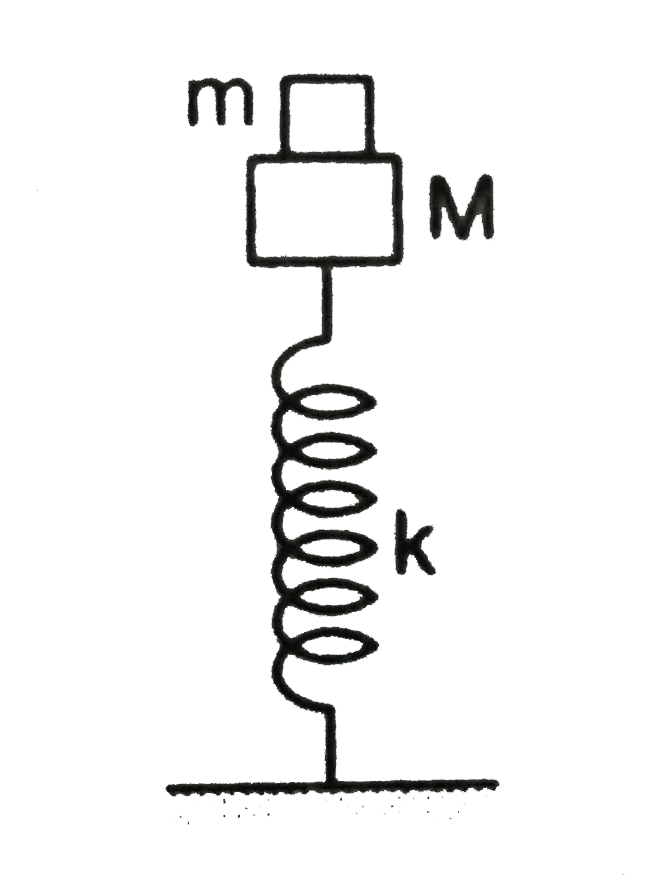
View SolutionA small block of mass m is kept on a bigger block of mass M which is attached to a vertical spring of spring constant k as shown in the figure. The system oscilates verticaly. a.Find the resultant force on the smaller block when it is displaced through a distance x above its equilibrium position. b. find the normal force on the smaller blok at this position. When is this force smallest smaller block at this position. When is this force smallest in magnitude? c. What can be the maximum amplitude with which the two blocks may oscillate together?
View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is

View Solution

