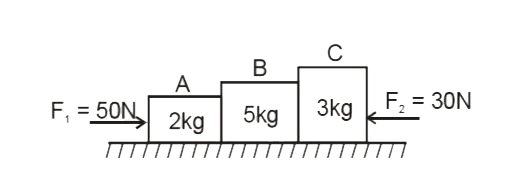
Write equations of forces in terms of the relative acceleration for the blocks shown in and find the relation between m and M so that system remains at rest
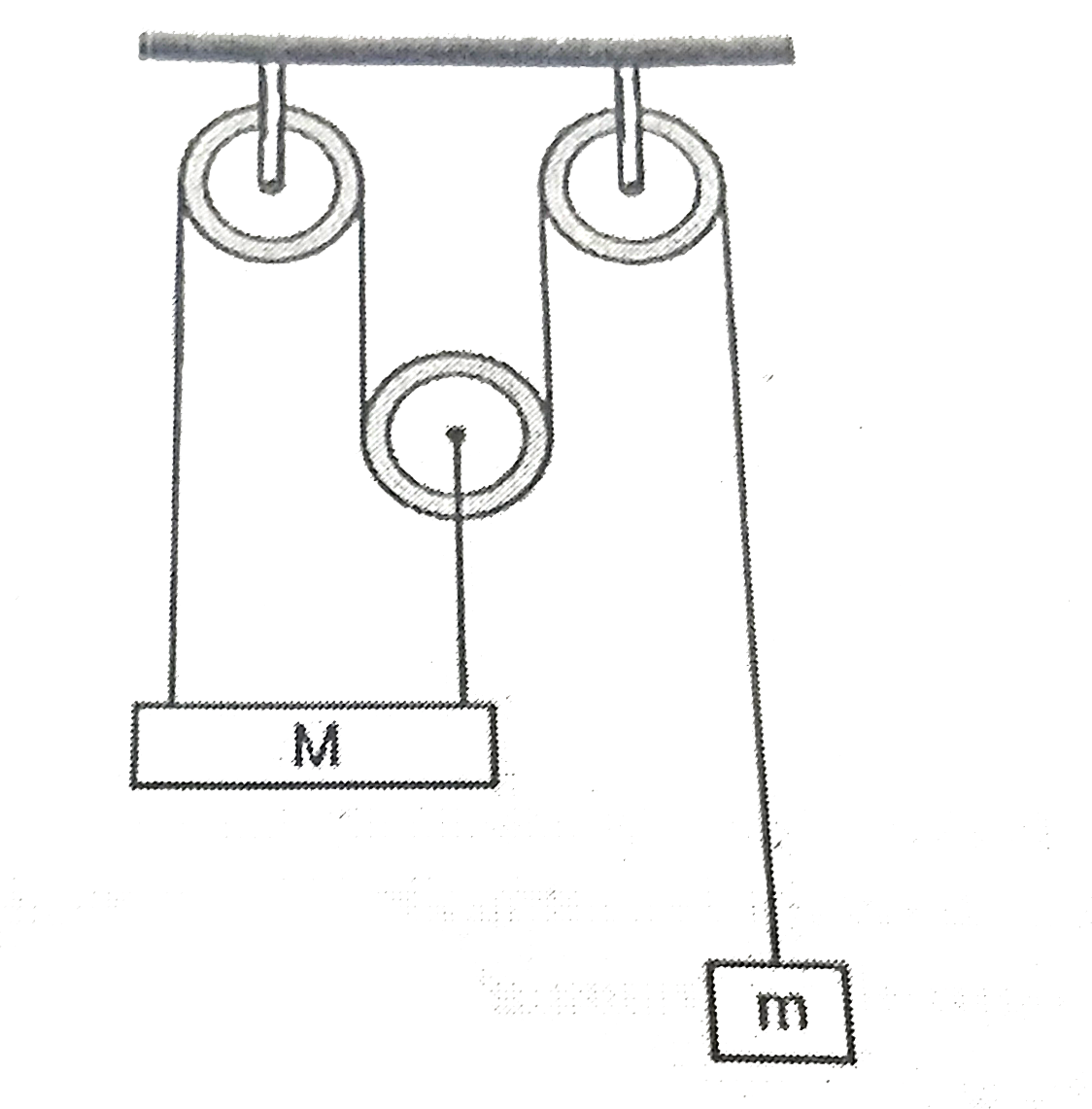
Total length of the cord
y1+3y2+l0=l
here y1 and y2 changes l0 and l remain constant
Differetiating Eq. (i) with respect to time, we get
dy1dt+3dy2dt=0
or v1+3v2=0 ....(ii)
also a1+3a2=0
which gives a1=3a2 (magnitude)
if we take a2=a up
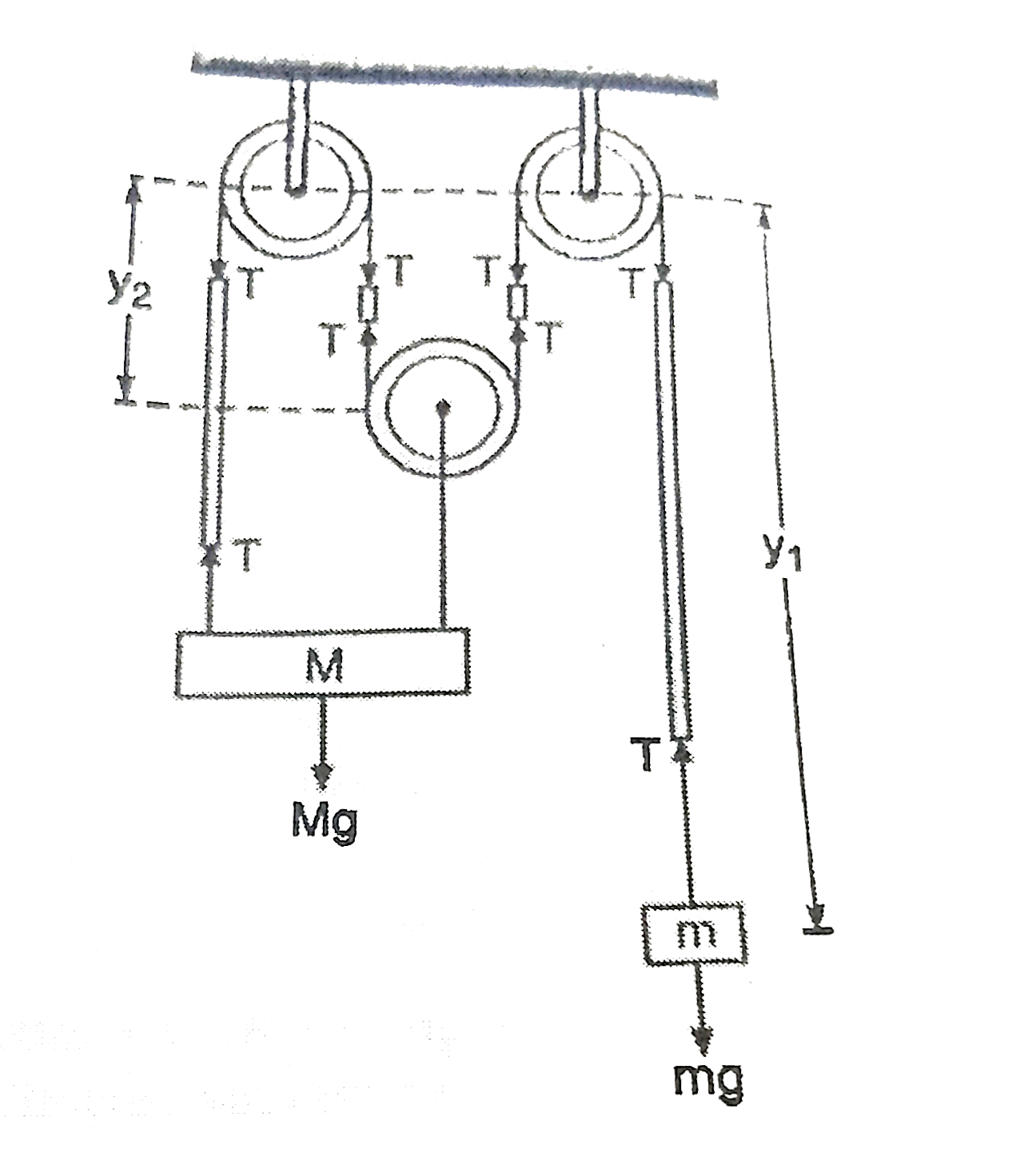
then a1=3a down
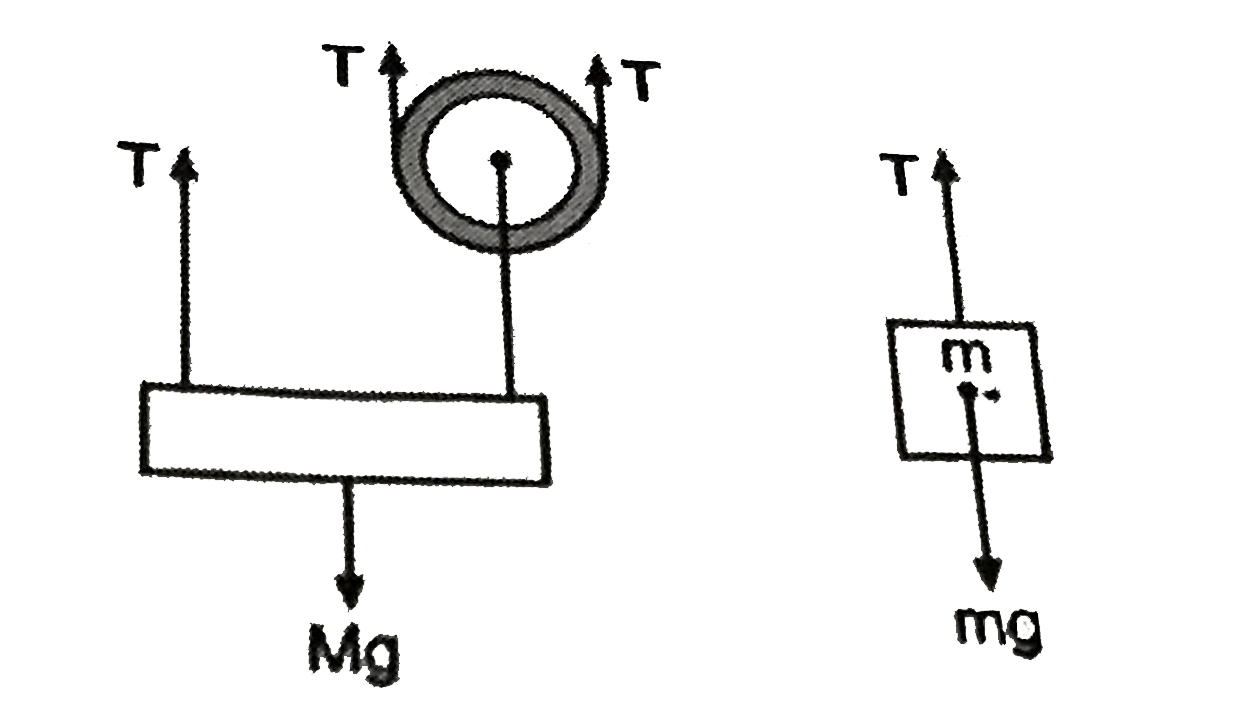
By Newton's second law we have
mg−T=m(3a)...(iii)
and 3T−Mg=Ma ....(iv)
Solving Eqs (iii) and (iv)
a=(3m−M)(9m+M)g
if system remains at rest a=0
∴3m=M
Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Problem for practice
Explore 30 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Objective Questions
Explore 134 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Comprehension
Explore 12 Videos
- BASIC MATHEMATICSBook:GRB PUBLICATIONChapter:BASIC MATHEMATICSExercise:Problems For Practice
Explore 35 Videos
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Comprehension type
Explore 11 Videos
Similar Questions
Knowledge Check
If system is in equilibrium then find relation between m1 and m2
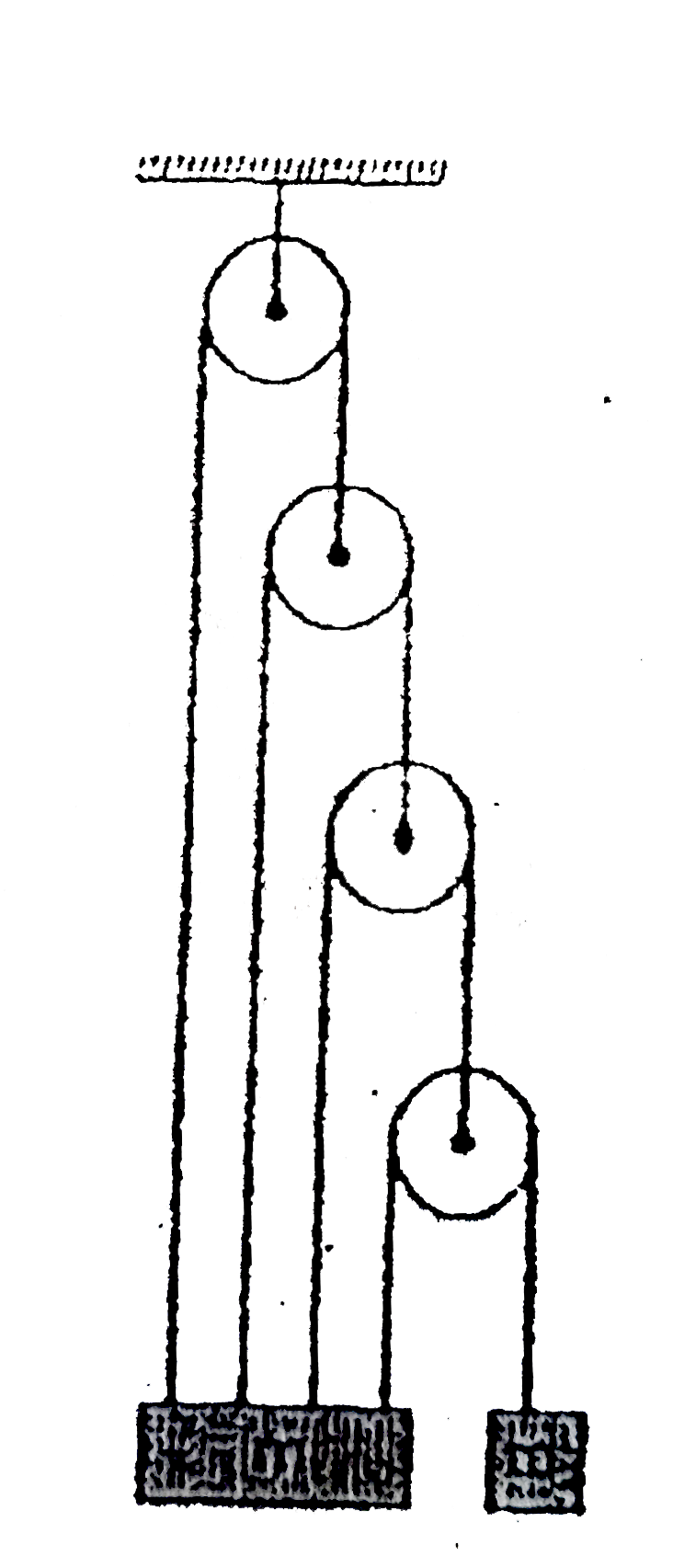 Am1m2=12Bm1m2=115Cm1m2=110Dm1m2=1
Am1m2=12Bm1m2=115Cm1m2=110Dm1m2=1A block of mass m is placed on a smooth inclined wedge ABC of inclination θ as shown in the figure. The wedge is given an acceleration 'a' towards the right. The relation between a and for the block to remain stationary on the wedge is:
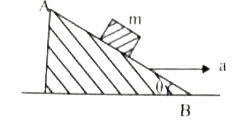 Aa=gcosθBa=gsinθCa=gcosecθDa=gtanθ
Aa=gcosθBa=gsinθCa=gcosecθDa=gtanθA block of mass m is placed on a smooth inclined wedge ABC of inclination theta as shown in the figure. The wedge is given an acceleration a towards the right. The relation between a and theta for the block to remain stationary on the wedge is.
 Aa=gtanθBa=gcosecθCa=cosθDa=gsinθ
Aa=gtanθBa=gcosecθCa=cosθDa=gsinθ
Two blocks of equal mass, M each, are connected to two ends of a massless string passing over a massless pulley. On one side of the string there is a bead of mass M2 .
(a) When the system is released from rest the bead continues to remain at rest while the two blocks accelerate. Find the acceleration of the blocks.
(b) Find the acceleration of the two blocks if it was observed that the bead was sliding down with a constant velocity relative to the string.
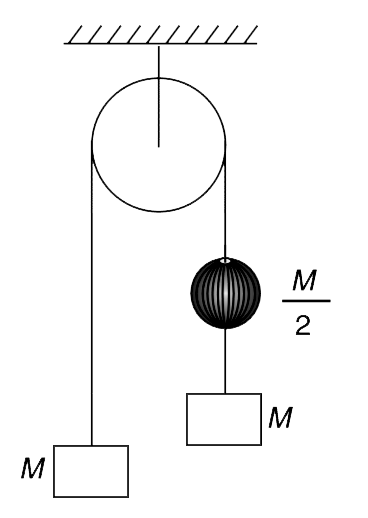
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m . A force P is applied to the other end of the rope . (a) Find the acceleration of the block and the rope . (b) Find the force that the rope exerts on the block M in terms of P, M and m .
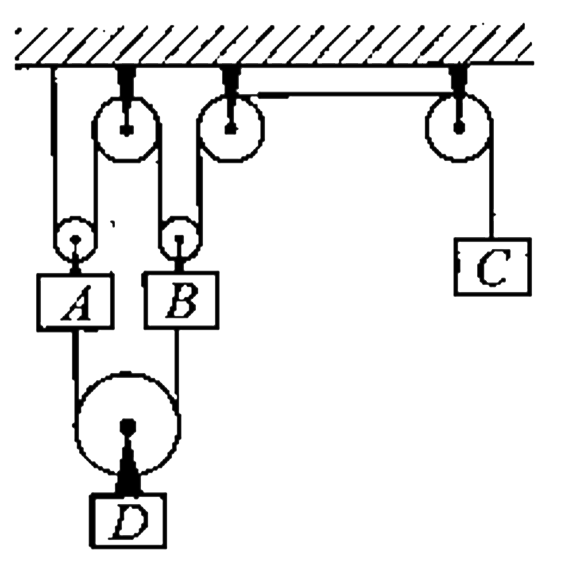
View SolutionThe system shown in figure starts from rest, and each block moves with a constant acceleration. If the relative acceleration of block C with respect to block B is 6m/s2 upward and the relative acceleration of block D with respect to block C after 3s from starts.
View SolutionIn terms of masses m1,m2 and g, find the acceleration of both the blocks shown in Fig. Neglect all friction and masses of the pulley.
View SolutionTwo blocks (mandM) are arranged as in figure Then is friction between ground and M only and other surface are frictionless between ground and Misμ=0.25 The maximum ratio of m and M(m/M) so that the system remain is at rest

View Solution