At wood machine is attached below the left hand pan of a physical balance while equal weight (M+m) g is placed in the right hand pan. The beam is horizontal when the masses M and m on the left hand side are braked What will happen if the masses M and m are unbraked on the left hand side?
Initially the system is in equilibium, so
FL=FR=(m+M)g ....(i)
When the L.H.S is unbraked, mass M will move downward while m upwards with acceleration
a=(M−m)M+mg
So, the tension in the string,
T=m(g+a)[orM(g−a)]=2mMg(M+m)
This in turn implies that force on L.H.S when the masses are in motion will be
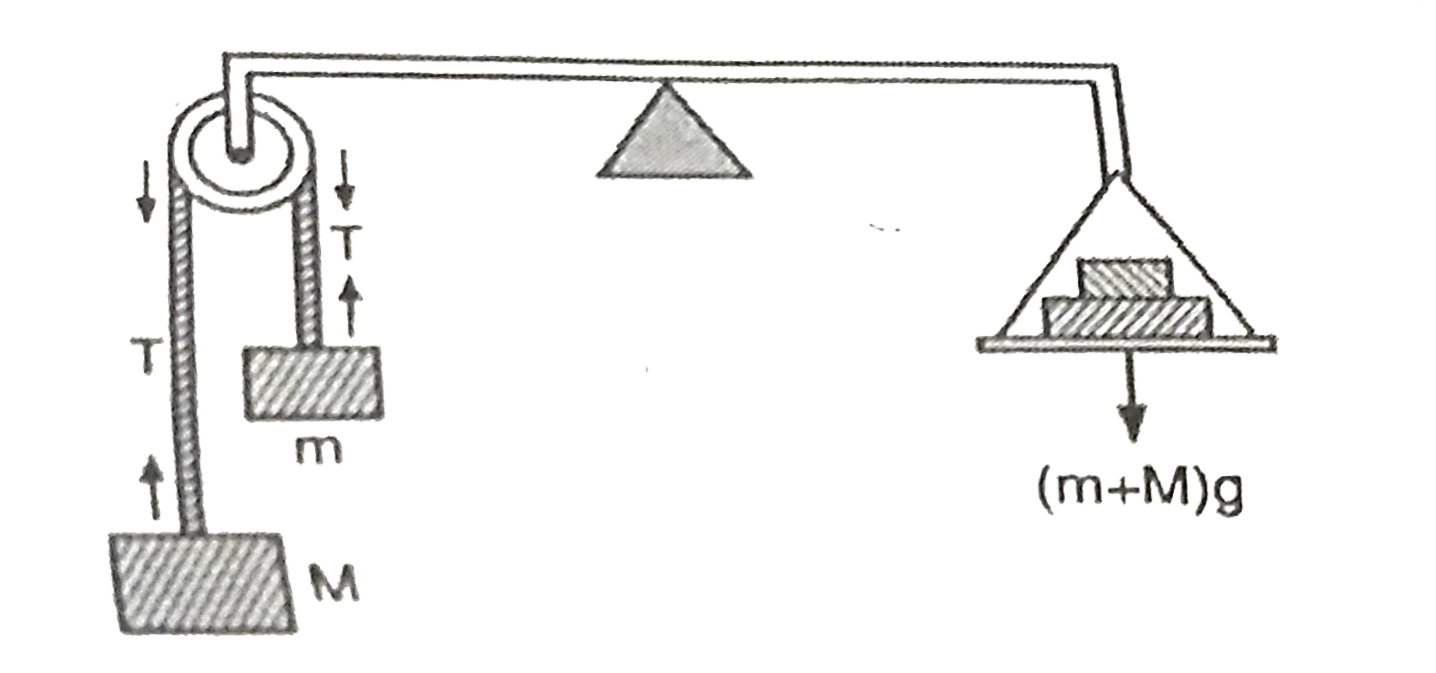
Now from Eqns (i) and (ii) it is clear that
FL−FL=(m+M)g−4mMg(M+m)
i.e., FL−FL=(M−m)2(M+m)g>0
i.e., FL>FLorFL<FL
i.e., the force on the left side decreases when the masses are unbraked and hence L.H.S will move up while R.H.S. down
Note: Physical reasoning When the masses of L.H.S are unbraked, M will move down while m up with same the weight of M will decrease (as accelerated down) while of m will increase (as accelerated up) As M>m decrease in weight will be more than increase So net weight on L.H.S will decrease and hence, it will move up.
Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Problem for practice
Explore 30 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Objective Questions
Explore 134 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Comprehension
Explore 12 Videos
- BASIC MATHEMATICSBook:GRB PUBLICATIONChapter:BASIC MATHEMATICSExercise:Problems For Practice
Explore 35 Videos
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Comprehension type
Explore 11 Videos
Similar Questions
What will be the acute angle between the hour-hand and the minute-hand at 2:13 p.m?
View SolutionTwo metal blocks A and B were placed on the two pans ofa common balance and the beam of the balance was horizontal. However, when the blocks were interchanged and block B was placed in the left pan and block A in the right pan, the beam was not balanced and tilted down toward the left. Discuss the various factors that could be the cause of this. Are the masses of two blocks equal?

View Solution
Knowledge Check
In a physical balance working on the principle of moments, when 5 mg weight is placed on the left pan, the beam becomes horizontal. Both the empty pans of the balance are of equal mass. Which of the following statements is correct ?
AEvery object that is weighted using this balance appears lighter than its actual weightBLeft arm is shorter than the right armCBoth the arms are of same lengthDLeft arm is longer than the right armA balance is made of a rigid rod free to rotate about a point not at the centre of the rod. When an unknown mass m is placed in the left pan, it is balanced by a mass m1 placed in the right pan and similarly when the mass m is placed in the right pan, it is balanced by a mass m2 in the left pan. Neglecting the masses of the pans, m is
Am1+m22B√m1m2C√m21+m222D√(m21+m22)2What will be the acute angle between the hour hand and the minute hand at 6:25 p.m.?
A30∘B40.5∘C42.5∘D35.5∘
A horizontal insulated cylinder is provided with frictionless non-conducting piston. On each side of the piston there is 50 litres of air at a pressure of 1 atmosphere and 273 K. Heat is slowly supplied to the air at the left hand side, until the piston has compressed the air on the right hand side to 2.5 atmosphere. Find Final temperature of air on the left hand side
View SolutionTwo metal blocks A and B were placed on the two pans ofa common balance and the beam of the balancec was horizontal. However, when the blocks were interchanged and block B was placed in the left pan and block A in the right pan, the beam was not balanced and tilted down toward the left. Discuss teh various factors that could be the cause of this. Are teh masses of two blocks equl?

View SolutionWhat would be the smaller of the two angles formed by the hour hand and the minute hand at 3:47 p.m.
View SolutionWhat would be the smaller of the two angles formed by the hour hand and the minute hand at 4 : 52 p.m.?
View SolutionA rigid massless beam is balanced by a particle of mass 4m in left hand side and a pulley particle system in right hand side. The value of xy is
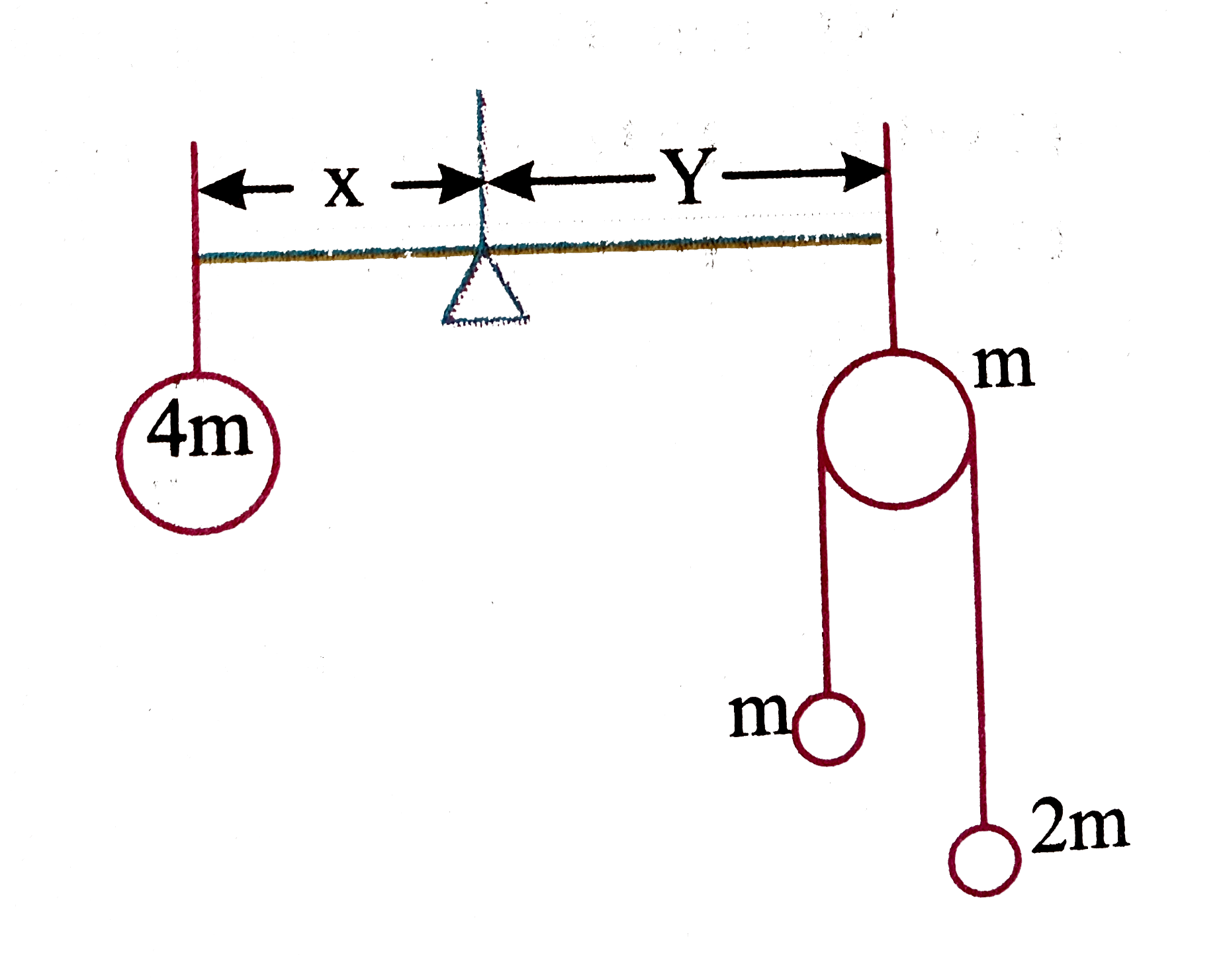
View Solution

