Find the time period of mass M when displaced from its equilibrium position and then reelased for the system shown in figure.
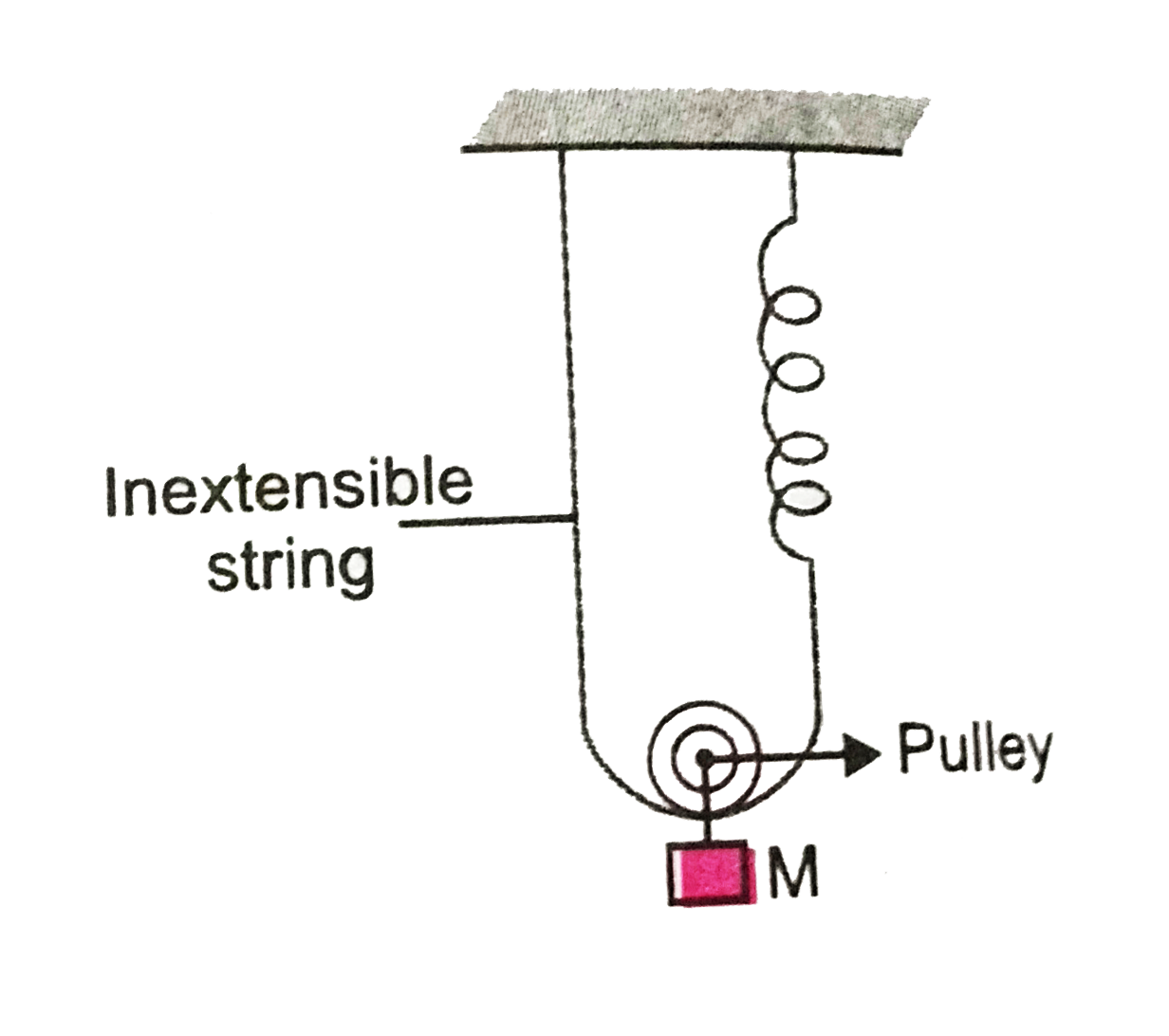
Let k be the spring constant of the spring. When mass M is suspended from the given system as shown in figure.let l be the length through which mass M moves down before it comes to rest. In this situation, both the spring and string will be stretched by length l. Since string is inextensible, so spring is stretched by length 2l. The tension along the string is the same. So, restoring force is
F=−2k×(2l)=−4kl ...(i)
In equilibrium position,this restoring balances weigth of the mass. i.e.,
Mg=4kl
If mass M is pulled doen through small distance y, then restoring force F′ is given by
F′=−2k(2l+2y)
Effective restoring force on mass M is given by
f=F′−F=−2(2l+2y)−(−4kl)=−4ky ...(iii)
As f∝y and f is directed towards equilibrium position. hence if mass is left free, it will execute linear SHM. From (ii), spring factor=4k.
Inertia factor =M
As time period, T=2π√inertiafactorspringfactor=2π√M4k
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Long Answer Questions
33 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Advanced Problems For Competitions
20 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Very Short Answer Questions
99 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
Similar Questions
Knowledge Check
A small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
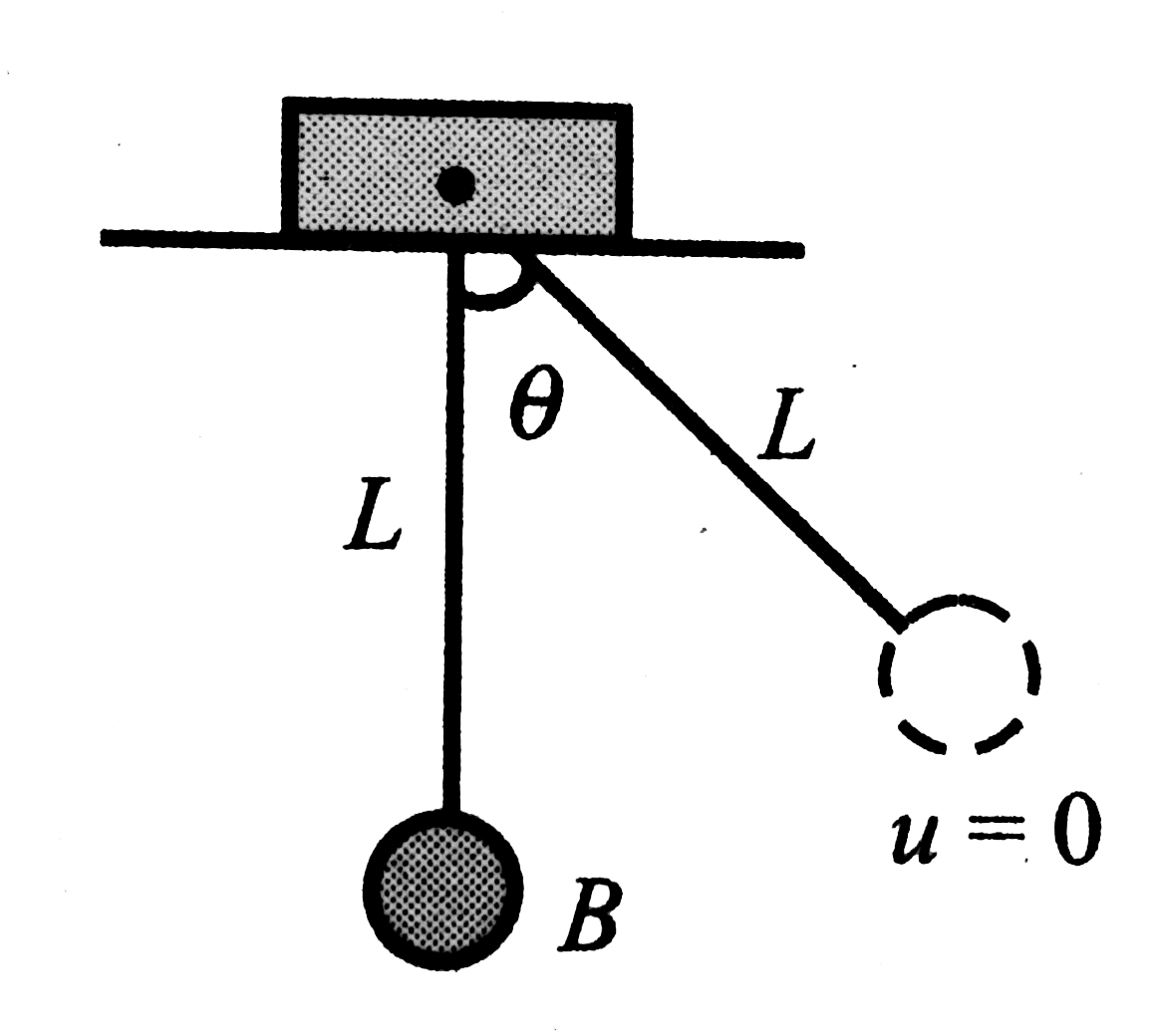 The displacement of centre of mass of A+B system till the string becomes vertical is AzeroBL(1−cosθ)CL2(1−cosθ)Dnone of these
The displacement of centre of mass of A+B system till the string becomes vertical is AzeroBL(1−cosθ)CL2(1−cosθ)Dnone of theseA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
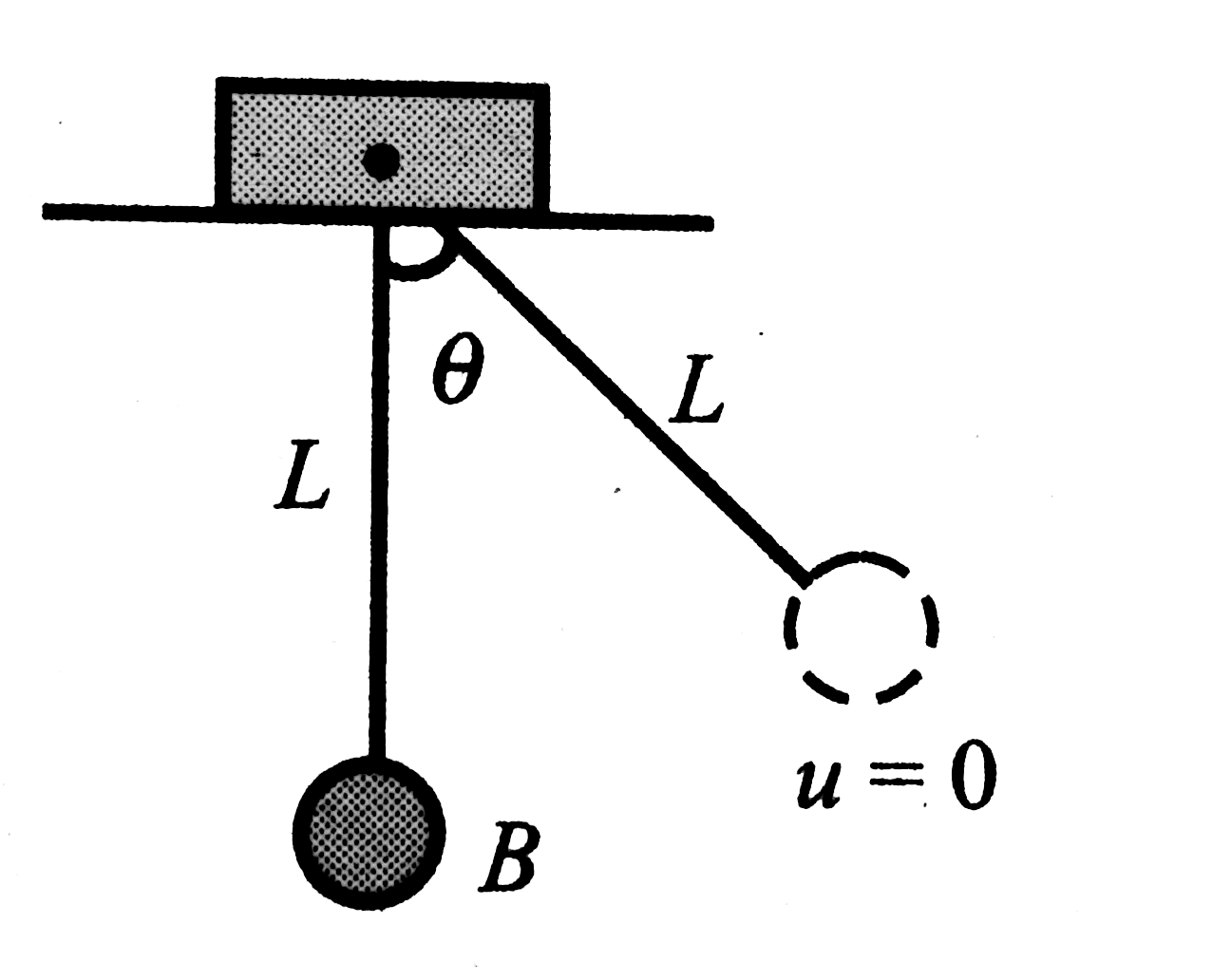
Tension in string when it is vertical, isAmgBmg(2−cosθ)Cmg(3−2cosθ)Dnone of theseFigure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
 A2π√mKBπ√m4KCπ√mKD4π√mK
A2π√mKBπ√m4KCπ√mKD4π√mK
A particle of mass m is suspended from a fixed point O by a string length l.At t=0, it is displaced from its equilibrium position and released.If T is the tension in the string with time t, then the correct graph is
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximu speed of the trolley is
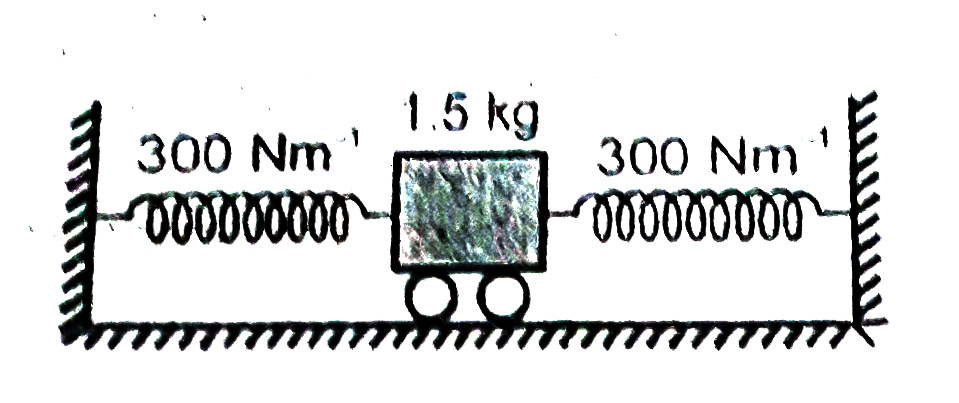
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shwon in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find th eperiod of oscillation.

View SolutionA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.

The displacement of block when equilibrium position is
View Solution


