Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

For the calculation purpse, in this situation we will neglect gravity because it is constant throughout and will not effect the net restoring force.
Let in the equilibrium position, the spring has extended by an amount x0
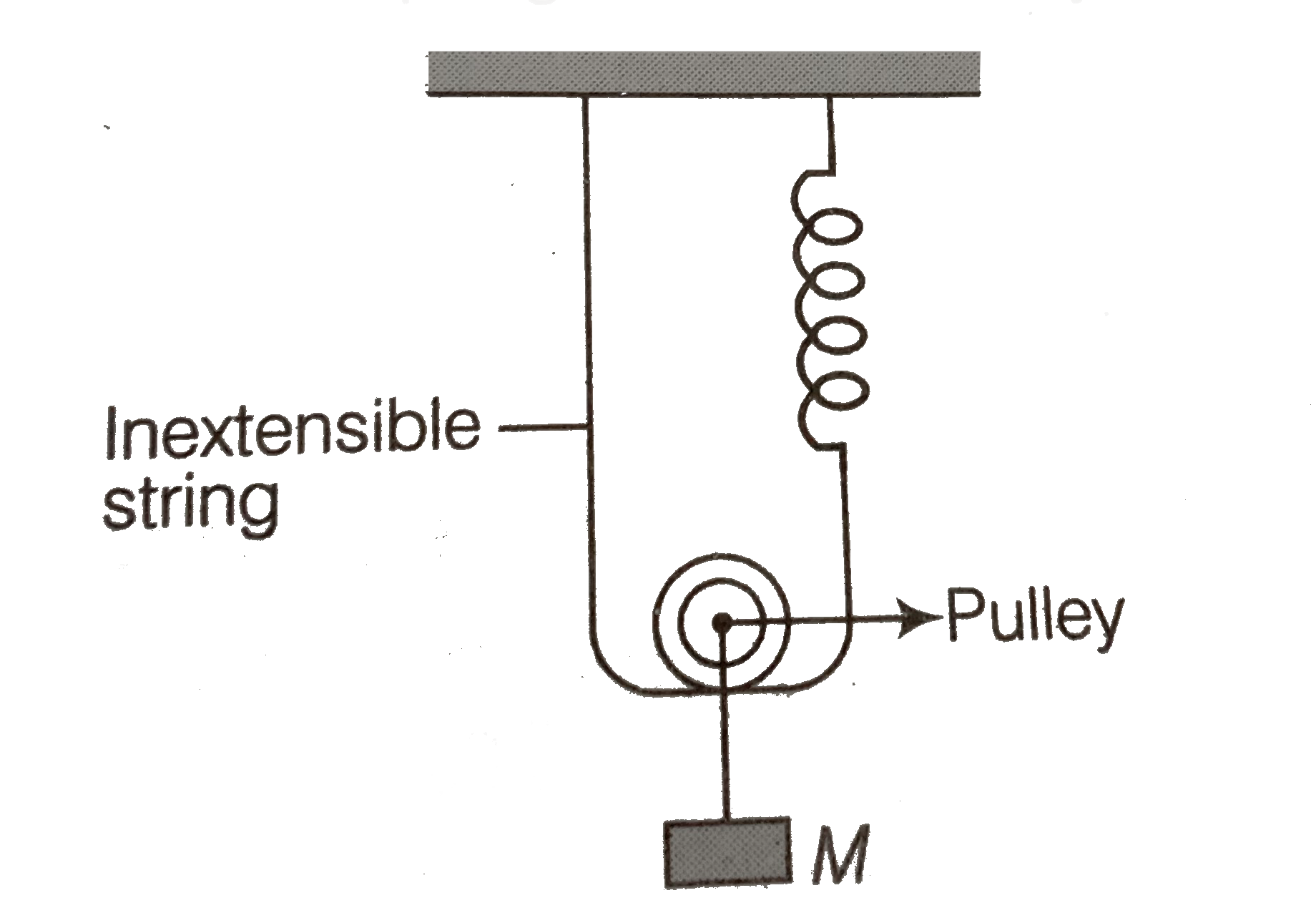
Now, if the mass is given a further displacement downwards by an amount x. The string and spring both should increase in length by x.
But, string is inextensible, hence the spring alone will contribute the total extension x+x=2x, to lower the mass down by x from initial equilibrium mean position x0. So, net extension in the spring (=2x+x0).
 Now force on the mass before bulling (in the xoextension caes)
Now force on the mass before bulling (in the xoextension caes)
F=2T
But T=kx0 [where k is spring constant]
∴F=2kx0 ....(i)
When the mass is lowered down further by x,
F'=2T['
But new spring length =(2x+x0)
∴F'=2k(2x+x0) .....(ii)
Restoring force on the system.
Frestoring=−[F'−F]

Using Eqs. (i) and (ii), we get
Frestoring=−[2k(2x+x0)−2kx0]
=−[2×2kx+2kx0−2kx0]
=−4kx
or Ma=−4kx
where, a= acceleration " " (As, F =ma)
⇒a=−(4kM)x
k1 M being constant.
∴a∝−x
Hence, motion is SHM.
Comparing the above accleration expression with standard SHM equation a=−ω2x, we get
ω2=4kM⇒ω=√4kM
:. Time period T=2πω=2π√4kM=2π√M4k
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE Book:NCERT EXEMPLAR ENGLISHChapter:MOTION IN A STRAIGHT LINE Exercise:Very Short Answer Type Qns
Explore 14 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NCERT EXEMPLAR ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:Long answer type questions
Explore 12 Videos
Similar Questions
Find the period of oscillation of the system shown in figure.

View SolutionA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
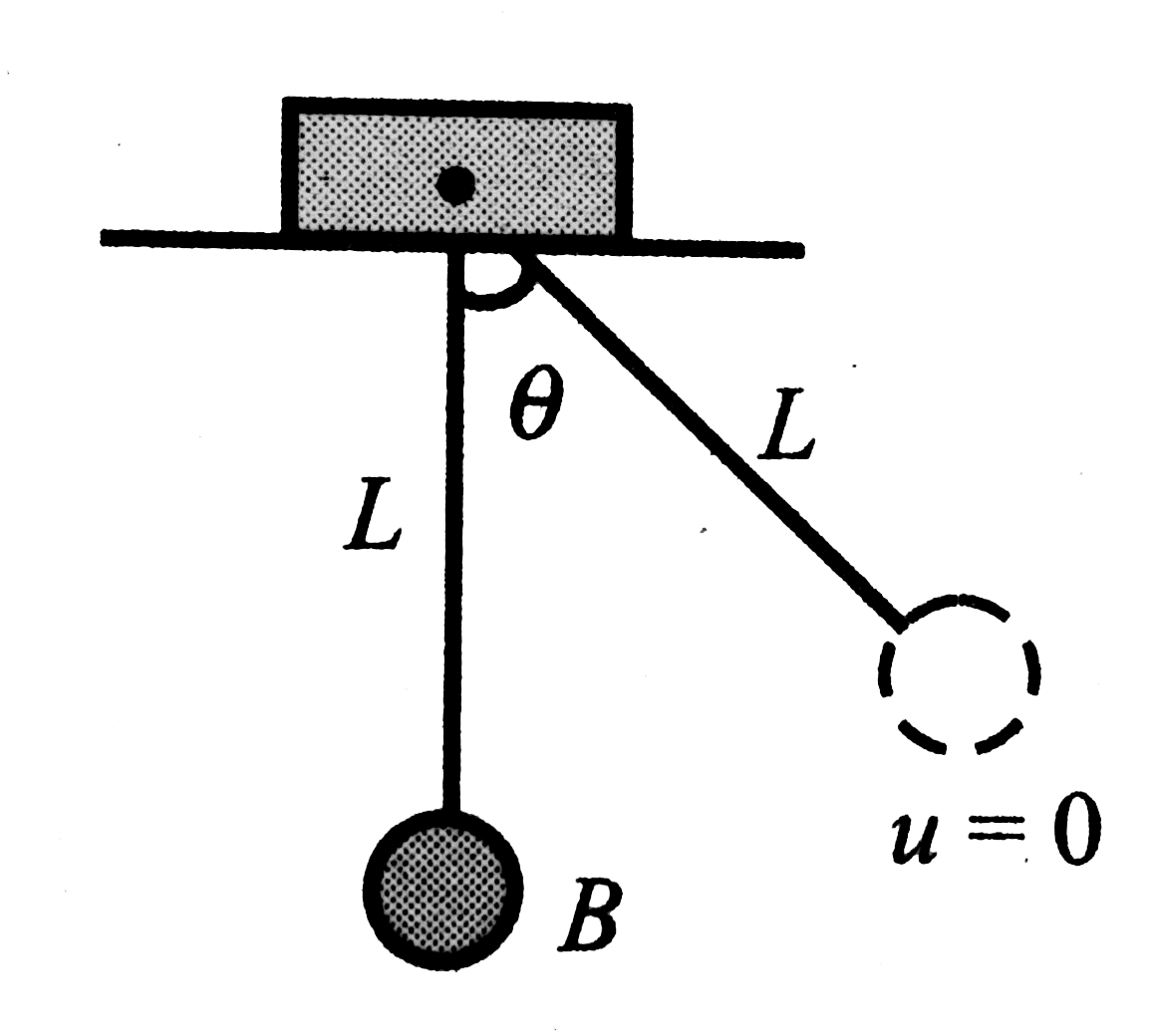 The displacement of centre of mass of A+B system till the string becomes vertical is
The displacement of centre of mass of A+B system till the string becomes vertical is
View SolutionA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
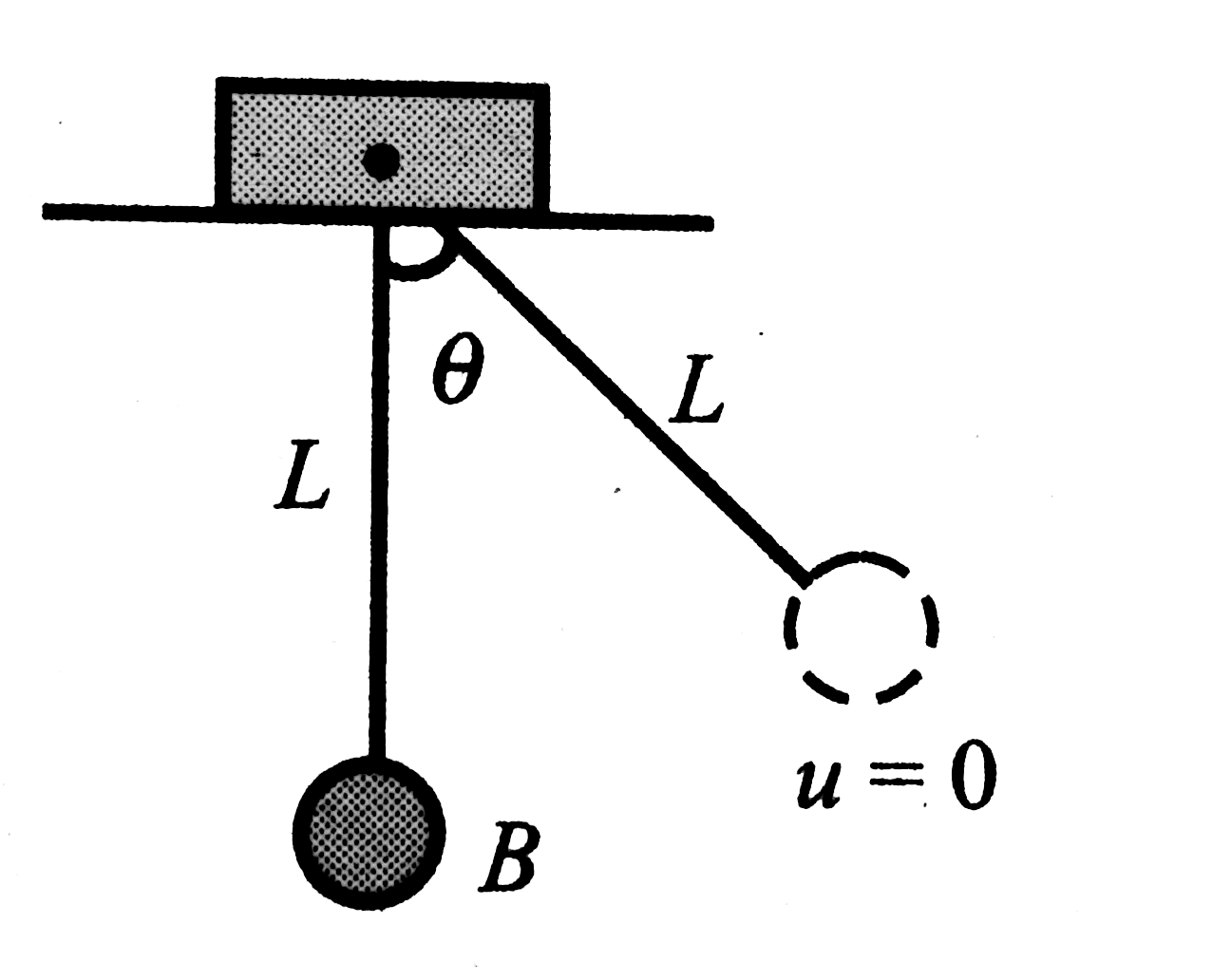
Tension in string when it is vertical, is
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximum speed of the trolley is
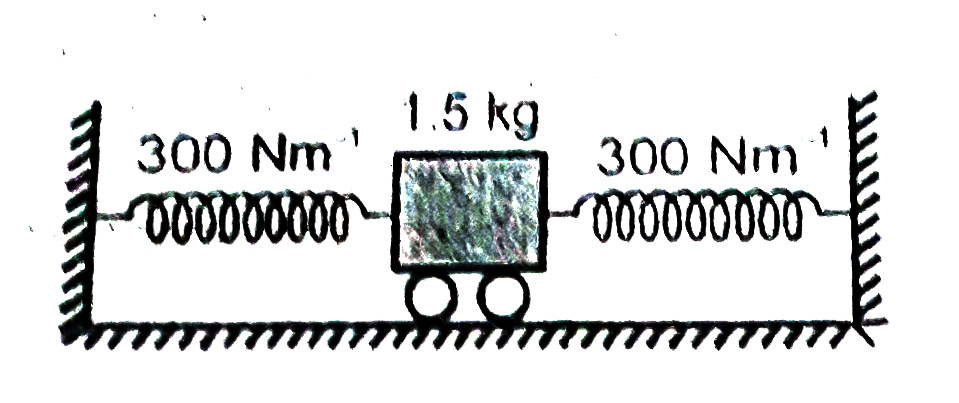
View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is

View SolutionA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.

The displacement of block when equilibrium position is
View SolutionFigure-1 to Figure -4 shows four different spring arrangements . Mass m in each arrangement is displacement from its equilibrium position and released Neglec mass of the springs. Choose the correct statement (s)

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillation.

View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

View SolutionA mass of 0.5 kg is hung from a spring. A gradually increasing 0.5 N force is required to pull the mass downward a distance of 0.25 m from its equilibrium position,if the mass is then released from this position, find
(a) The total energy of the system .
(b) The frequency of the oscillation
(c ) The speed and acceleration of the mass as it passes the equilibrium position.
(d) The speed and acceleration of the mass when the diplacement from equilibrium is 0.25 m
(e) For the initial condition stated, write down the diplacement equation of motion for this mass.
View Solution

