A person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0s−1 and an amplitude 5.0 cm. A weighing machine on the platform gives the persons wieght against time.
(a) Will there be any change in weight of the body, during the oscillation?
(b) If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?
To solve the problem step by step, we will analyze the oscillation of the platform and how it affects the reading on the weighing machine.
Step 1: Understanding the Weight Change During Oscillation
The weight of a person on a weighing machine is the normal force exerted by the machine. When the platform oscillates, the acceleration of the platform changes, which affects the normal force and hence the reading on the weighing machine.
Hint: Consider how acceleration affects the normal force acting on the person.
Step 2: Determine the Acceleration of the Platform
The acceleration of the platform can be expressed in terms of the angular frequency (ω) and the amplitude (A) of the oscillation. The formula for acceleration (a) is given by:
a=−ω2A
Where:
- ω=2πf (f is the frequency)
- A is the amplitude of oscillation.
Given:
- Frequency f=2.0s−1
- Amplitude A=5.0cm=0.05m
Calculating ω:
ω=2π(2.0)=4πrad/s
Calculating acceleration:
a=−ω2A=−(4π)2(0.05)=−16π2(0.05)
Hint: Remember to convert the amplitude into meters before calculations.
Step 3: Calculate the Maximum and Minimum Readings on the Weighing Machine
The normal force (N) exerted by the weighing machine can be calculated using the following equations based on the direction of the oscillation:
1. When the platform is at the lowest position (maximum reading):
Nmax=mg+ma
Nmax=mg+m(−ω2A)
Nmax=mg+m(16π2(0.05))
2. When the platform is at the highest position (minimum reading):
Nmin=mg−ma
Nmin=mg−m(16π2(0.05))
Where m=50kg and g=9.8m/s2.
Calculating Nmax and Nmin:
- First, calculate mg:
mg=50×9.8=490N
- Now calculate ma:
ma=50×16π2(0.05)
ma=50×16×9.87×0.05
ma≈50×0.793≈39.65N
Now substituting these values:
1. Maximum Reading:
Nmax=490+39.65≈529.65N
2. Minimum Reading:
Nmin=490−39.65≈450.35N
Final Answers:
(a) Yes, there will be a change in the weight of the body during the oscillation.
(b) The maximum reading on the machine will be approximately 529.65N (at the lowest position of oscillation) and the minimum reading will be approximately 450.35N (at the highest position of oscillation).
The weight of a person on a weighing machine is the normal force exerted by the machine. When the platform oscillates, the acceleration of the platform changes, which affects the normal force and hence the reading on the weighing machine.
The acceleration of the platform can be expressed in terms of the angular frequency (ω) and the amplitude (A) of the oscillation. The formula for acceleration (a) is given by:
a=−ω2A
Where:
- ω=2πf (f is the frequency)
- A is the amplitude of oscillation.
- Frequency f=2.0s−1
- Amplitude A=5.0cm=0.05m
ω=2π(2.0)=4πrad/s
a=−ω2A=−(4π)2(0.05)=−16π2(0.05)
The normal force (N) exerted by the weighing machine can be calculated using the following equations based on the direction of the oscillation:
Nmax=mg+ma
Nmax=mg+m(−ω2A)
Nmax=mg+m(16π2(0.05))
Nmin=mg−ma
Nmin=mg−m(16π2(0.05))
- First, calculate mg:
mg=50×9.8=490N
ma=50×16π2(0.05)
ma=50×16×9.87×0.05
ma≈50×0.793≈39.65N
1. Maximum Reading:
Nmax=490+39.65≈529.65N
Nmin=490−39.65≈450.35N
(a) Yes, there will be a change in the weight of the body during the oscillation.
(b) The maximum reading on the machine will be approximately 529.65N (at the lowest position of oscillation) and the minimum reading will be approximately 450.35N (at the highest position of oscillation).
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE Book:NCERT EXEMPLAR ENGLISHChapter:MOTION IN A STRAIGHT LINE Exercise:Very Short Answer Type Qns
Explore 14 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NCERT EXEMPLAR ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:Long answer type questions
Explore 12 Videos
Similar Questions
A person normally weighing 60kg stands on a platform which oscillates up and down harmonically at a frequency 2.0sec−1 and an amplitude 5.0cm . If a machine on the platform gives the person's weight against time deduce the maximum and minimum reading it will shown, Takeg=10m/sec2.
View SolutionA man is standing on a platform moving up and down as a S.H.M. will there be any change in his weight as recorded by a weighing machine on the platform ?
View Solution
Knowledge Check
A simple harmonic oscillator has a frequency of 2.5 Hz and an amplitude of 0.05m. What is the period of the oscillations?
A0.4sB0.2sC8sD20s
Passage XIII) Mr. Anoop having mass 50 kg is standing on a massless platform which oscillates up and down (doing SHM) of frequency 0.5 sec−1 and amplitude 0.4m. Platforms has a weighing machine fitted in it (Which is also massless). On which Anoop is standing. (Take (π2) = 10 and g = 10 m/s2. Assume that at t=0 (Platform+Anoop) is at their highest point of oscillation. [More than one option is correct]
Which of the following will be correct for reading of weighting machine
View SolutionA person is holding a suitcase and moving on a horizontal platform. Is he doing any work?
View SolutionA man weighing 60kg stands on the horizontal platform of a spring balance. The platform starts executing simple harmonic motion of amplitude 0.1m and frequency 2π. its which of the following statement is correct ?

View SolutionA coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time
View SolutionA 0.5kg body performs simple harmonic motion with a frequency of 2Hz and an amplitude of 8mm. Find the maximum velocity of the body, its maximum acceleration and the maximum restoring force to which the body is subjected.
View SolutionA 80 kg man is standing on a weightless weighing machine as shown in the figure if mass of hanging block is 40 kg, then reading of weighing machine, is
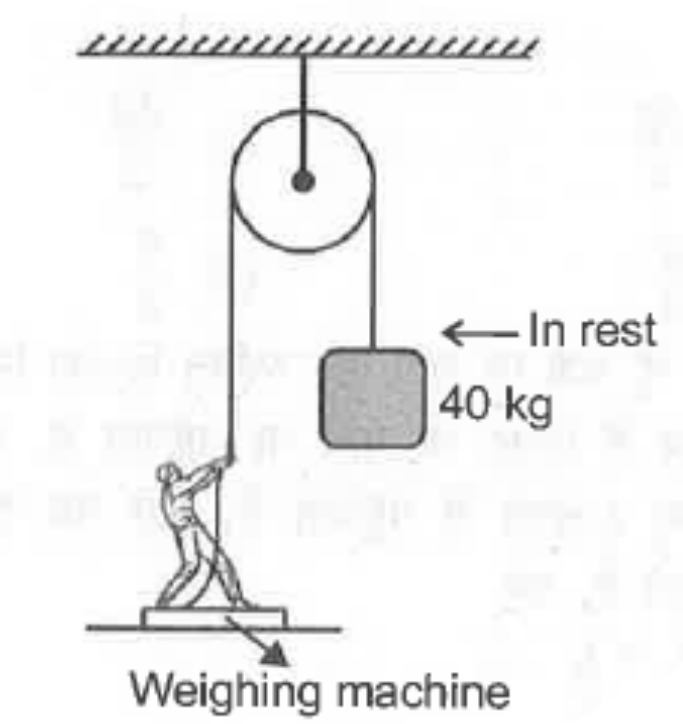
View SolutionA lift carries a person with a weighting machine in it, up and then down with the same constant acceleration. The weights recorded by the machine in the two cases are in the ratio 5:3. The acceleation of the lift is
View Solution