A body of mass m is attached ot one end of a massless spring which is suspended vertically form a fixed point. The mass is held in hand, so that the spring is neither stretched nor compressed. The lowest position attained by the mass during oscillation is 4 cm below the point, where it was held in hand.
(a) What is the amplitude of oscillation?
(b) Find the frequency of oscillation?
To solve the problem step by step, we will break it down into two parts: (a) finding the amplitude of oscillation and (b) finding the frequency of oscillation.
Part (a): Finding the Amplitude of Oscillation
1. Understanding the Setup:
- We have a mass m attached to a massless spring, which is suspended vertically.
- The mass is held in hand, meaning the spring is neither stretched nor compressed.
- When released, the mass moves downwards, and the lowest position attained is 4 cm below the initial position.
2. Identifying the Lowest Point:
- Let the lowest point reached by the mass during oscillation be denoted as x.
- Given that x=4 cm, this is the maximum displacement from the mean position.
3. Mean Position and Amplitude:
- The mean position is where the spring is at its natural length when the weight of the mass is balanced by the spring force.
- The amplitude A of oscillation is defined as the maximum displacement from the mean position.
- Since the lowest position is 4 cm below the initial position where the mass was held, the amplitude of oscillation is:
A=4 cm
Part (b): Finding the Frequency of Oscillation
1. Using the Formula for Frequency:
- The frequency f of oscillation can be calculated using the formula:
f=1T
- Where T is the time period of oscillation given by:
T=2π√mk
- Here, k is the spring constant.
2. Relating the Spring Constant to the Given Information:
- From the equilibrium position, we know that the force due to gravity on the mass is balanced by the spring force:
mg=kx′
- Where x′ is the extension of the spring at equilibrium. From the earlier analysis, we know:
x′=mgk
- The lowest point x can be expressed in terms of k and m:
x=2mgk
- Given that x=4 cm=0.04 m, we can rearrange this to find k/m:
k=2mgx
3. Substituting into the Frequency Formula:
- Substitute k into the frequency formula:
f=12π√km=12π√2gx
- Plugging in g=9.8 m/s2 and x=0.04 m:
f=12π√2×9.80.04
- Calculate the value:
f=12π√19.60.04=12π√490≈16.2832×22.14≈3.52 Hz
Final Answers:
- (a) The amplitude of oscillation is 4 cm.
- (b) The frequency of oscillation is approximately 3.52 Hz.
- We have a mass m attached to a massless spring, which is suspended vertically.
- The mass is held in hand, meaning the spring is neither stretched nor compressed.
- When released, the mass moves downwards, and the lowest position attained is 4 cm below the initial position.
- Let the lowest point reached by the mass during oscillation be denoted as x.
- Given that x=4 cm, this is the maximum displacement from the mean position.
- The mean position is where the spring is at its natural length when the weight of the mass is balanced by the spring force.
- The amplitude A of oscillation is defined as the maximum displacement from the mean position.
- Since the lowest position is 4 cm below the initial position where the mass was held, the amplitude of oscillation is:
A=4 cm
- The frequency f of oscillation can be calculated using the formula:
f=1T
- Where T is the time period of oscillation given by:
T=2π√mk
- Here, k is the spring constant.
- From the equilibrium position, we know that the force due to gravity on the mass is balanced by the spring force:
mg=kx′
- Where x′ is the extension of the spring at equilibrium. From the earlier analysis, we know:
x′=mgk
- The lowest point x can be expressed in terms of k and m:
x=2mgk
- Given that x=4 cm=0.04 m, we can rearrange this to find k/m:
k=2mgx
- Substitute k into the frequency formula:
f=12π√km=12π√2gx
- Plugging in g=9.8 m/s2 and x=0.04 m:
f=12π√2×9.80.04
- Calculate the value:
f=12π√19.60.04=12π√490≈16.2832×22.14≈3.52 Hz
- (a) The amplitude of oscillation is 4 cm.
- (b) The frequency of oscillation is approximately 3.52 Hz.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE Book:NCERT EXEMPLAR ENGLISHChapter:MOTION IN A STRAIGHT LINE Exercise:Very Short Answer Type Qns
Explore 14 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NCERT EXEMPLAR ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:Long answer type questions
Explore 12 Videos
Similar Questions
"A mass is attached to one end of a spring and by holding the other end in hand, the spring is whirled in a horizontal circle" What happens to the length of the spring ?
View SolutionA mass M=5 kg is attached to a string as shown in the figure and held in position so that the spring remains unstretched. The spring constant is 200Nm−1 . The mass M is then released and begins to undergo small oscillations. The amplitude of oscillation is
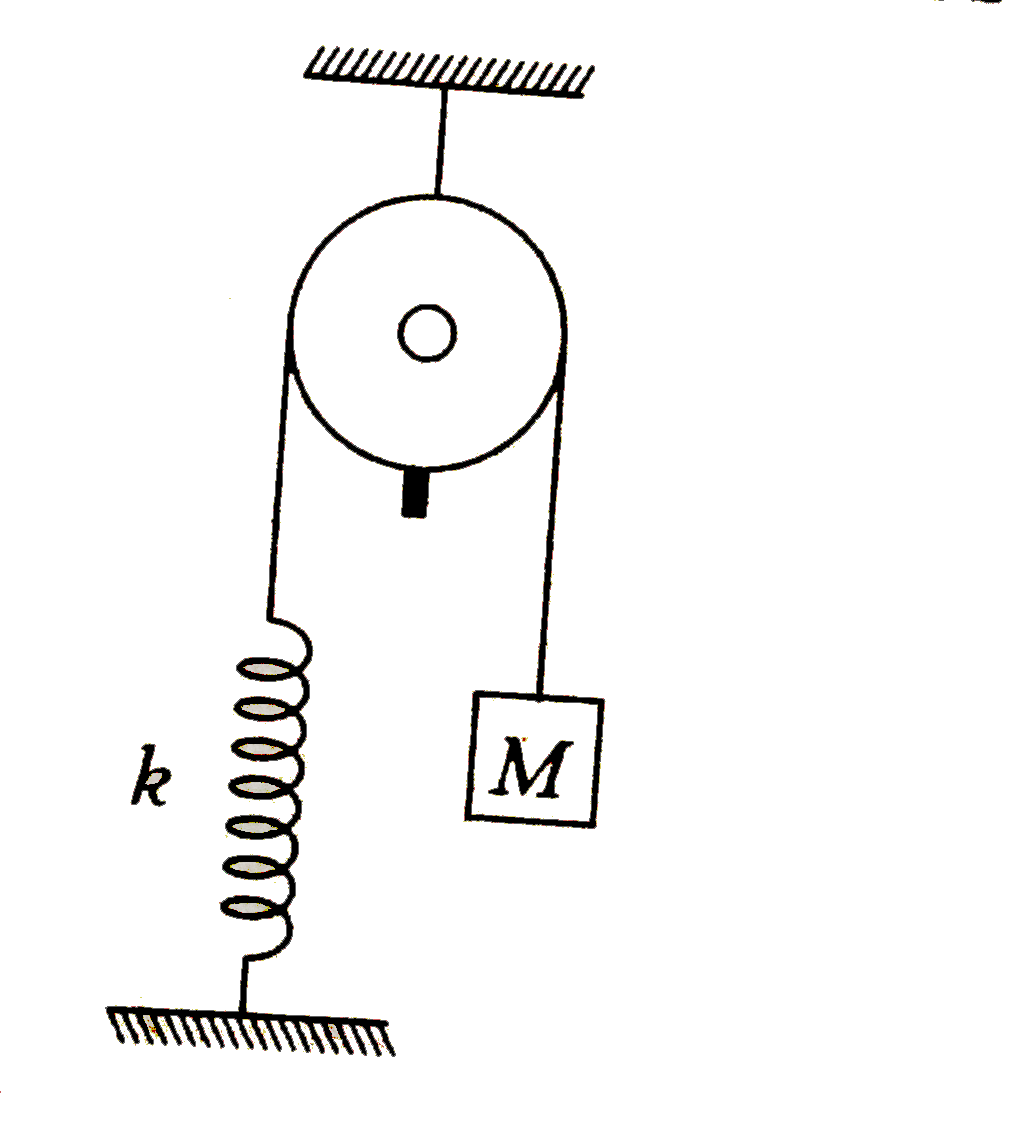
View Solution
Knowledge Check
A body of mass m is attached to one end of a massless spring which is suspended vertically from a fixed point. The mass is held in hand so that the spring is neither stretched nor compressed. Suddenly the support of the hand is removed. The lowest position attained by the mass during oscillation is 4cm below the point, where it was held in hand.
(a) What is the amplitude of oscillation ?
(b) Find the frequency of oscillation?A1 cm, 4.5HzB2 cm, 3.51HzC3 cm, 2.51HzD4 cm, 1.5Hz
If the mass attached to a vertical spring is pulled down and left, it oscillates. why ?
View SolutionA body of mass m attached to a spring which is oscillating with time period 4 s. If the mass of the body is increased by 4 kg, its time period increases by 2 s. Determine value of initial mass m.
View SolutionTwo springs are joined and attached to a mass of 16 kg. The system is then suspended vertically from a rigid support. The spring constant of the two spring are k1andk2 respectively. The period of vertical oscillations of the system will be
View SolutionA 100 g mass stretches a particular spring by 9.8 cm, when suspended vertically from it. How large a mass must be attached to the spring if the period of vibration is to be 6.28 s?
View SolutionA mass m = 8kg is attached to a spring as shown in figure and held in positioin so that the spring remains unstretched. The spring constant is 200 N/m. The mass m is then released and begins to undergo small oscillations. The maximum velocity of the mass will be (g=10m/s2)
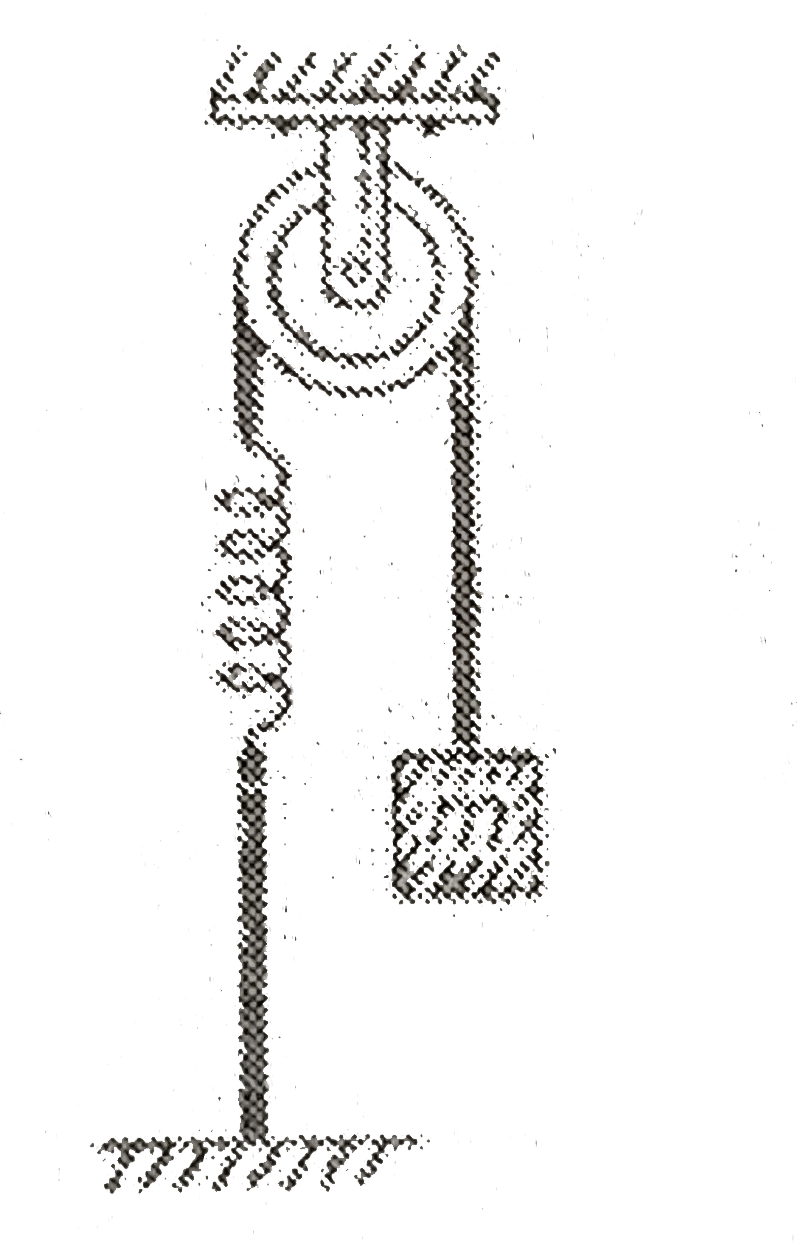
View SolutionIs oscillation of a mass suspended by a spring simple harmonic ?
View SolutionA block of mass 100g attached to a spring of stiffness 100N/m is lying on a frictionless floor as shown. The block is moved to compress the spring by 10cm and released. If the collision with the wall is elastic then find the time period of oscillations.

View Solution

