A simple pendulm has a length L and a bob of mass M. The bob is vibrating with amplitude a .What is the maximum tension in the string?
mg2
mg2[1+2(AL)2]
mg[1+(AL)2]
mg2[1+(AL)2]
The correct Answer is:C
To find the maximum tension in the string of a simple pendulum with a length L and a bob of mass M vibrating with amplitude A, we can follow these steps:
Step 1: Understand the Forces Acting on the Bob
At any point in the pendulum's swing, two main forces act on the bob:
- The gravitational force mg acting downward.
- The tension T in the string acting along the string towards the pivot.
Step 2: Identify the Components of the Gravitational Force
When the bob is at an angle θ from the vertical, the gravitational force can be resolved into two components:
- mgcosθ (along the string)
- mgsinθ (perpendicular to the string)
Step 3: Apply Newton's Second Law
Using Newton's second law in the radial direction (along the string), we have:
T−mgcosθ=mv2L
where v is the speed of the bob at that position.
Step 4: Determine the Maximum Tension
The maximum tension will occur when the bob is at the lowest point of its swing (mean position), where θ=0. Thus, we can write:
Tmax=mg+mv2L
Step 5: Calculate the Velocity at the Lowest Point
To find v2, we can use the conservation of energy. At the highest point (amplitude A), the potential energy is maximum and kinetic energy is zero. At the lowest point, potential energy is minimum and kinetic energy is maximum.
The change in height h when the bob swings from the highest point to the lowest point is:
h=L−Lcosθ0=L(1−cosθ0)
Using the small angle approximation, cosθ≈1−θ22, we can express h in terms of amplitude A:
h≈L(1−(1−A22L2))=A22L
Using conservation of energy:
mgh=12mv2
Substituting for h:
mg⋅A22L=12mv2
This simplifies to:
v2=gA
Step 6: Substitute v2 Back into the Tension Equation
Now, substituting v2 back into the tension equation:
Tmax=mg+m(gA)L
This simplifies to:
Tmax=mg+mgAL=mg(1+AL)
Final Expression
Thus, the maximum tension in the string is given by:
Tmax=mg(1+AL)
At any point in the pendulum's swing, two main forces act on the bob:
- The gravitational force mg acting downward.
- The tension T in the string acting along the string towards the pivot.
When the bob is at an angle θ from the vertical, the gravitational force can be resolved into two components:
- mgcosθ (along the string)
- mgsinθ (perpendicular to the string)
Using Newton's second law in the radial direction (along the string), we have:
T−mgcosθ=mv2L
where v is the speed of the bob at that position.
The maximum tension will occur when the bob is at the lowest point of its swing (mean position), where θ=0. Thus, we can write:
Tmax=mg+mv2L
To find v2, we can use the conservation of energy. At the highest point (amplitude A), the potential energy is maximum and kinetic energy is zero. At the lowest point, potential energy is minimum and kinetic energy is maximum.
h=L−Lcosθ0=L(1−cosθ0)
Using the small angle approximation, cosθ≈1−θ22, we can express h in terms of amplitude A:
h≈L(1−(1−A22L2))=A22L
mgh=12mv2
Substituting for h:
mg⋅A22L=12mv2
This simplifies to:
v2=gA
Now, substituting v2 back into the tension equation:
Tmax=mg+m(gA)L
This simplifies to:
Tmax=mg+mgAL=mg(1+AL)
Thus, the maximum tension in the string is given by:
Tmax=mg(1+AL)
Topper's Solved these Questions
- MOCK TEST 3BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 3EXERCISE - PART I : PHYSICS (SECTION-2)
10 Videos
- MOCK TEST 2BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 2EXERCISE - PART I : PHYSICS (SECTION - 2)
10 Videos
- MOCK TEST 4BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 4EXERCISE - PHYSICS (SECTION 2)
5 Videos
Similar Questions
A simple pendulum having a bob of mass m under goes small oscillations with amplitude θ0 Find the tension in the string as a function of the angle made by the string with the vertical. When in this tension maximum, and when is it minimum?
View SolutionA simple pendulum has a bob of mass m and swings with an angular amplitude ϕ. The tension in thread is T. At a certain time the string makes an angle θ with the vertical (θ≤ϕ)
View SolutionThe bob of a simple pendulum of length 1 m has mass 100 g and a speed of 1.4 m/s at the lowest point in its path. Find the tension in the stirng at this instant.
View SolutionA simple pendulum of length 1 m with a bob of mass m swings with an angular amplitude 30∘. Then (g=9.8m/s2
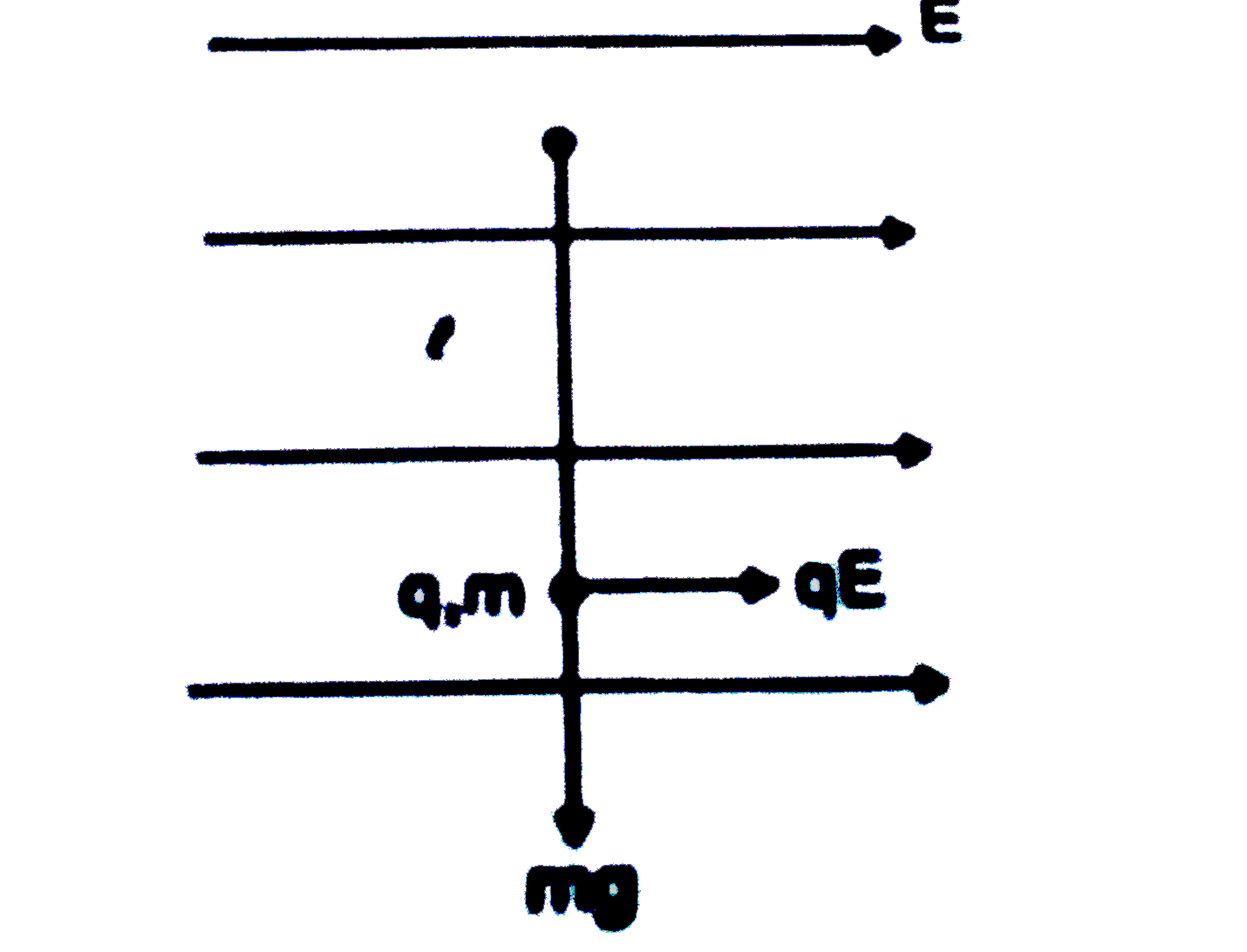
View SolutionA simple pendulum has a length l & mass of bob m. The bob is given a charge q coulomb. The pendulum is suspended in a uniform horizontal electric field of strength E as shown in figure, then calculate the time period of oscillation when bob is slightly displaced from its mean position.
View SolutionA simple pendulum with a bob of mass m swings with an angular amplitude of 40∘. When its angular displacement is 20∘, the tension in the string is greater than mgcos20∘
View SolutionA simple pendulum with a bob of mass m swings with an angular amplitude of 40∘. When its angular displacement is 20∘, the tension in the string is greater than mgcos20∘ true
false
View SolutionThe angular amplitude of a simple pendulum is θ0. The maximum tension in its string will be
View SolutionA simple pendulum of length l and bob of mass m is displaced from its equilibrium position O to a position P so that hight of P above O is h . If is then released. What is the tension in the string when the bob passes through the through the equilibrium position O ? Neglect friction. v is the velocity of the bob at O
View SolutionA simple pendulum of length L and mass (bob) M is oscillating in a plane about a vertical line between angular limit −ϕ and +ϕ. For an angular displacement θ(|θ|<ϕ), the tension in the string and the velocity of the bob are T and V respectively. The following relations hold good under the above conditions:
View Solution
