A simple pendulum of length l and mass m free to oscillate in vertical plane. A nail is located at a distance d=l−a vertically below the point of suspension of a simple pendulum. The pendulum bob is released from the position where the string makes an angle of 90∘ from vertical. Discuss the motion of the bob if (a) l=2a and (b) l=2.5a.
To solve the problem, we will analyze the motion of a simple pendulum bob released from a vertical position (90 degrees from the vertical) and how it behaves when it encounters a nail located below the point of suspension. We will consider two cases based on the given lengths of the pendulum.
Given:
- Length of pendulum: l
- Mass of pendulum bob: m
- Distance from the point of suspension to the nail: d=l−a
Case (a): l=2a
1. Initial Position: The pendulum bob is released from the position where the string is vertical. At this point, the height h from the lowest point to the release point is equal to l (which is 2a).
2. Using Work-Energy Theorem: The work done by gravity as the bob falls from the release point to the lowest point is equal to the change in kinetic energy.
W=mgh=mg(2a)=2mga
The initial kinetic energy is zero (since it starts from rest), so:
2mga=12mv2
Simplifying, we find:
v2=4ga⇒v=√4ga
3. Motion After Hitting the Nail: When the pendulum bob reaches the lowest point, it will have a speed of v=√4ga. The distance from the nail to the bob is a (since l=2a and d=l−a=a). The bob will now perform circular motion with radius a.
4. Condition for Circular Motion: For the bob to complete the circular motion, the speed must be greater than or equal to √5ga. Since √4ga<√5ga, the bob will not complete the circular motion and will fall off in a projectile motion path.
Conclusion for Case (a):
The bob will perform a combination of circular motion and projectile motion after hitting the nail.
---
Case (b): l=2.5a
1. Initial Position: The pendulum bob is again released from the vertical position, where the height h from the lowest point to the release point is l=2.5a.
2. Using Work-Energy Theorem: The work done by gravity as the bob falls is:
W=mgh=mg(2.5a)=2.5mga
Setting this equal to the change in kinetic energy:
2.5mga=12mv2
Simplifying gives:
v2=5ga⇒v=√5ga
3. Motion After Hitting the Nail: The distance from the nail to the bob is d=l−a=2.5a−a=1.5a. The bob will now perform circular motion with radius a.
4. Condition for Circular Motion: The speed of the bob at the lowest point is v=√5ga. Since this speed is equal to the required speed to complete the circular motion, the bob will complete the circular motion around the nail.
Conclusion for Case (b):
The bob will perform complete circular motion around the nail.
---
Summary:
- Case (a): l=2a leads to a combination of circular and projectile motion after hitting the nail.
- Case (b): l=2.5a allows the bob to complete circular motion around the nail.
- Length of pendulum: l
- Mass of pendulum bob: m
- Distance from the point of suspension to the nail: d=l−a
2. Using Work-Energy Theorem: The work done by gravity as the bob falls from the release point to the lowest point is equal to the change in kinetic energy.
W=mgh=mg(2a)=2mga
The initial kinetic energy is zero (since it starts from rest), so:
2mga=12mv2
Simplifying, we find:
v2=4ga⇒v=√4ga
The bob will perform a combination of circular motion and projectile motion after hitting the nail.
2. Using Work-Energy Theorem: The work done by gravity as the bob falls is:
W=mgh=mg(2.5a)=2.5mga
Setting this equal to the change in kinetic energy:
2.5mga=12mv2
Simplifying gives:
v2=5ga⇒v=√5ga
The bob will perform complete circular motion around the nail.
- Case (a): l=2a leads to a combination of circular and projectile motion after hitting the nail.
- Case (b): l=2.5a allows the bob to complete circular motion around the nail.
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective
23 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.3
26 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A pendulum has time period T for small oscillations. An obstacle P is situated below the point of suspension O at a distance 3l4. The pendulum is released from rest. Throughout the motion, the moving string makes small angle with vertical. Time after which the pendulum returns back to its initial position is
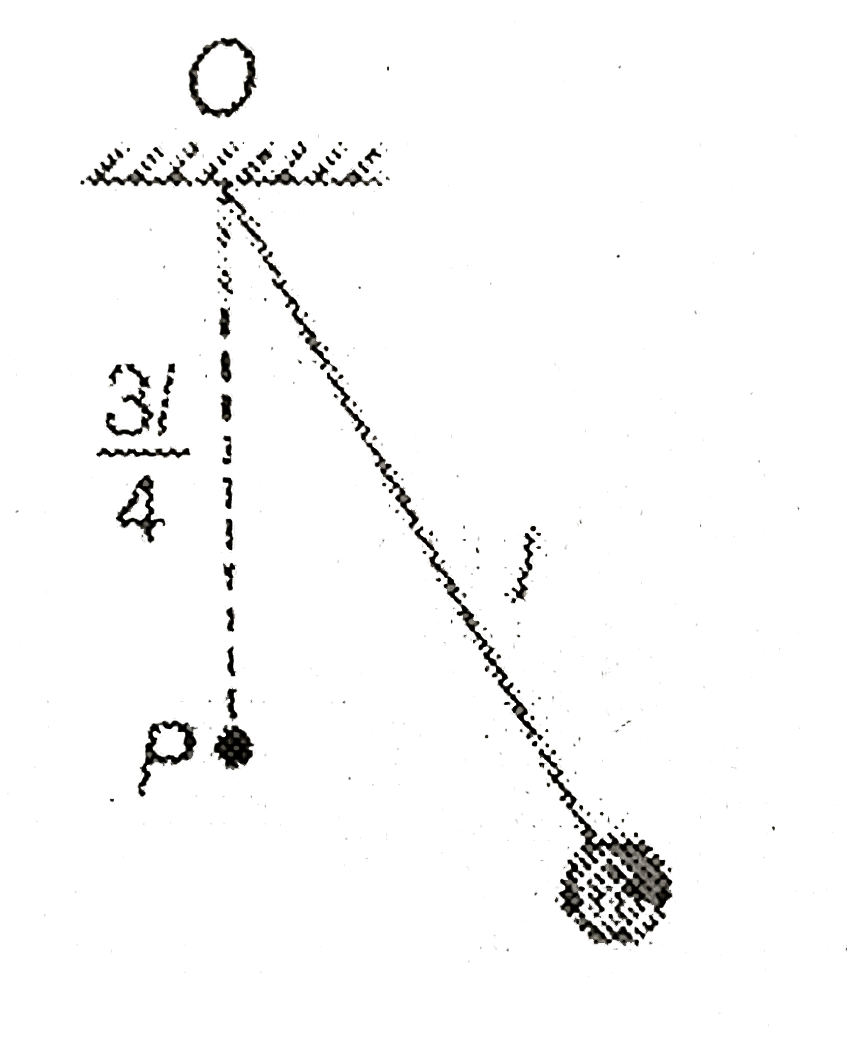
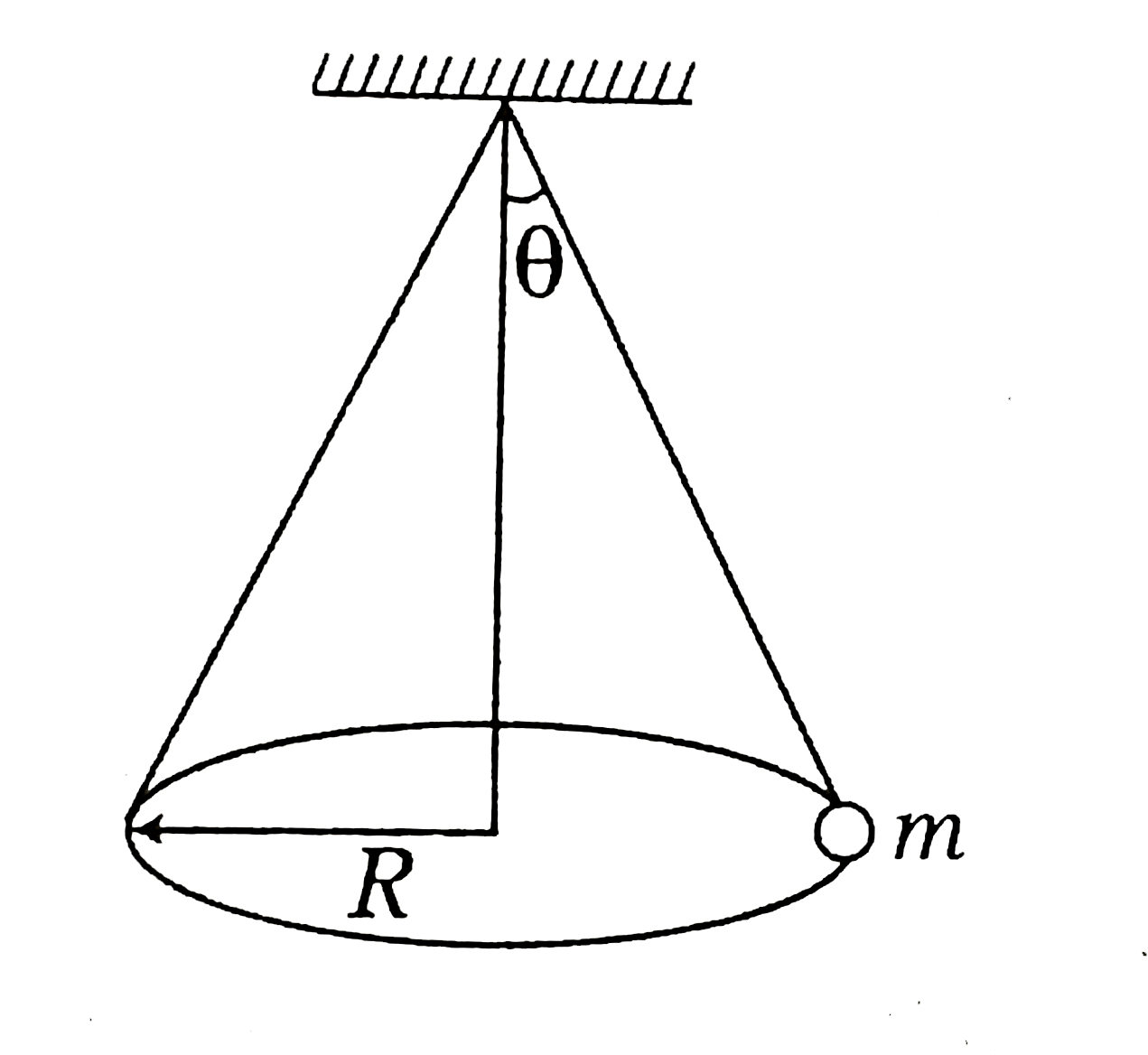
View SolutionA conical pendulum of length L makes an angle θ with the vertical. The time period will be
View SolutionA pendulum bob has a speed of 3ms−1 at its lowest position. The pendulum is 0.5 m long. The speed of the bob, when string makes an angle of 60∘ to the vertical is (take, g=10ms−1)
View SolutionA simple pendulum of length 'L' has mass 'M' and it oscillates freely with amplitude A, Energy is
(g = acceleration due to gravity)
View SolutionA simple pendulum of length l and mass m is initially at its lowest position. It is given the minimum horizontal speed necessary after to move in a circular path about the point of suspension. The tension in the string at the lowest positive of the bob is
View SolutionA bob hangs from a rigid support by an inextensible string of length l. It is released from rest when string makes an agngle 60∘ with vertical . The speed of the bob at the lowest position is
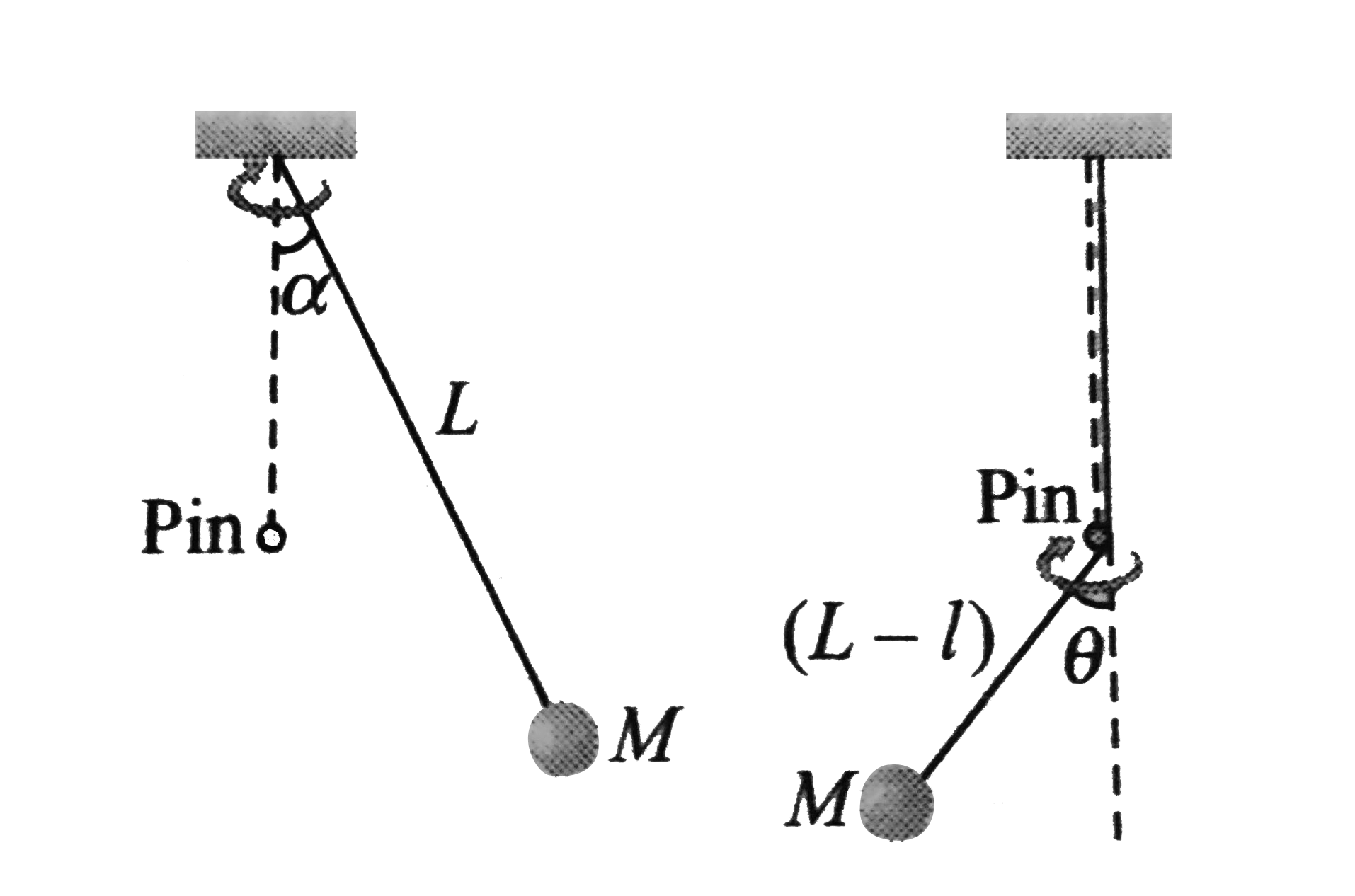
View SolutionA simple pendulum consisting of a mass M attached to a string of length L is released from rest at an angle α. A pin is located at a distance l below the pivot point. When the pendulum swings down, the string hits the pin as shown in figure. The maximum angle θ which the string makes with the vertical after hitting the pin is
View SolutionWhat is the torque acting on the bob of mass m of a simple pendulum Of length l, when the string of the pendulum makes an angle θ with the vertical ? When is the torque (i) zero and (ii) maximum.
View SolutionA simple pendulum of length l is pulled aside to make an angle θ with the vertical. Find the magnitude of the torque of the weight w of the bob about the point of suspension. When is the torque zero?
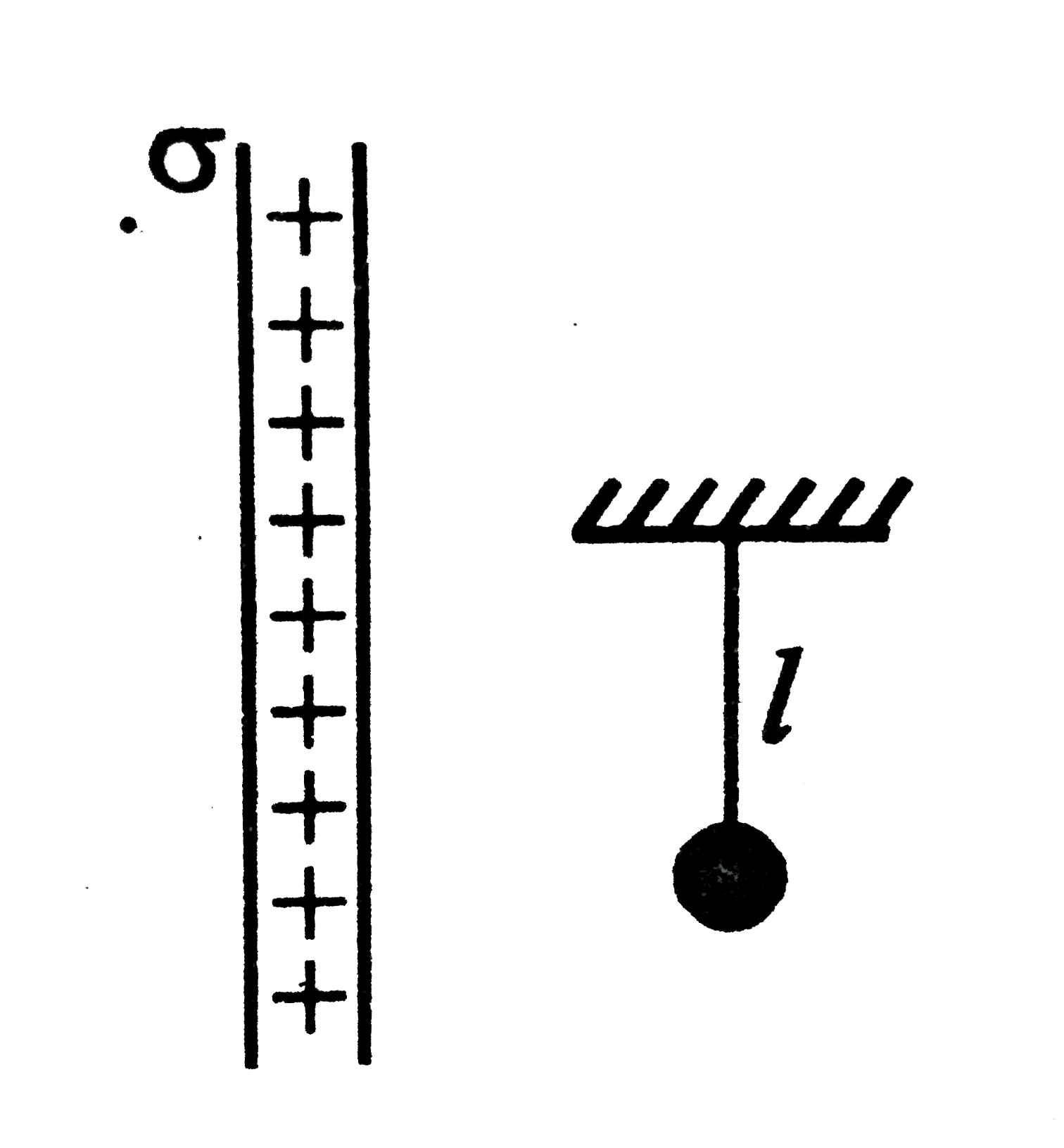
View SolutionA simple pendulum of length l and bob mass m is hanging in front of a large nonconducting sheet having surface charge density σ. If suddenly a charge +q is given to the bob & it is released from the position shown in figure. Find the maximum angle through which the string is deflected from vertical .
 .
.
View Solution
