A particle is suspended from a fixed point by a string of lengh 5m. It is projected from the equilibrium position with such a velocity that the string slakens after the particle has reached a height 8m above lowest point. Find the velocity of the particle, just before the string slackens.
Find also, to what to what height the particle can rise further?
To solve the problem step by step, we will use the principles of circular motion and projectile motion.
Step 1: Understanding the Problem
We have a particle suspended by a string of length 5 m. The particle is projected from the equilibrium position and reaches a height of 8 m above the lowest point before the string slackens. We need to find the velocity of the particle just before the string slackens and the maximum height it can reach after that.
Step 2: Determine the Effective Length of the String
When the particle reaches a height of 8 m, the vertical distance from the lowest point to the particle is 8 m. The length of the string is 5 m, so the distance from the point where the string is attached to the particle is given by:
Vertical distance from the lowest point=Length of string+Height above lowest point
Effective Length=5m−8m=−3m
Since the string cannot be negative, we need to consider the geometry of the situation. The particle is actually at a height of 3 m above the point of suspension when the string slackens.
Step 3: Using Trigonometry to Find the Angle
Using the right triangle formed by the string and the vertical height, we can find the angle θ at which the string slackens. The height above the lowest point is 3 m (5 m - 2 m).
Using the sine function:
sin(θ)=oppositehypotenuse=35
Thus,
θ=sin−1(35)≈37∘
Step 4: Applying Forces Just Before the String Slacks
At the point just before the string slackens, the forces acting on the particle are the weight (mg) and the tension (T) in the string. The centripetal force required for circular motion is provided by the component of the weight acting towards the center of the circular path.
Using the equation:
T+mgcos(53∘)=mv2r
Since the string slackens, T = 0:
mgcos(53∘)=mv2r
Where r is the radius of the circular path, which is the length of the string (5 m).
Step 5: Solving for Velocity
Cancelling m from both sides:
gcos(53∘)=v25
Substituting g=9.8m/s2 and cos(53∘)≈0.6:
9.8×0.6=v25
v2=9.8×0.6×5
v2=29.4
v=√29.4≈5.42m/s
Step 6: Finding Maximum Height After Slackening
Once the string slackens, the particle will follow a projectile motion. The maximum height (h) reached after slackening can be calculated using the formula:
h=v2sin2(θ)2g
Where sin(53∘)≈0.8:
h=(5.42)2×(0.8)22×9.8
Calculating:
h=29.4×0.6419.6
h≈0.96m
Final Answers
1. The velocity of the particle just before the string slackens is approximately 5.42 m/s.
2. The maximum height the particle can rise further is approximately 0.96 m.
We have a particle suspended by a string of length 5 m. The particle is projected from the equilibrium position and reaches a height of 8 m above the lowest point before the string slackens. We need to find the velocity of the particle just before the string slackens and the maximum height it can reach after that.
When the particle reaches a height of 8 m, the vertical distance from the lowest point to the particle is 8 m. The length of the string is 5 m, so the distance from the point where the string is attached to the particle is given by:
Effective Length=5m−8m=−3m
Using the right triangle formed by the string and the vertical height, we can find the angle θ at which the string slackens. The height above the lowest point is 3 m (5 m - 2 m).
sin(θ)=oppositehypotenuse=35
Thus,
θ=sin−1(35)≈37∘
At the point just before the string slackens, the forces acting on the particle are the weight (mg) and the tension (T) in the string. The centripetal force required for circular motion is provided by the component of the weight acting towards the center of the circular path.
T+mgcos(53∘)=mv2r
Since the string slackens, T = 0:
mgcos(53∘)=mv2r
Where r is the radius of the circular path, which is the length of the string (5 m).
Cancelling m from both sides:
gcos(53∘)=v25
Substituting g=9.8m/s2 and cos(53∘)≈0.6:
9.8×0.6=v25
v2=9.8×0.6×5
v2=29.4
v=√29.4≈5.42m/s
Once the string slackens, the particle will follow a projectile motion. The maximum height (h) reached after slackening can be calculated using the formula:
h=v2sin2(θ)2g
Where sin(53∘)≈0.8:
h=(5.42)2×(0.8)22×9.8
Calculating:
h=29.4×0.6419.6
h≈0.96m
1. The velocity of the particle just before the string slackens is approximately 5.42 m/s.
2. The maximum height the particle can rise further is approximately 0.96 m.
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective
23 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.3
26 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A particle suspended from a fixed point, by a light inextensible thread of length L is projected horizontally from its lowest position with velocity 7gL . The thread will slack after swinging through an angle , such that equal
View SolutionA particle suspended by a light inextensible thread of length l is projected horizontally from its lowest position with velocity √7gl/2. The string will slack after swinging through an angle equal to
View SolutionA heavy particle hangs from a point O, by a string of length a. It is projected horizontally with a velocity u=√(2+√3)ag . The angle with the downward vertical, string makes where string becomes slack is :
View SolutionA particle of mass m attached to a string of length l is descending circular motion on a smooth plane inclined at an angle α with the horizontal. For the particle to reach the highest point its velocity at the lowest point should exceed.
View SolutionA particle is projected from a point on the level ground and its height is h when at horizontal distances aand2a from its point of projection. Find the velocity of projection.
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizonally with speed √gl . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
View SolutionA particle is projected from the ground at an angle such that it just clears the top of a polar after t1 time its path. It takes further t2 time to reach the ground. What is the height of the pole ?
View SolutionA particle of mass m is attached to a string of length L and given velocity √10gL in the horizontal direction at the lowest point. Find tension in the string when the particle is at (i) lowest position (ii) highest position,
View SolutionA particle of mass 1kg is attached to a string of length 5m. The string is attached to a fixed point O. It is released from theposition as shown in Fig. Calculate
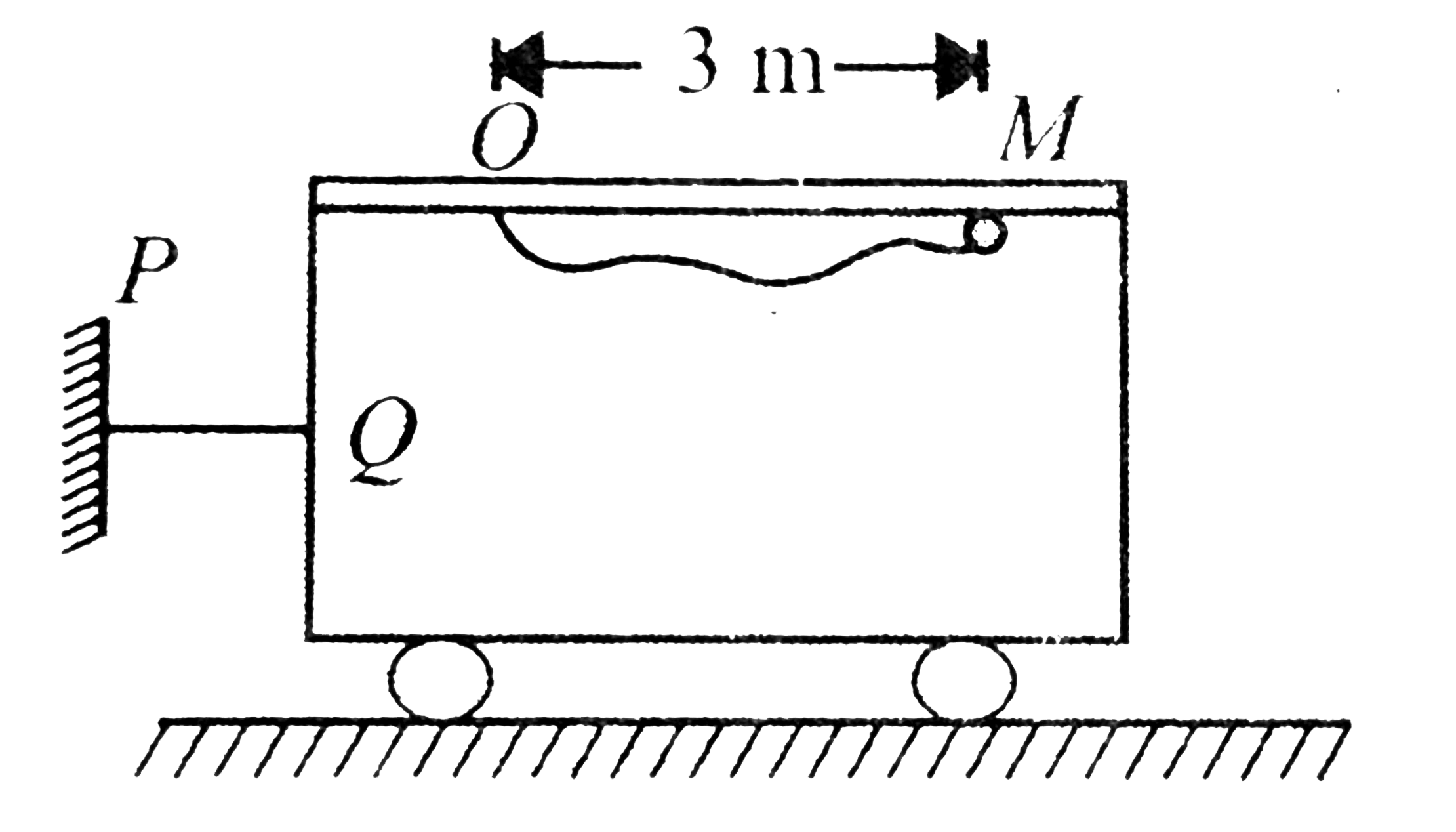
a. the impulse developed in the string when it becorries taut,
b. the velocity of the particle just after the string becomes taut,
c. the impulse developed in this string PQ at this instant.
View Solution
