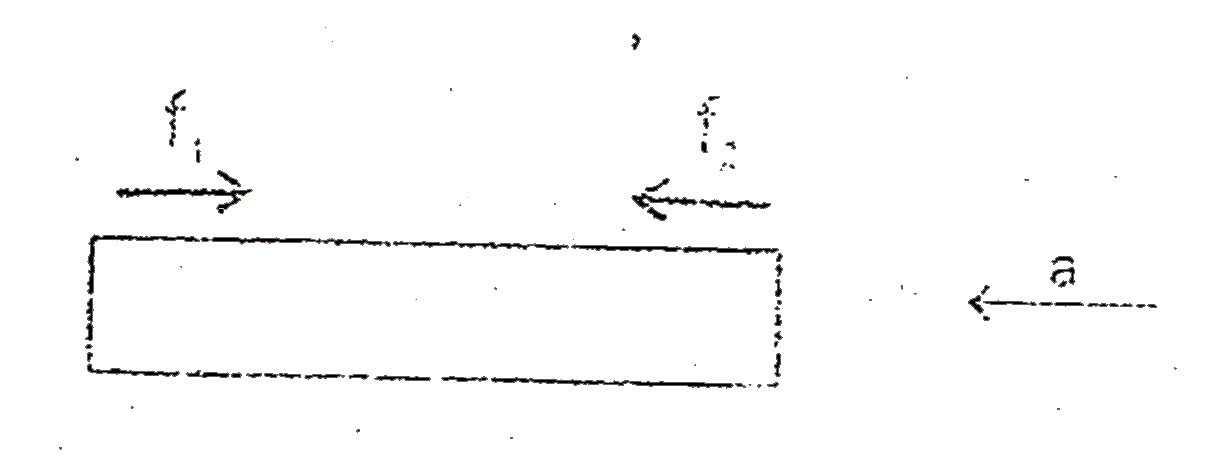
Two wheels which are rotated by some external source with constant angular velocity in opposite directions as shown in figure. A uniform plank of mass M is placed on it symmetrically. The friction co-efficient between each wheel and the plank is μ. find the frequency of oscillations, when plank is slightly displaced along its length and released.

The correct Answer is:2π√lμg
If plank is displaced by x toward right then

Let N1,N2 and f1,f2 are Normal and friction force at Point A and B by force balance
N1+N2=Mg1
amd Torque balance
Mg(l+X)=N2×2l_(2)
by equation (1) and (2)
N1=Mg2−Mgx2l,N2=Mg2+Mgx2l
So f1=μ(Mg2−Mgx2l)
and f2=μ(Mg2+Mgx2l)
F.B.D of M
f2−f1=Ma
μ.2Mgx2l=Ma=−d2xdt2.M
⇒d2xdt2=−μgxl
Time period =2π√lμg
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 3, PART - II
Explore 17 Videos
- SEMICONDUCTORSBook:RESONANCE ENGLISHChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PHYSICS
Explore 784 Videos
Similar Questions
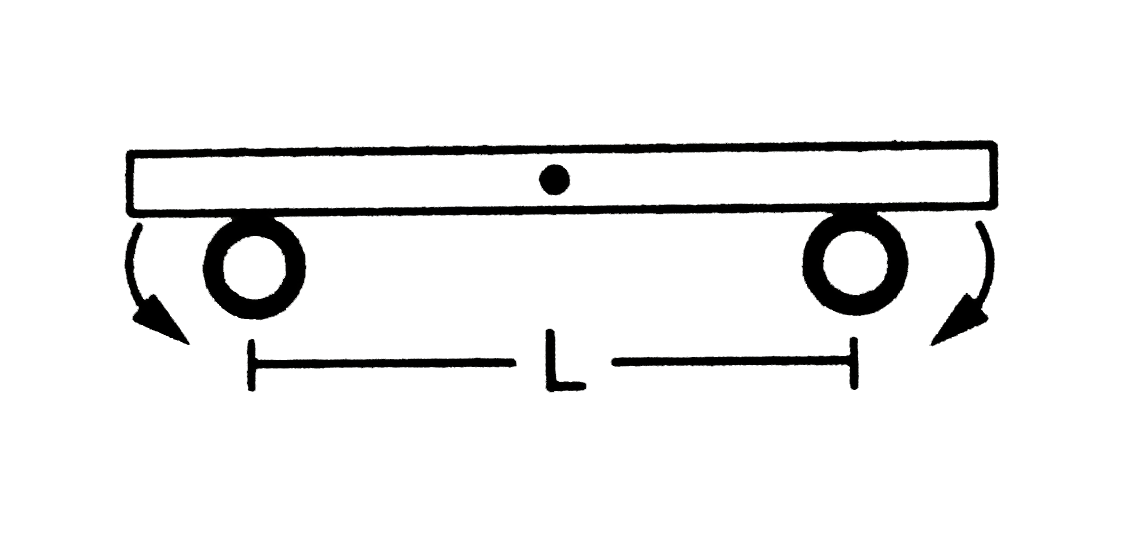
A uniform table of mas M stays horizontally and symmetrically on two wheels rotatig in opposite directions figure. The separsation between the wheels is L. The friction coefficeint between each whee, and the plate is μ. Find the time period of oscilationof the pate if it is slightly displaced along its length and released.
View SolutionA block of mass m=2kg of shown dimensions is placed on a plank of mass M = 6Kg which is placed on smooth horizontal plane. The coefficient of friction between the block and the plank is μ=13. If a horizontal froce F is applied on the plank, then find the maximum value of F (in N) for which the block and the plank move together

View SolutionA disc of radius R rotates from rest about a vertical axis with a constant angular acceleration such that a coin placed with a tangenitial between a as shown in figure If the coefficient of static friction between the coin and disc is μs .Find the velocity of the before it start sliding relative as the disc

View SolutionA disc of radius R rotates from rest about a vertical axis with a constant angular acceleration such that a coin placed with a tangenitial between a as shown in figure If the coefficient of static friction between the coin and disc is μs .Find the velocity of the before it start sliding relative as the disc

View SolutionA uniform horizontal plank is resting symmetrically in a horizontal position on two cylindrical droms , which are apinning in in opposite direction about their horizontal axes with equal angular velocity . The distance between the axes with equal angular velocity. The distance between the axes is 2L and the coefficient of friction between the plank and cylender is μ . If the plank is displaced slightly from the equilibrium position along its length and released, show that it performs simple horizontal motion. Caculate also the time period of motion.
View Solution
The kinetic energy of a uniform rod of mass m rotating with constant angular velocit ω about one of its end which is fixed as shown in figure is mω2l2N find N
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.
View SolutionFigure shown a small block A of mass m kept at the left end of a plank B of mass M=2m and length l . The system can slide on a horizontal road. The system is started towards right with the initial velocity v. The friction coefficient between the road and the plank is 1/2 and that between the plank and the block is 1/4 . Find

(a) the time elapsed before the block separates from the plank
(b) displacement of block and plank relative to ground till that moment.
View SolutionA block of mass m is pushed with a velocity v0 along the surface of a trolley car of mass M. If the horizontal ground is smooth and the coefficient of kinetic friction between the block of plank is μ. Find the minimum distance of relative sliding between the block and plank.

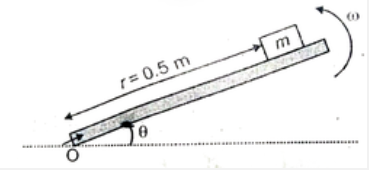
View SolutionA wooden plank OA rotates in vertical plane about horizontal axis through O with a constant angular velocity ω=3rad/s . As it passes the position θ=0 , a small mass m is placed upon it at a radial distance r=0⋅5 m . If the mass m starts sliding at θ=37∘ , find the coefficient of friction between mass and the plane .
View Solution

