
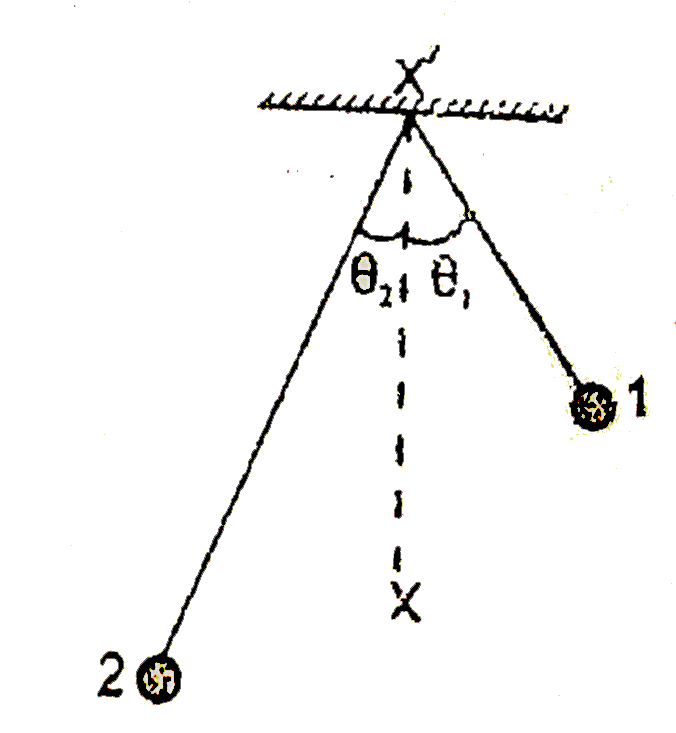
Two simple pendulums A and B having lengths l and l4 respectively are released from the position as shown in Fig. Calculate the time (in seconds) after which the two strings become parallel for the first time. (Take l=90π2m and g=10ms2),θ(1)=θ(2).
The correct Answer is:π3√lg
The angular position of pendulum 1 and 2 are (taking angles to the right of reference line ×' to be positive)
θ1=θcos(4πTt), [where T=2π√lg]
θ2=−θcos(2πT)t=cos(2πTt+π)
F for the strings to be parallel for the first time
or cos(4πTt)=cos(2πTt+π) ltbr> ∴4πTt=2nπ±(2πTt+π)
for n=0,t=T2
for n=1,t=T6,3T2
∴ Both the pendulum are parallel to each other for the first time after t=T6=√lg
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 3, PART - II
Explore 17 Videos
- SEMICONDUCTORSBook:RESONANCE ENGLISHChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PHYSICS
Explore 784 Videos
Similar Questions
Two simple pendulum have lengths land 25l16 . At t=0 they are in same phase after how may oscillations of smaller pendulum will they be again in phase for first time ?
View SolutionTwo simple pendulum of length l and 16l are released from the same phase together. They will be at the same time phase after a minimum time.
View Solution
Knowledge Check
Two plane mirrors M1 and M2 are inclined at angle as shown in Figure . A ray of light1, which is parallel to M1 , strike M2 and after two reflections, ray 2 becomes parallel to M2. Find the angle θ .
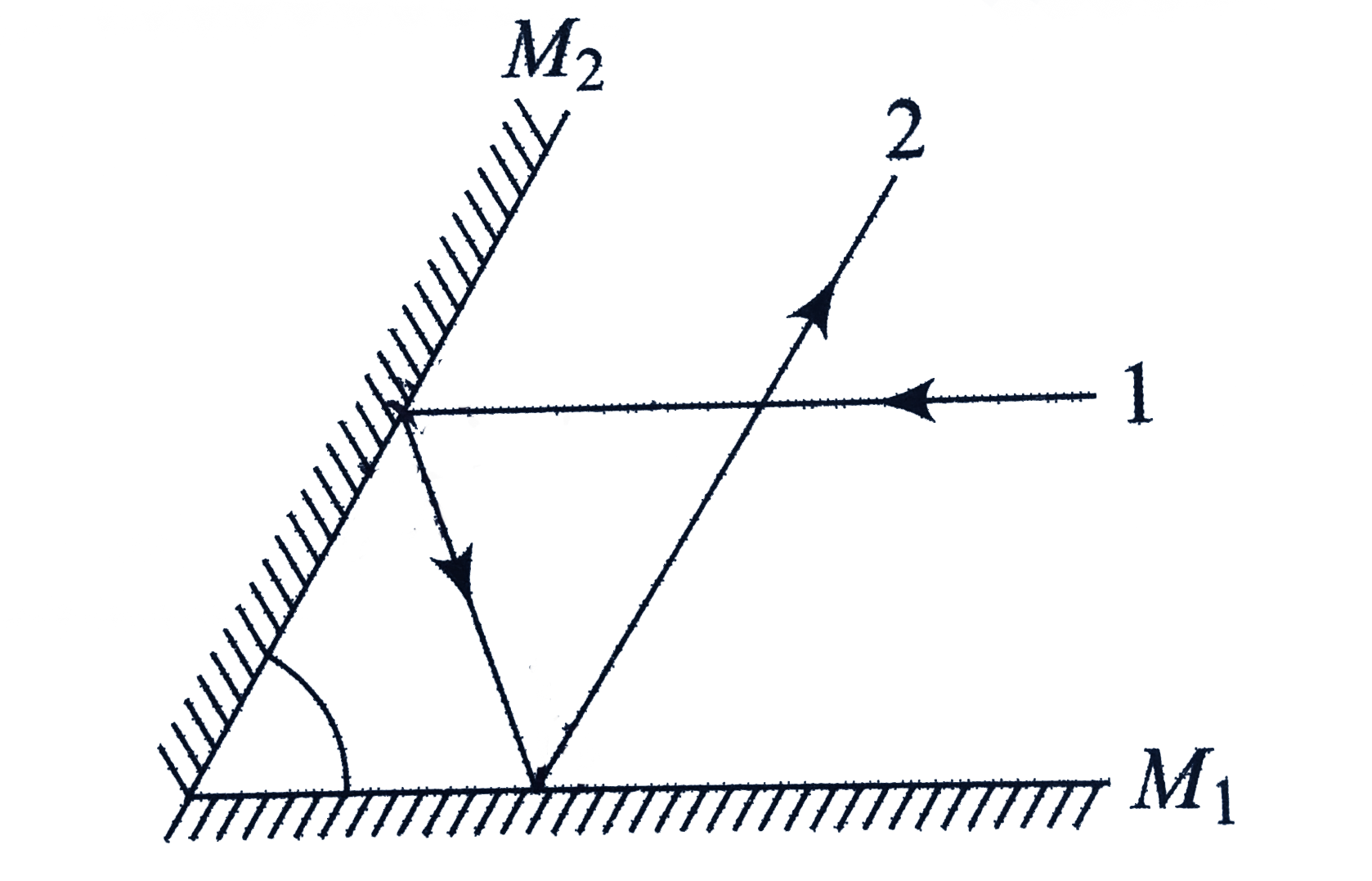 A0∘B30∘C45∘D60∘
A0∘B30∘C45∘D60∘
A uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View SolutionThere are two pendulums with bobs having indencital size and mass. The pendulum A is released from rest in the position as shown in the figure. If the maximum angle formed by cord BO' with vertical in the subsequent motion of sphere B is equal to the angle θ0 If the coefficient of restitution between sphere A and sphere B is l. find

a. the velocities of sphere A and sphere B just after collisions
b. the ratio of lengths of pendulums lB/lA.
View SolutionTwo identical simple pendulums A and B are fixed at same point. They are displaced by very small angles α and β(β>α) and released from rest. Find the time after which B reaches its initial position for the first time. Collisions are elastic and length of strings is l.

View SolutionA simple pendulum consisting of a mass M attached to a string of length L is released from rest at an angle α. A pin is located at a distance l below the pivot point. When the pendulum swings down, the string hits the pin as shown in figure. The maximum angle θ which the string makes with the vertical after hitting the pin is

View SolutionThe bob of a simple pendulum of length L is released at time t = 0 from a position of small angular displacement θ0 . Its linear displacement at time t is given by :
View SolutionA pendulum suspended from the ceiling of the train has a time period of two seconds when the train is at rest, then the time period of the pendulum, if the train accelerates 10 m/s2 will be (g=10m/s2)
View SolutionA simple pendulum is taken at a place where its separation from the earth's surface is equal to the radius of the earth. Calculate the time period of small oscillation if the length of the string is 1.0m. Take g=π2m/s2 at the surface of the earth.
View Solution

