A simple pendulum is constructed by hanging a heavy ball by a 5.0 long string. It undergoes small oscillation. a. How many oscillations does it make per second? b. What will be the frequency if the system is taken on the moon where acceleration due to gravitation of the moon is 1.67ms−2?
The correct Answer is:A, B, C
L=5m
a. T=2π√lg
=2π√510
=2π√0.5=2π(0.7)
In 2π(0.7)sec, the body will complete 12π(.7) oscillation
∴f=12π(0.7)
=1014π=0.71π times
b. When it is taken to the moon
T=2π√(lg)
Where g is Acceleration on the moon
=2π√51.67
f=1T 12π√1.675=12π(0.557)
=12π√3
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
15 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
Similar Questions
A simple seconds pendulum is constructed out of a very thin string of thermal coefficient of linear expansion α=20×10−4/∘C and a heavy particle attached to one end. The free end of the string is suspended from the ceiling of an elevator at rest. the pendulum keeps correct time at 0∘C. when the temperature rises to 50∘C, the elevator operator of mass 60kg being a student of Physics accelerates the elevator vertically, to have the pendulum correct time. the apparent weight of the operator when the pendulum keeps correct time at 50∘C is (Take g=10m/s2)
View SolutionA simple pendulum is being used to determine the value of gravitational acceleration g at a certain place. The length of the pendulum is 25.0 cm and a stop watch with 1 s resolution measures the time taken for 40 oscillations to be 50 s. The accuracy in g is:
View SolutionAn almost inertia-less rod of length l3.5 m can rotate freely around a horizontal axis passing through its top end. At the bottom end of the roa a small ball of mass m andat the mid-point another small ball of mass 3m is attached. Find the angular frequency (in SI units) of small oscillations of the system about the equilibrium position. Gravitational acceleration is g=9.8 m//s^(2).

View Solution
The approximate height h of an object launched vertically upward after an elapsed time t is represented by the equation h=12at2+vot+ho, where a is acceleration due to gravity, vo is the object's initial velocity, and ho is the objects initial height. the table aabove gives the acceleration due to gravity on Earth's moon and several planets. If two identical objects launched vertically upward at an initial velocity of 40m/s from the surfaces of Mars and Earth's moon approximately how many more seconds will it take for the moon projectile to return to the ground than the Mars projectile?
View SolutionThe period of oscillation of a simple pendulum is given by T=2π√Lg, where L is the length of the pendulum and g is the acceleration due to gravity. The length is measured using a meter scale which has 500 divisions. If the measured value L is 50 cm, the accuracy in the determination of g is 1.1% and the time taken for 100 oscillations is 100 seconds, what should be the possible error in measurement of the clock in one minute (in milliseconds) ?
View SolutionA simple pendulum is taken at a place where its separation from the earth's surface is equal to the radius of the earth. Calculate the time period of small oscillation if the length of the string is 1.0m. Take g=π2m/s2 at the surface of the earth.
View SolutionA simple pendulum of length l and mass m free to oscillate in vertical plane. A nail is located at a distance d=l−a vertically below the point of suspension of a simple pendulum. The pendulum bob is released from the position where the string makes an angle of 90∘ from vertical. Discuss the motion of the bob if (a) l=2a and (b) l=2.5a.
View SolutionIn an oscillating L−C circuit in which C=4.00μF, the maximum potential difference capacitor during the oscillations is 1.50V and the maximum current through 50.0mA.
(a) What is the inductance L?
(b) What is the frequency of the oscillations?
(c) How much time does the charge on the capacitor take to rise from zero to its maximum value?
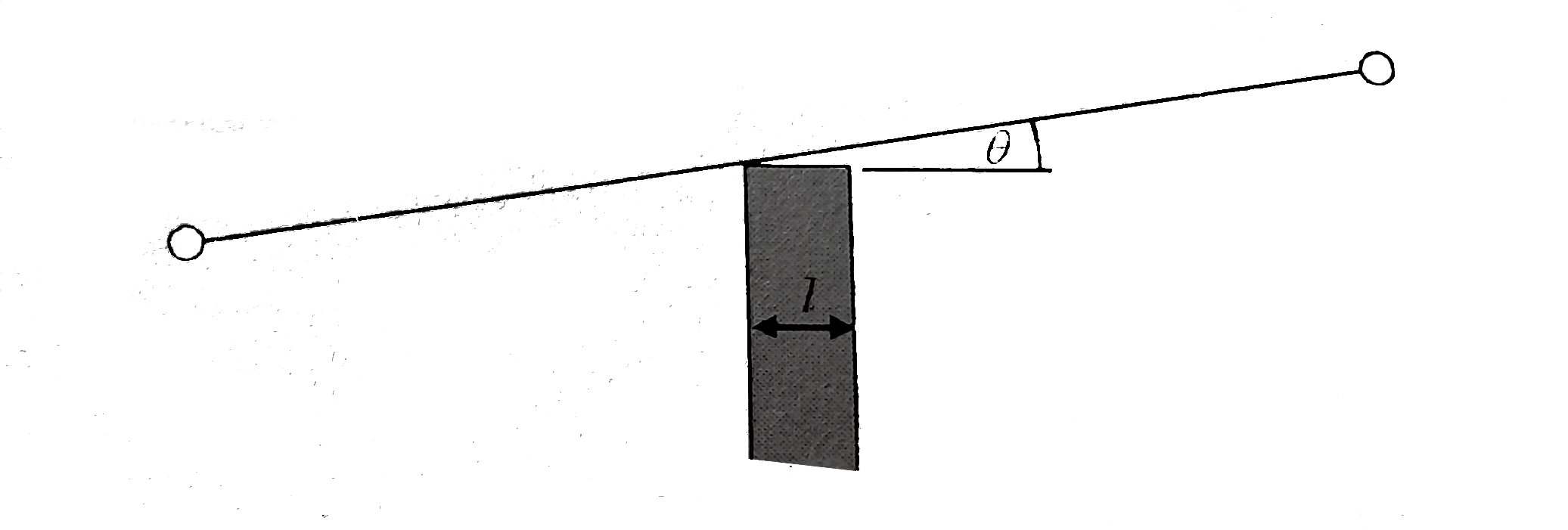
View SolutionTwo identical small balls each of mass m are rigidly affixed at the ends of light rigid rod of length 1.5m and the assmebly is placed symmetrically on an elevated protrusion of width l as shown in the figure.
The rod-ball assmebly is titled by a small angle theta in the vertical plane as shown in the figure and released. Estimate time-period (in seconds) of the oscillation of the rod-ball assembly assuming collisions of the rod with corners of the protrusion to be perfectly elastic and the rod does not slide on the corners. Assume θ=gl (numerically in radians), where g is the acceleration of free fall.
View SolutionA small bar magnet having a magnitic moment of 9×10−3Am−2 is suspended at its centre of gravity by a light torsionless string at a distance of 10−2m vertically above a long, straight horizontal wire carrying a current of 1.0A from east to west. Find the frequency of oscillation of the magnet about its equilibrium position. The moment of inertia of the magnet is 6×10−9kgm2.(H=3×10−5T).
View Solution
