A uniform disc of mass m and radius r is suspended through a wire attached to its Centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
The correct Answer is:B
To find the torsional constant K of the wire when a uniform disc of mass m and radius r is suspended through it, we can follow these steps:
Step 1: Understand the formula for the time period of torsional oscillations
The time period T of torsional oscillations is given by the formula:
T=2π√IK
where I is the moment of inertia and K is the torsional constant.
Step 2: Determine the moment of inertia of the disc
For a uniform disc of mass m and radius r, the moment of inertia I about its center is given by:
I=12mr2
Step 3: Substitute the moment of inertia into the time period formula
Now, substitute the expression for I into the time period formula:
T=2π√12mr2K
Step 4: Square both sides to eliminate the square root
Squaring both sides gives:
T2=(2π)2⋅12mr2K
This simplifies to:
T2=4π2⋅12mr2K
Step 5: Rearrange to solve for K
Rearranging the equation to solve for K gives:
K=4π2⋅12mr2T2
This simplifies to:
K=2π2mr2T2
Final Result
Thus, the torsional constant K of the wire is:
K=2π2mr2T2
---
The time period T of torsional oscillations is given by the formula:
T=2π√IK
where I is the moment of inertia and K is the torsional constant.
For a uniform disc of mass m and radius r, the moment of inertia I about its center is given by:
I=12mr2
Now, substitute the expression for I into the time period formula:
T=2π√12mr2K
Squaring both sides gives:
T2=(2π)2⋅12mr2K
This simplifies to:
T2=4π2⋅12mr2K
Rearranging the equation to solve for K gives:
K=4π2⋅12mr2T2
This simplifies to:
K=2π2mr2T2
Thus, the torsional constant K of the wire is:
K=2π2mr2T2
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer15videos
SIMPLE HARMONIC MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-215videos
SIMPLE HARMONIC MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer21videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-27videos
SOME MECHANICAL PROPERTIES OF MATTER
Similar Questions
For a uniform ring of mass M and radius R at its centre
View SolutionA uniform solid sphere of mass m and radius R is suspended in vertical plane from a point on its periphery. The time period of its oscillation is
View SolutionA disc of mass 1 kg and radius 10 cm is suspended by vertical wire at its centre. If the time period is 3.2 s. Find the modulus of torison.
View SolutionA uniform semi-circular disc of mass m and radius r is suspended as shown in the figure. If T is the time period of small osciallations about an axis passing through point of supension and perpendicular to plane of disk. Then T is equal to
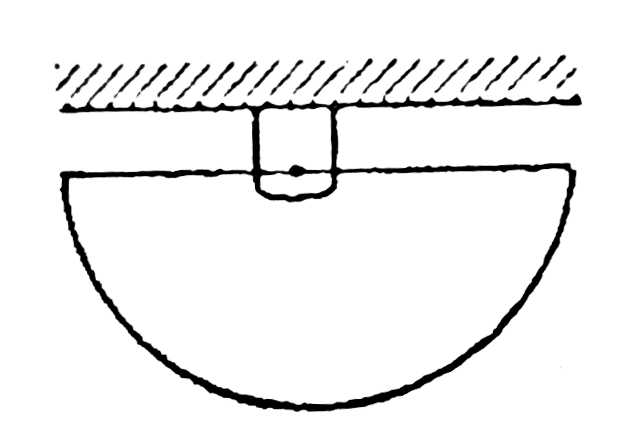 View Solution
View SolutionA uniform disc of radius 5.0 cm and mass 200g is fixed at its centre to a metal wire, the other end of which is fixed with a clamp. The hanging disc is rotated about the wire through an angle and is released. If the disc makes torsional oscillations with time period 0.20s, find the torsional constant of the wire.
View SolutionA circular disc of mass 10kg is suspended by a wire attahced to its centre. The wire is twisted by rotating the disc and released. The period of torsional oscillations is found to be 1.5s. The radius of the disc is 15cm. Determing the torsional spring constant of the wire. (Torsional spring constant α is definied by the relation J=−αθ, where J is the restoring coubple and θ the angle of twist.
View SolutionA uniform rod of mass m and length l is suspended through a light wire of length l and torsional constant k as shown in figure. Find the time perid iof the system makes a. small oscillations in the vertical plane about the suspension point and b. angular oscillations in the horizontal plane about the centre of the rod.
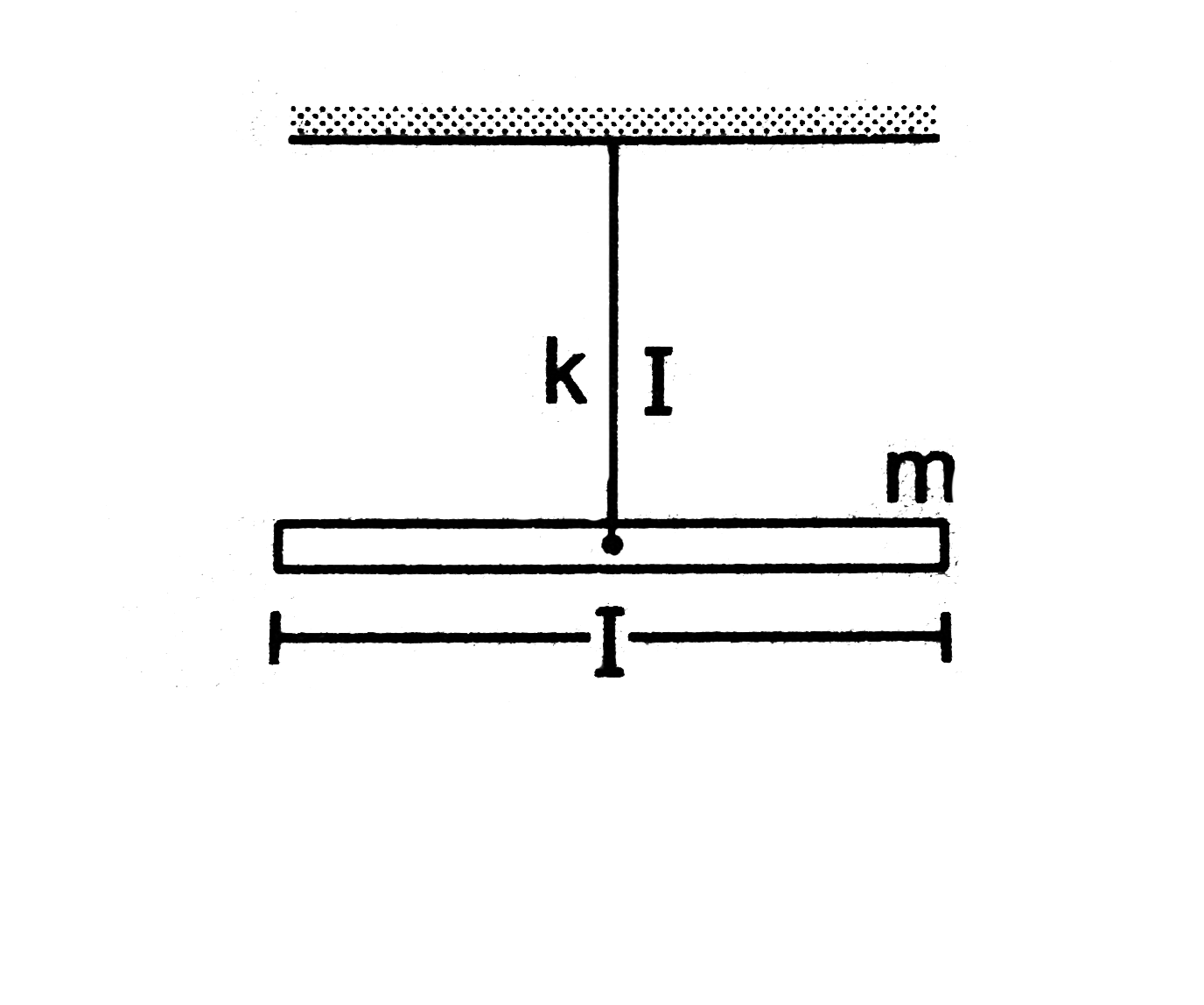 View Solution
View SolutionFind time period of uniform disc of mass m and radius r suspended through point r/2 away from centre, oscillating in a plane parallel to its plane.
View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 View Solution
View SolutionA uniform disc (of mass M and radius a) has a hole (of radius b) drilled through it. The centre of the hole is at a distance c from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?
View Solution
