A uniform disc (of mass M and radius a) has a hole (of radius b) drilled through it. The centre of the hole is at a distance c from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?
To find the moment of inertia of a uniform disc with a hole drilled through it, we can follow these steps:
Step 1: Understand the Problem
We have a uniform disc of mass M and radius a with a hole of radius b drilled through it. The center of the hole is at a distance c from the center of the original disc. We need to find the moment of inertia of the remaining part of the disc about an axis through its center and perpendicular to its plane.
Step 2: Determine the Mass of the Original Disc
The mass M of the original disc can be expressed in terms of its density σ and area:
M=σ⋅Area of the disc=σ⋅πa2
Step 3: Determine the Mass of the Removed Hole
The mass m of the removed hole can also be expressed similarly:
m=σ⋅Area of the hole=σ⋅πb2
Step 4: Relate the Masses
From the expressions for M and m, we can find the ratio of the masses:
Mm=σ⋅πa2σ⋅πb2=a2b2
Step 5: Moment of Inertia of the Original Disc
The moment of inertia I of a solid disc about an axis through its center and perpendicular to its plane is given by:
Ioriginal=12Ma2
Step 6: Moment of Inertia of the Removed Hole
To find the moment of inertia of the removed hole about the same axis, we use the parallel axis theorem:
Iremoved=Ihole, center+md2
where d=c is the distance from the center of the original disc to the center of the hole. The moment of inertia of the hole about its own center is:
Ihole, center=12mb2
Thus,
Iremoved=12mb2+mc2
Step 7: Calculate the Moment of Inertia of the Remaining Part
The moment of inertia of the remaining part of the disc is:
Iremaining=Ioriginal−Iremoved
Substituting the expressions we derived:
Iremaining=12Ma2−(12mb2+mc2)
Step 8: Substitute m in Terms of M
Using the relation m=Mb2a2 from the mass ratio, we can substitute m into the equation:
Iremaining=12Ma2−(12(Mb2a2)b2+(Mb2a2)c2)
Simplifying this gives:
Iremaining=12Ma2−(Mb42a2+Mb2c2a2)
Step 9: Final Expression
Combining the terms, we arrive at the final expression for the moment of inertia of the remaining part:
Iremaining=M2(a2−b4a2−2b2c2a2)
Final Answer
Thus, the moment of inertia of the disc about an axis through the center and perpendicular to its plane is:
I=M2(a2−b4a2−2b2c2a2)
We have a uniform disc of mass M and radius a with a hole of radius b drilled through it. The center of the hole is at a distance c from the center of the original disc. We need to find the moment of inertia of the remaining part of the disc about an axis through its center and perpendicular to its plane.
The mass M of the original disc can be expressed in terms of its density σ and area:
M=σ⋅Area of the disc=σ⋅πa2
The mass m of the removed hole can also be expressed similarly:
m=σ⋅Area of the hole=σ⋅πb2
From the expressions for M and m, we can find the ratio of the masses:
Mm=σ⋅πa2σ⋅πb2=a2b2
The moment of inertia I of a solid disc about an axis through its center and perpendicular to its plane is given by:
Ioriginal=12Ma2
To find the moment of inertia of the removed hole about the same axis, we use the parallel axis theorem:
Iremoved=Ihole, center+md2
where d=c is the distance from the center of the original disc to the center of the hole. The moment of inertia of the hole about its own center is:
Ihole, center=12mb2
Thus,
Iremoved=12mb2+mc2
The moment of inertia of the remaining part of the disc is:
Iremaining=Ioriginal−Iremoved
Substituting the expressions we derived:
Iremaining=12Ma2−(12mb2+mc2)
Using the relation m=Mb2a2 from the mass ratio, we can substitute m into the equation:
Iremaining=12Ma2−(12(Mb2a2)b2+(Mb2a2)c2)
Simplifying this gives:
Iremaining=12Ma2−(Mb42a2+Mb2c2a2)
Combining the terms, we arrive at the final expression for the moment of inertia of the remaining part:
Iremaining=M2(a2−b4a2−2b2c2a2)
Thus, the moment of inertia of the disc about an axis through the center and perpendicular to its plane is:
I=M2(a2−b4a2−2b2c2a2)
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTE ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Assignment (Section - J) Aakash Challengers Questions
Explore 13 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTE ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Try Yourself
Explore 63 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTE ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Assignment (Section - H) Multiple True-False Type Questions
Explore 4 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:AAKASH INSTITUTE ENGLISHChapter:SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:Assignment (Section-D (Assertion and reason))
Explore 5 Videos
- TEST 1Book:AAKASH INSTITUTE ENGLISHChapter:TEST 1Exercise:EXERCISE
Explore 21 Videos
Similar Questions
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionIf a circular concentric hole is made on a disc then about an axis passing through the centre of the disc and perpendicular to its plane
View SolutionRadius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
View SolutionA disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulting flat body.
View SolutionA disc of mass m and radius R, is placed on a smooth text service fixed surface . Point A is the geometrical centre of the disc while point B is the centre of mass of the disc . The moment of inertia of the dics about an axis through its centre of mass and perpendicular to the plane of the figure is I .A constant force F is applied to the top of the disc . The acceleration of the centre A of the disc at the instant B is below A (on the same vertical line ) will be :
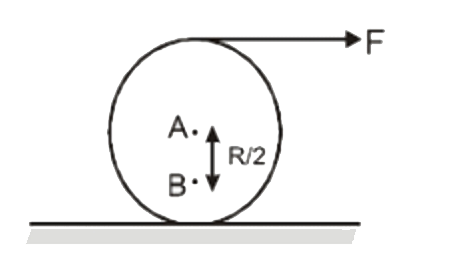
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionFive particles of mass 2 kg are attached to the rim of a circular disc of radius 0.1 m & negligible mass. Moment of inertia of the system about an axis passing through the centre of the disc & perpendicular to its plane is
View SolutionA disc of mass m and radius R has a concentric hole of radius r. Its moment of inertia about an axis through its center and perpendicular to its plane is
View Solution