A disc of mass m and radius R has a concentric hole of radius r. Its moment of inertia about an axis through its center and perpendicular to its plane is
To find the moment of inertia of a disc with a concentric hole about an axis through its center and perpendicular to its plane, we can follow these steps:
1. Understanding the System:
- We have a disc of mass m and radius R with a concentric hole of radius r. The moment of inertia (I) we want to calculate is for the entire disc minus the hole.
2. Consider a Differential Ring:
- Imagine taking a thin ring of thickness dx at a distance x from the center of the disc. The area of this ring can be expressed as:
\(
dA = 2\pi x \, dx
\)
3. Mass per Unit Area:
- The mass per unit area (σ) of the disc can be calculated as:
\(
\sigma = \frac{m}{\text{Area of the disc}} = \frac{m}{\pi (R^2 - r^2)}
\)
- The area of the disc is the area of the larger circle minus the area of the hole.
4. Mass of the Differential Ring:
- The mass of the differential ring (dm) can be expressed as:
\(
dm = \sigma \cdot dA = \sigma \cdot 2\pi x \, dx
\)
5. Moment of Inertia of the Differential Ring:
- The moment of inertia of this ring about the center is given by:
\(
dI = dm \cdot x^2 = \sigma \cdot 2\pi x \, dx \cdot x^2 = 2\pi \sigma x^3 \, dx
\)
6. Integrate to Find Total Moment of Inertia:
- We need to integrate dI from r to R (the limits of the ring):
\(
I = \int_{r}^{R} 2\pi \sigma x^3 \, dx
\)
- Performing the integration:
\(
I = 2\pi \sigma \left( \frac{x^4}{4} \right)_{r}^{R} = 2\pi \sigma \left( \frac{R^4}{4} - \frac{r^4}{4} \right) = \frac{\pi \sigma}{2} (R^4 - r^4)
\)
7. Substituting σ:
- Substitute the value of σ into the equation:
\(
I = \frac{\pi \left( \frac{m}{\pi (R^2 - r^2)} \right)}{2} (R^4 - r^4)
\)
- Simplifying gives:
\(
I = \frac{m (R^4 - r^4)}{2(R^2 - r^2)}
\)
8. Final Simplification:
- Notice that \( R^4 - r^4 = (R^2 + r^2)(R^2 - r^2) \):
\(
I = \frac{m (R^2 + r^2)(R^2 - r^2)}{2(R^2 - r^2)} = \frac{m (R^2 + r^2)}{2}
\)
Final Answer:
The moment of inertia of the disc with a concentric hole about an axis through its center and perpendicular to its plane is:
\(
I = \frac{m}{2} (R^2 + r^2)
\)
- We have a disc of mass m and radius R with a concentric hole of radius r. The moment of inertia (I) we want to calculate is for the entire disc minus the hole.
- Imagine taking a thin ring of thickness dx at a distance x from the center of the disc. The area of this ring can be expressed as:
\(
dA = 2\pi x \, dx
\)
- The mass per unit area (σ) of the disc can be calculated as:
\(
\sigma = \frac{m}{\text{Area of the disc}} = \frac{m}{\pi (R^2 - r^2)}
\)
- The area of the disc is the area of the larger circle minus the area of the hole.
- The mass of the differential ring (dm) can be expressed as:
\(
dm = \sigma \cdot dA = \sigma \cdot 2\pi x \, dx
\)
- The moment of inertia of this ring about the center is given by:
\(
dI = dm \cdot x^2 = \sigma \cdot 2\pi x \, dx \cdot x^2 = 2\pi \sigma x^3 \, dx
\)
- We need to integrate dI from r to R (the limits of the ring):
\(
I = \int_{r}^{R} 2\pi \sigma x^3 \, dx
\)
- Performing the integration:
\(
I = 2\pi \sigma \left( \frac{x^4}{4} \right)_{r}^{R} = 2\pi \sigma \left( \frac{R^4}{4} - \frac{r^4}{4} \right) = \frac{\pi \sigma}{2} (R^4 - r^4)
\)
- Substitute the value of σ into the equation:
\(
I = \frac{\pi \left( \frac{m}{\pi (R^2 - r^2)} \right)}{2} (R^4 - r^4)
\)
- Simplifying gives:
\(
I = \frac{m (R^4 - r^4)}{2(R^2 - r^2)}
\)
- Notice that \( R^4 - r^4 = (R^2 + r^2)(R^2 - r^2) \):
\(
I = \frac{m (R^2 + r^2)(R^2 - r^2)}{2(R^2 - r^2)} = \frac{m (R^2 + r^2)}{2}
\)
The moment of inertia of the disc with a concentric hole about an axis through its center and perpendicular to its plane is:
\(
I = \frac{m}{2} (R^2 + r^2)
\)
Topper's Solved these Questions
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF A PARTICLES & ROTATIONAL MOTIONExercise:SOLVED EXAMPLES
Explore 20 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF A PARTICLES & ROTATIONAL MOTIONExercise:PRACTICE EXERCISE-1
Explore 4 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:7-previous year question
Explore 46 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:IMPECCABLE
Explore 56 Videos
Similar Questions
A disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
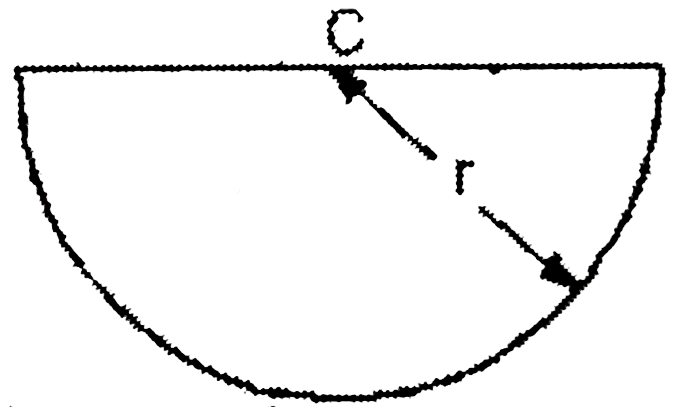
View SolutionA semicircular lamina of mass m and radius r and centre C. Its center of mass is at a distance x from C. Its moment of inertia about an axis through its center of mass and perpendicular to its plane is:
View SolutionSurface mass density of disc of mass m and radius R is Kr2. Then its moment of inertia w.r.t. axis of rotation passing through center and perpendicular to the plane of disc is :
View SolutionA circular disc of radius R and thickness R6 has moment of inertia about an axis passing through its centre and perpendicular to its plane. It is melted and recasted into a solid sphere. The moment of inertia of the sphere about its diameter as axis of rotation is
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionA solid sphere of mass M, radius R and having moment of inertia about as axis passing through the centre of mass as I, is recast into a disc of thickness t, whose moment of inertia about an axis passing through its edge and perpendicular to its plance remains I. Then, radius of the disc will be.
View SolutionIf a circular concentric hole is made on a disc then about an axis passing through the centre of the disc and perpendicular to its plane
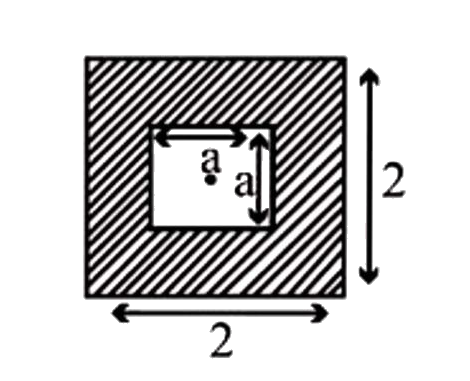
View SolutionA square of a side a is cut from a square of side 2a as shown in the figure. Mass of this square with a hole is M. Then its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane will be
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View Solution