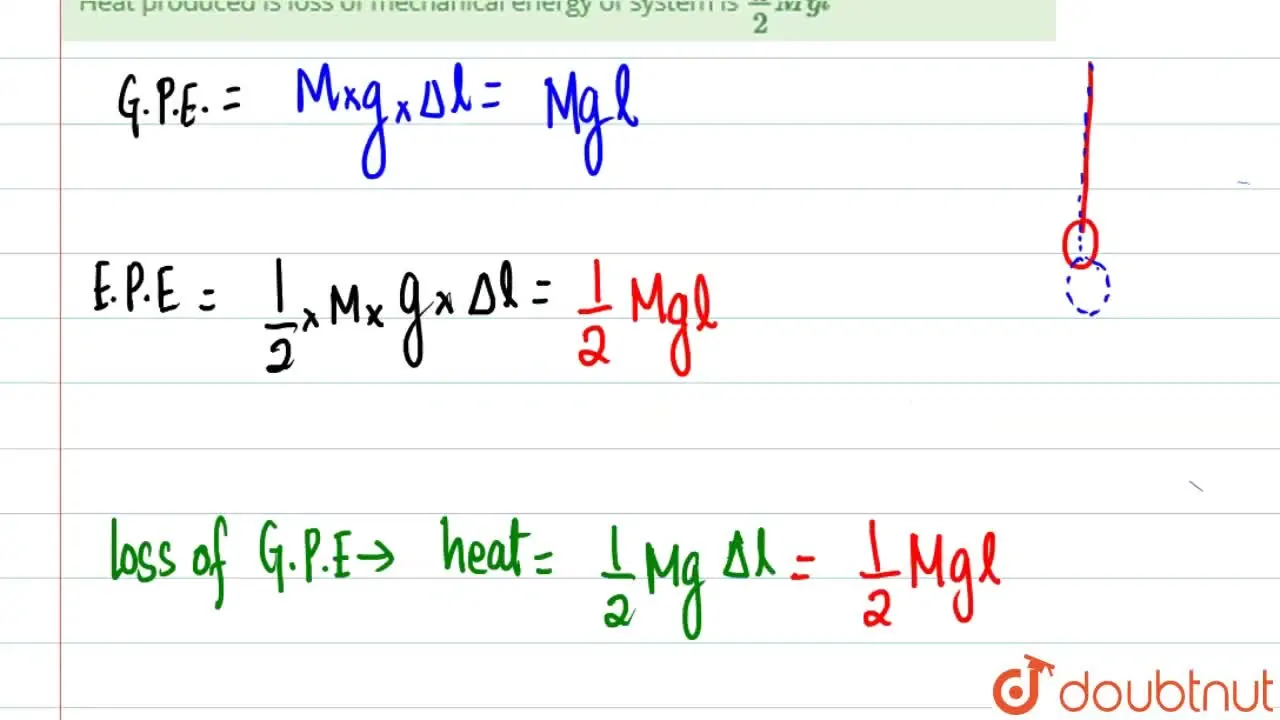A metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
The loss in gravitational potential energy of mass M is Mgl.
The elastic potential energy stored in the wire is Mgl
The elastic potential energy stored in the wire is 12Mgl
Heat produced is loss of mechanical energy of system is 12Mgl
The correct Answer is:A, C, D
Step by step video & image solution for A metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 89 illustration5videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 90 Illustration2videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 887videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A body of mass M is attached to the lower end of a metal wire, whose upper end is fixed . The elongation of the wire is l.
View SolutionA wire of length L, is hanging vertically from a rigid support. If a transverse wave pulse is generated at the free end of wire then which of the following statement is wrong
View SolutionA uniform rope of elngth l and mass m hangs vertically from a rigid support. A block of mass m is attached to the free end of the rope. A transverse pulse of wavelength λ is produced at the lower end of the rope. The wavelength of the pulse, when it reaches the top of the rope. is aλ. Find a2
 View Solution
View SolutionA wire 2 m in length suspended vertically stretches by. 10 mm when mass of 10 kg is attached to the lower end. The elastic potential energy gain by the wire is (take g = 10m/s2)
View SolutionA wire of uniform cross - section is suspended vertically from a fixed point , with a load attached at the lower end . Calculate the fractional change in frequency of the wire due to rise in temperature by t∘C. The coefficient of expansion of the wire is α.
View SolutionA 5m long cylindrical steel wire with radius 2×10−3m is suspended vertically from a rigid support and carries a bob of mass 100kg at the other end . If the bob gets snapped , calculate the change in temperature of the wire ignorning radiation looses. ( Take g=10m/s2)
( For the steel wire , young's modulus =2.1×1011N/m2 , Density =7860kg/m3, Specific heat =420Jkg−∘C ) .View SolutionA wire is suspended vertically from a rigid support. When loaded with a steel weight in air, the wire extends by 16cm. When the weight is completely immersed in Water, the extension is reduced to 14cm. The relative density of the material of the weight is
View SolutionA steel wire is suspended vertically from a rigid support. When loaded with a weight in air, it expands by and when the weight is immersed completely in water, the extension is reduced to Lw. Then relative done of the material of weight is
View SolutionA steel wire is suspended vertically from a rigid support. When loaded with a weight in air, it expands by La and when the weight is immersed completely in water, the extension is reduced to Lw. Then relative density of the material of weight is
View SolutionA uniformly tapering conical wire is made from a material of young's modulus Y and has a normal unextended length L the radii at the upper and lower ends of this conical wire, have values R and 3R, respectively the upper end of the wire is fixed to a rigid support and a mass M is suspended from its lower end. the equilibrium extended length of this wire would equal to:
View Solution