A wire of uniform cross - section is suspended vertically from a fixed point , with a load attached at the lower end . Calculate the fractional change in frequency of the wire due to rise in temperature by t∘C. The coefficient of expansion of the wire is α.
With a temperature change , the tension and mass of the wire will not change but length (I) and linear density (m) will change.
n=12√TMandm=MI
Where M = mass of the wire
∴N=12√TMI=k√I
where k=12√T/M=a(constant)
Differentiating both sides
Δn=k(−12)I−3/2ΔI
∴Δnn(tionalchan≥)=12KI−3/2ΔIKI−1/2
or Δnn=12ΔII=12αt(ΔI=I∝t)
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Subjective
24 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Single Correct
144 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Videos
Similar Questions
A metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
View SolutionA wire 2 m in length suspended vertically stretches by. 10 mm when mass of 10 kg is attached to the lower end. The elastic potential energy gain by the wire is (take g = 10m/s2)
View Solution
Knowledge Check
The adjacent graph shows the extension Δl of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is 106m2 calculate the young's modulus of the material of the wire .
 A2×1011N/m2B2×10−11N/m2C3×10−12N/m2D2x10−13N/m2
A2×1011N/m2B2×10−11N/m2C3×10−12N/m2D2x10−13N/m2Length of wire at room temperature is 4.55 m , when the temperature increases upto 100∘C then its length becomes 4.57 m . The coefficient of linear expansion (α) of the given wire is
A5.021×10−5K−1B6.021×10−5K−1C7.021×10−5K−1D8.021×10−5K−1
A thin rod of negligible mass and area of cross section S is suspended vertically from one end. Length of the rod is L0 at T∘C . A mass m is attached to the lower end of the rod so that when temperature of the rod is reduced to 0∘C its length remains L0 Y is the Young’s modulus of the rod and α is coefficient of linear expansion of rod. Value of m is :
View SolutionA wire suspended vertically from one of itsends is strached by attached a weight of 200N to the lower end . The weight streches the wire by 1mm . Then the elastic energy stored in the wire is
View SolutionThe adjacent graph shows the estension (Δl) of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross-sectional area of the wire is 10−6m2, calculate the Young's modulus of the material of the wire.
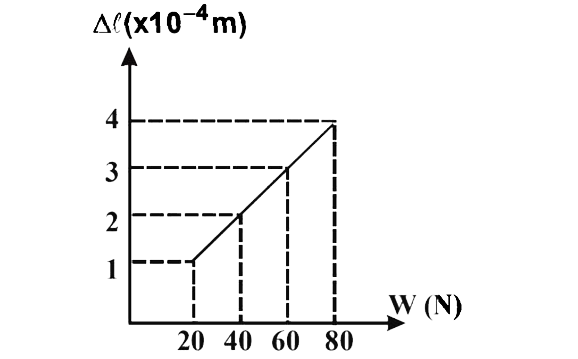
View SolutionEnds of two wires A and B, having resistivityρA=3×105Ωm and ρB=6×10−5ωm of same cross section ara are pointed together to form a single wire. If the resistance of the joined wire does not change with temperature, then find the ratio of their lengths given that temperatue coefficient of resistitivy of wires A and B are α=4×10−5/∘C and α=−4×106/∘C . Assume that mechanical dimensions do not change with temperature.
View SolutionThe adjacent graph shows the extension Δl of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is 106m2 calculate the young's modulus of the material of the wire .

View SolutionA wire 2 mm in diameter is just stretched in between two fixed points at a temperature of 50∘C. Calculate the tension in the wire, when the temperature falls to 30∘C. Coefficient of linear expansion is 11×10−4l∘C and Young modulus is 2.1×1011Nm2
View Solution
