A string of length 25cm is stretched by a load of 10kg. What is the highest overtone that a man of normal hearing capacity can detect ? The mass of the string is
To solve the problem of determining the highest overtone that a man of normal hearing capacity can detect for a string of length 25 cm stretched by a load of 10 kg, we will follow these steps:
Step 1: Determine the Tension in the String
The tension T in the string can be calculated using the formula:
T=mg
where m is the mass (10 kg) and g is the acceleration due to gravity (approximately 9.8m/s2).
Calculating the tension:
T=10kg×9.8m/s2=98N
Step 2: Calculate the Mass per Unit Length (μ)
Since the mass of the string is negligible, we will assume a mass per unit length μ for the string. Given in the video transcript, we have:
μ=0.5×10−3kg/m
Step 3: Calculate the Velocity of the Wave on the String
The velocity v of the wave on the string is given by:
v=√Tμ
Substituting the values we have:
v=√98N0.5×10−3kg/m=√196000≈442.72m/s
Step 4: Determine the Fundamental Frequency
For a string fixed at both ends, the fundamental frequency f1 is given by:
f1=v2L
where L is the length of the string (25 cm = 0.25 m). Thus:
f1=442.72m/s2×0.25m=442.720.5≈885.44Hz
Step 5: Calculate the Frequencies of Overtones
The frequencies of the harmonics (overtones) are given by:
fn=n⋅f1
where n is the harmonic number (1 for fundamental, 2 for first overtone, etc.).
Step 6: Determine the Highest Harmonic Frequency within Human Hearing Range
A person can hear up to 20,000 Hz. To find the highest harmonic n that can be detected:
fn≤20000Hz
Substituting for fn:
n⋅885.44≤20000
Solving for n:
n≤20000885.44≈22.6
Thus, the maximum harmonic n that can be detected is 22.
Step 7: Determine the Highest Overtone
The highest overtone is given by n−1:
Highest overtone=n−1=22−1=21
Final Answer
The highest overtone that a man of normal hearing capacity can detect is 21.
---
The tension T in the string can be calculated using the formula:
T=mg
where m is the mass (10 kg) and g is the acceleration due to gravity (approximately 9.8m/s2).
T=10kg×9.8m/s2=98N
Since the mass of the string is negligible, we will assume a mass per unit length μ for the string. Given in the video transcript, we have:
μ=0.5×10−3kg/m
The velocity v of the wave on the string is given by:
v=√Tμ
Substituting the values we have:
v=√98N0.5×10−3kg/m=√196000≈442.72m/s
For a string fixed at both ends, the fundamental frequency f1 is given by:
f1=v2L
where L is the length of the string (25 cm = 0.25 m). Thus:
f1=442.72m/s2×0.25m=442.720.5≈885.44Hz
The frequencies of the harmonics (overtones) are given by:
fn=n⋅f1
where n is the harmonic number (1 for fundamental, 2 for first overtone, etc.).
A person can hear up to 20,000 Hz. To find the highest harmonic n that can be detected:
fn≤20000Hz
Substituting for fn:
n⋅885.44≤20000
Solving for n:
n≤20000885.44≈22.6
Thus, the maximum harmonic n that can be detected is 22.
The highest overtone is given by n−1:
Highest overtone=n−1=22−1=21
The highest overtone that a man of normal hearing capacity can detect is 21.
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Subjective
24 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Single Correct
144 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Videos
Similar Questions
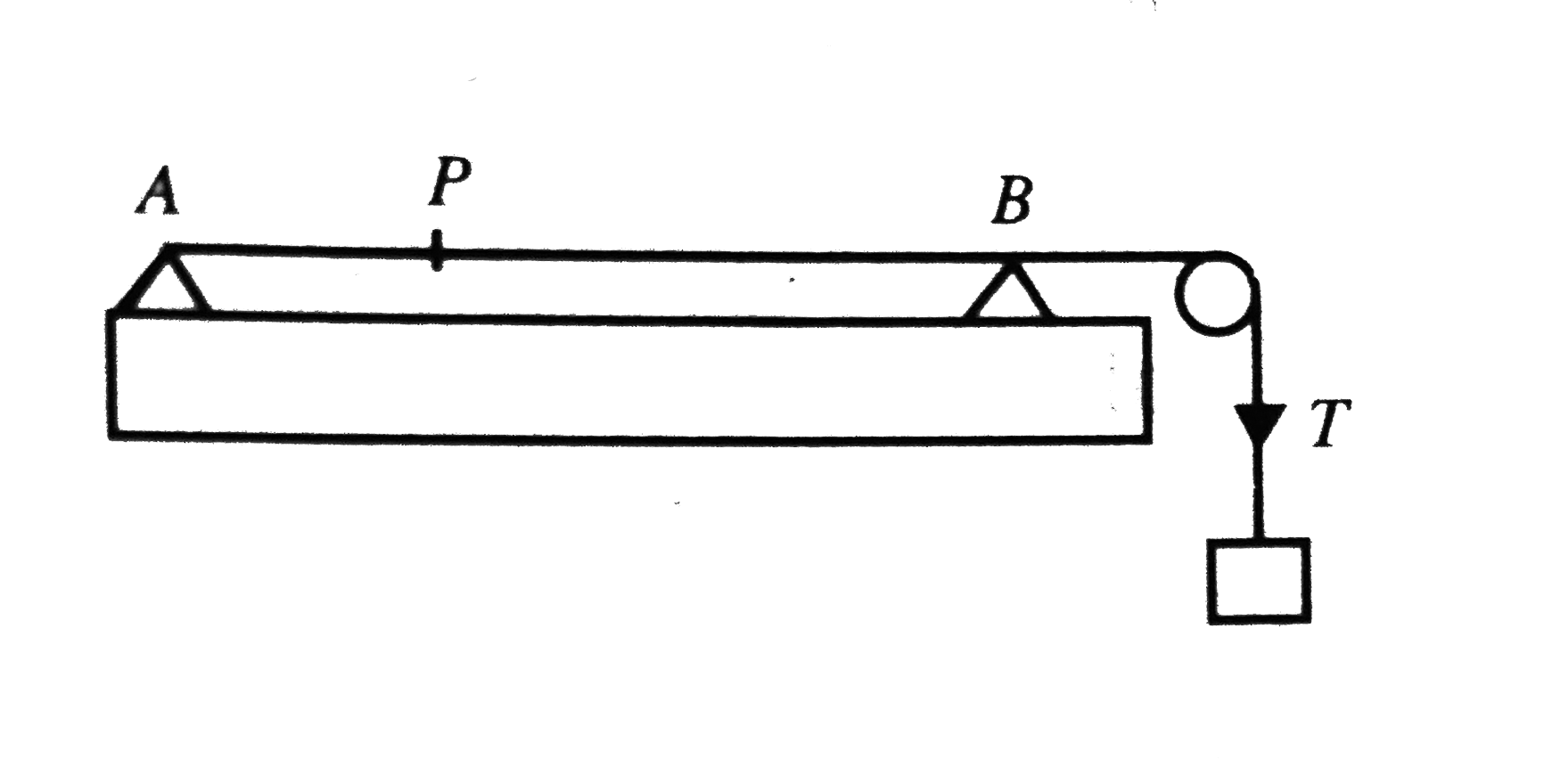
A sonometer strings AB of length 1m is stretched by a load and the tension T is adjusted so that the string resonates to a frequency of 1kHz. Any point P of the wire may be held fixed by use of a movable bridge that can slide along the base of sonometer.
View SolutionA particle of mass 1kg is attached to a string of length 5m. The string is attached to a fixed point O. It is released from theposition as shown in Fig. Calculate
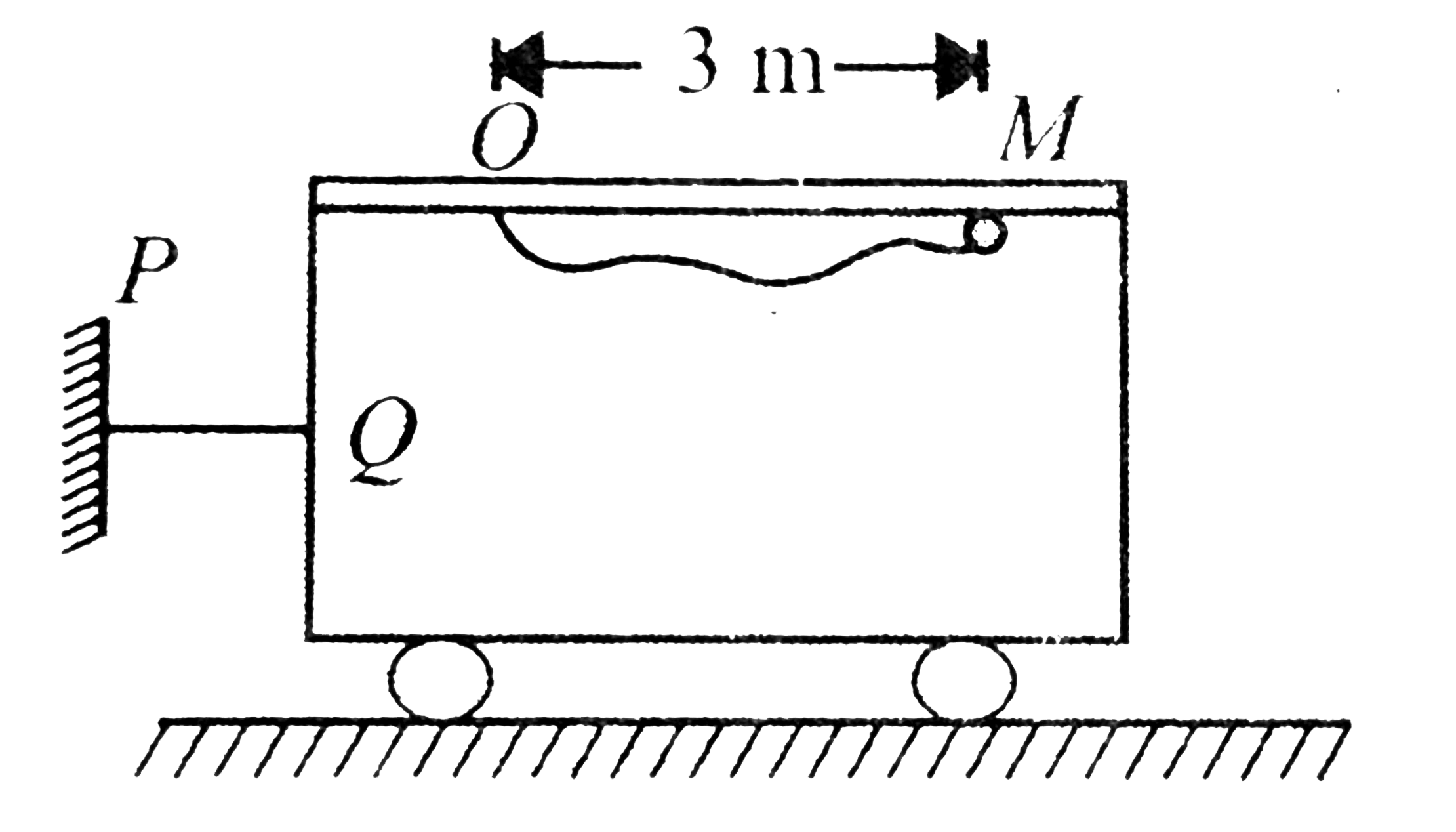
a. the impulse developed in the string when it becorries taut,
b. the velocity of the particle just after the string becomes taut,
c. the impulse developed in this string PQ at this instant.
View Solution
Knowledge Check
A stone of mass 5 kg is tied to a string of length 10 m is whirled round in a horizontal circle. What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N?
A10ms−1B15ms−1C20ms−1D25ms−1
A 60.0 cm guitar string under a tension of 50.0 N has a mass per unit length of 0.100 g/cm. What is the highest resonance frequency of the string that can be heard by a person able to hear frequencies upto 20000 Hz?
View SolutionA string of 7 m length has a mass of 0.035 kg. If tension in the string is 60.5 N, then speed of a wave on the string is :
View SolutionA string of length 2m and mass 2 gmn is stretched by a certain tension so that it vibrates in 4 segments with a frequency of 600 Hz. What is the tension ?
View SolutionA transverse sine wave of amplitude 10 cm and wavelength 200 cm travels from left to right along a long horizontal stretched, string with a speed of 100 cm/s. Take the origin at left end of the string. At time t = 0 the left end of the string is at the origin and is moving downward. Then the equation of the wave will be ( in CGS system )
View SolutionA string of 7m length has a mass of 0.035kg. If tension in the string is 60.N, then speed of a wave on the string is
View SolutionThe frequency of the fourth harmonic in a stretched string of length 20 cm is 500 Hz. (i) Calculate the velocity of the wave in the string? (ii) For what value of tension, will the velocity in the string be 100 ms−1?
View SolutionAn elastic string has a force constant k and mass m. the string hangs vertically, and a block of an unknown mass is attached to its bottom end. It is known that the mass of the blocks is much greater than that of the string. The hanging block stretches the string to twice its relaxed length. how long (t) would it t take for a low-amplitude transwerse pulse to travel the length of the string stretched by the hanging block ? m=1 kg, k=12N/m.
View Solution
