A string fixed at both ends is vibrating in the lowest possible mode of vibration for which a point at quarter of its length from one end is a point of maximum displacement. The frequency of vibration in this mode is 100 Hz. What will be the frequency emitted when it vibrates in the next mode such that this point of maximum displacement?
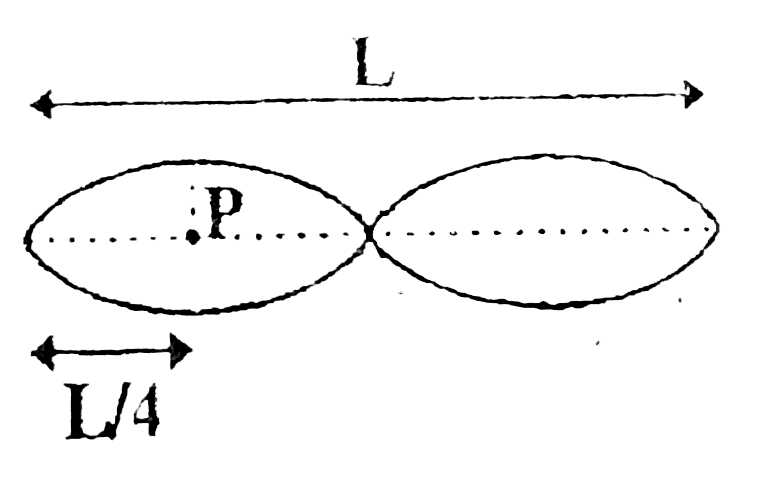
Since the mode has an antinode at 1/4 point
I/4=λ/4orI=λand100=cT (c=nλ)
In the next mode , between the nearest end 1/4 point from this end , there must appear one node and antinode.
∴I/4=3λ'4whereλ' is the wavelength of the next mode
⇒λ'=I/3
∴n'=cI/3=3cI=3×100=300Hz
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Subjective24videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Single Correct144videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type5videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 241videos
THERMODYNAMICS
Similar Questions
A string fixed at both ends is vibrating in the lowest mode of vibration for which a point at quarter of its length from one end is a point of maximum vibration . The note emitted has a frequency of 100Hz. What will be the frequency emitted when it vibrates in the next mode such that this point is again a point of maximum vibratin ?
View SolutionA string fixed at both ends is vibrating such that a point at quarter of its length from one end is a point of maximum displacement. The frequency of vibration in this mode is 100Hz. If the frequency emitted when it vibrates in the next mode such that this point is again a point of maximum displacement is 100k then find the value of k.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
When a string fixed at its both ends vibrates in 1 loop, 2 loops, 3 loops and 4 loops, the frequencies are in the ratio
A1 : 1 : 1 : 1B1 : 2 : 3 : 4C4 : 3 : 2 : 1D1 : 4 : 9 : 16 - Question 2 - Select One
A string fixed at its both ends vibrates in 5 loops as shown in the figure. The total number of nodes and antinodes are respectively
 A5,6B6,5C7,4D4,7
A5,6B6,5C7,4D4,7
A string fixed at both is vibrating in the lowest mode of vibration for which a point at quarter of its length from one end is a point of maximum displacement . The frequency of vibration emitted when it vibrates in the next mode such that this point is again a point of maximum displacement ?
View SolutionA string fixed at both ends, is vibrating in a particular mode of vibration. Vibration is such that a point on string is at maximum displacement and it is at a distance of one fourth of length of string from one end. The frequency of vibration in thus mode is 200Hz. What will be the frequency of vibration when it vibrates in next mode such that the same point is at maximum displacement?
View SolutionA string of length 'L' is fixed at both ends . It is vibrating in its 3rd overtone with maximum amplitude 'a'. The amplitude at a distance L/3 from one end is
View SolutionThe maximum displacement of a vibrating object in a medium from its mean position
View SolutionA string of length l is fixed at both ends and is vibrating in second harmonic. The amplitude at anti-node is 5 mm. The amplitude of a particle at distance l/8 from the fixed end is
View SolutionAn open organ pipe of length L vibrates in its fundamental mode. The pressure variation is maximum
View Solution
