A string fixed at both ends is vibrating such that a point at quarter of its length from one end is a point of maximum displacement. The frequency of vibration in this mode is 100Hz. If the frequency emitted when it vibrates in the next mode such that this point is again a point of maximum displacement is 100k then find the value of k.
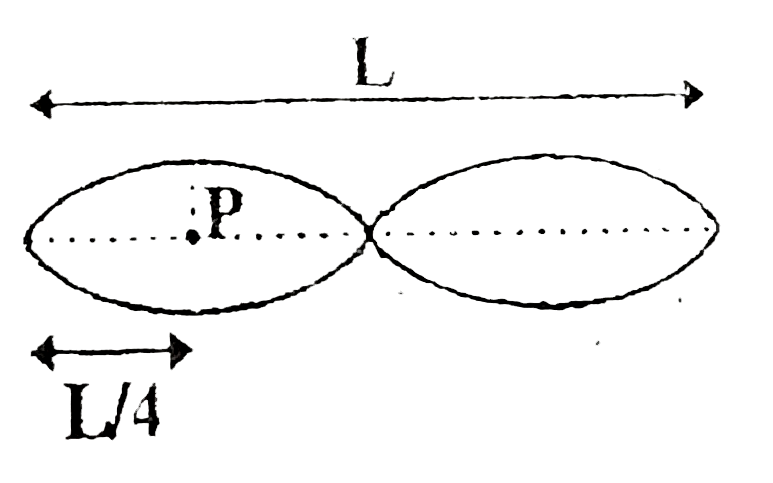
The figure rerpesents the mode of vibration for which frequency is 100Hz.
Here, L=λ
In the next higher mode with P again an anti-node, for every L/4 length, there will be one extra loop. Thus for the total string, total number of loops =6
⇒ Desired frequency =(6/2)100Hz=300Hz

Similar Questions
A string fixed at both is vibrating in the lowest mode of vibration for which a point at quarter of its length from one end is a point of maximum displacement . The frequency of vibration emitted when it vibrates in the next mode such that this point is again a point of maximum displacement ?
View SolutionA string fixed at both ends is vibrating in the lowest mode of vibration for which a point at quarter of its length from one end is a point of maximum vibration . The note emitted has a frequency of 100Hz. What will be the frequency emitted when it vibrates in the next mode such that this point is again a point of maximum vibratin ?
View Solution
Knowledge Check
When a string fixed at its both ends vibrates in 1 loop, 2 loops, 3 loops and 4 loops, the frequencies are in the ratio
A1 : 1 : 1 : 1B1 : 2 : 3 : 4C4 : 3 : 2 : 1D1 : 4 : 9 : 16
A string fixed at both ends, is vibrating in a particular mode of vibration. Vibration is such that a point on string is at maximum displacement and it is at a distance of one fourth of length of string from one end. The frequency of vibration in thus mode is 200Hz. What will be the frequency of vibration when it vibrates in next mode such that the same point is at maximum displacement?
View SolutionThe string in E sonometer is touched lightly at a point one-third of its length from one end. Which harmonics is produced ?
View SolutionThe velocity of waves in a string fixed at both ends is 2 m / s . The string forms standing waves with nodes 5.0 cm apart. The frequency of vibration of the string in Hz is
View SolutionA blade, fixed at one end, is made to vibrate by pressing its other end and then releasing it. State one way in which the frequency of vibrations of the blade can be lowered.
View SolutionIn a sinusoidal wave the time required for a particular point to move from equilibrium position to maximum displacement is 0.17s, then the frequency of wave is:
View SolutionA string, fixed at both ends, vibrates in a resonant mode with a separation of 2.0 cm between the consecutive nodes. For the next higher resonant frequency, this separation is reduced to 1.6 cm. Find the length of the string.
View SolutionA wire of length 2.00 m is stretched to a tension of 160 N. If the fundamental frequency of vibration is 100 Hz, find its linear mass density.
View Solution

