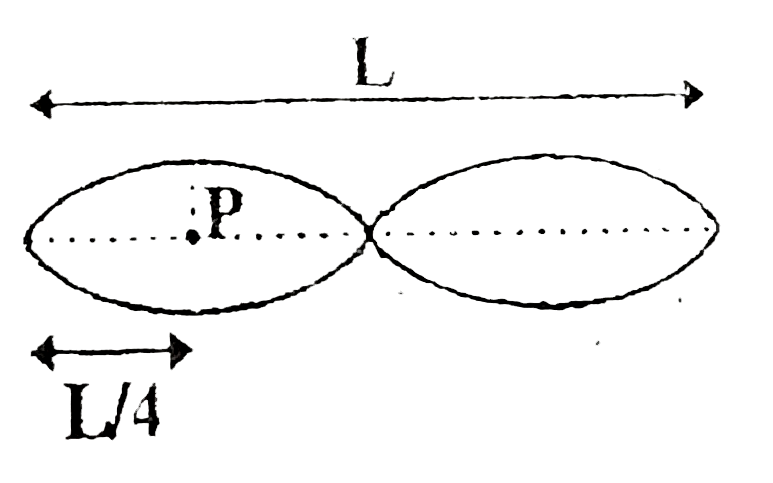
A string fixed at both ends is vibrating in the lowest mode of vibration for which a point at quarter of its length from one end is a point of maximum vibration . The note emitted has a frequency of $100 H z$ . What will be the frequency emitted when it vibrates in the next mode such that this point is again a point of maximum vibrating ?

Video Solution

Text Solution

Verified by Experts

Since the mode has an antinode at $1 / 4$ point
$I / 4 = λ / 4 or I = λ and 100 = \frac{c}{T}$ $(c = n λ)$
In the next mode , between the nearest end $1 / 4$ point from this end , there must appear one node and antinode.
$∴ I / 4 = \frac{3 λ'}{4} w h e r e λ'$ is the wavelength of the next mode
$\Rightarrow λ' = I / 3$
$∴ n' = \frac{c}{I / 3} = \frac{3 c}{I} = 3 \times 100 = 300 H z$

Updated on:21/07/2023

A string fixed at both is vibrating in the lowest mode of vibration for which a point at quarter of its length from one end is a point of maximum displacement . The frequency of vibration emitted when it vibrates in the next mode such that this point is again a point of maximum displacement ?
A400 Hz
B200 Hz
C600 Hz
D300 hz
A string fixed at its both ends vibrates in 5 loops as shown in the figure. The number of nodes and antinodes respectively

A5,6
B6,5
C7,4
D4,7
A string of length l is fixed at both ends. It is vibrating in its $3^{r d}$ overtone with maximum amplitude 'a'. The amplitude at a distance l/3 from one end is
Aa
B0
C $\frac{\sqrt{3 a}}{2}$
D $\frac{a}{2}$