A copper wire of negligible mass, length l and corss-section A is kept on a smooth horizontal table with one end fixed. A ball of mass m is attached to the other end. The wire and the ball are rotating with an angular velocity ω. If elongation in the wire is Δl, obtain the expression for the Young's modulus.
mL2ωAΔL
mω2L2AΔL
mω2LAΔL
mωLAΔL
mL2ωAΔL
mω2L2AΔL
mω2LAΔL
mωLAΔL
The correct Answer is:B
To derive the expression for Young's modulus for the given scenario, we will follow these steps:
Step 1: Identify the forces acting on the ball
The ball of mass m is rotating in a circular path with radius L. The centripetal force required to keep the ball in circular motion is given by:
Fc=mω2L
where ω is the angular velocity.
Step 2: Relate the tension in the wire to the centripetal force
The tension T in the wire must provide the necessary centripetal force to keep the ball moving in a circle. Therefore, we can write:
T=Fc=mω2L
Step 3: Define stress and strain
Young's modulus Y is defined as the ratio of stress to strain.
- Stress is given by:
Stress=TA
where A is the cross-sectional area of the wire.
- Strain is defined as:
Strain=ΔLL
where ΔL is the elongation of the wire and L is the original length of the wire.
Step 4: Substitute the expressions for stress and strain into the Young's modulus formula
Using the definitions of stress and strain, we can write Young's modulus as:
Y=StressStrain=TAΔLL=T⋅LA⋅ΔL
Step 5: Substitute the expression for tension into the Young's modulus formula
Now, we substitute T=mω2L into the Young's modulus equation:
Y=(mω2L)⋅LA⋅ΔL
This simplifies to:
Y=mω2L2AΔL
Conclusion
Thus, the expression for Young's modulus Y is:
Y=mω2L2AΔL
Final Answer
The correct option is:
mω2L2AΔL
---
The ball of mass m is rotating in a circular path with radius L. The centripetal force required to keep the ball in circular motion is given by:
Fc=mω2L
where ω is the angular velocity.
The tension T in the wire must provide the necessary centripetal force to keep the ball moving in a circle. Therefore, we can write:
T=Fc=mω2L
Young's modulus Y is defined as the ratio of stress to strain.
Stress=TA
where A is the cross-sectional area of the wire.
Strain=ΔLL
where ΔL is the elongation of the wire and L is the original length of the wire.
Using the definitions of stress and strain, we can write Young's modulus as:
Y=StressStrain=TAΔLL=T⋅LA⋅ΔL
Now, we substitute T=mω2L into the Young's modulus equation:
Y=(mω2L)⋅LA⋅ΔL
This simplifies to:
Y=mω2L2AΔL
Thus, the expression for Young's modulus Y is:
Y=mω2L2AΔL
The correct option is:
mω2L2AΔL
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assignment (SECTION - C)
Explore 2 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assignment (SECTION - D)
Explore 3 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assignment (SECTION - A)
Explore 31 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:SECTION - J
Explore 9 Videos
- Mock test 03Book:AAKASH INSTITUTE ENGLISHChapter:Mock test 03Exercise:EXAMPLE
Explore 44 Videos
Similar Questions
A copper wire of negligible mass, 1m length and cross-sectional area 10−6m2 is kept on a smooth horizontal table with one end fixed. A ball of mass 1kg is attached to the other end. The wire and the ball are rotating with an angular velocity of 20rad/s. If the elongation in the wire is 10−3m.
a. Find the Young's modulus of the wire (in terms of ×1011N/m2).
b. If for the same wire as stated above, the angular velocity is increased to 100rad/s and the wire breaks down, find the breaking stress (in terms of ×1010N/m2).
View SolutionA body of mass M is attached to the lower end of a metal wire, whose upper end is fixed . The elongation of the wire is l.
View SolutionA uniform rod of mass m and length L is kept on a horizontal table with L4 length on the table as shown in figure. As the string attached to the end B is cut, the angular acceleration of the rod about point C will be
_PHY_E05_242_Q01.png)
View SolutionA uniform rod of length l, mass m, cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity ω. Find the total extension in the rod due to the tension produced in the rod.
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
View SolutionA copper rod of length l is rotated about one end perpendicular to the magnetic field B with constant angular velocity ω . The induced e.m.f between the two ends is
View Solution
A rod of mass 2 kg ad length 2 m is rotating about its one end O with an angular velocity ω=4rad/s. Find angular momentum of the rod about the axis rotation.
View SolutionA particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity ω in gravity free space. The increase in length of the spring is
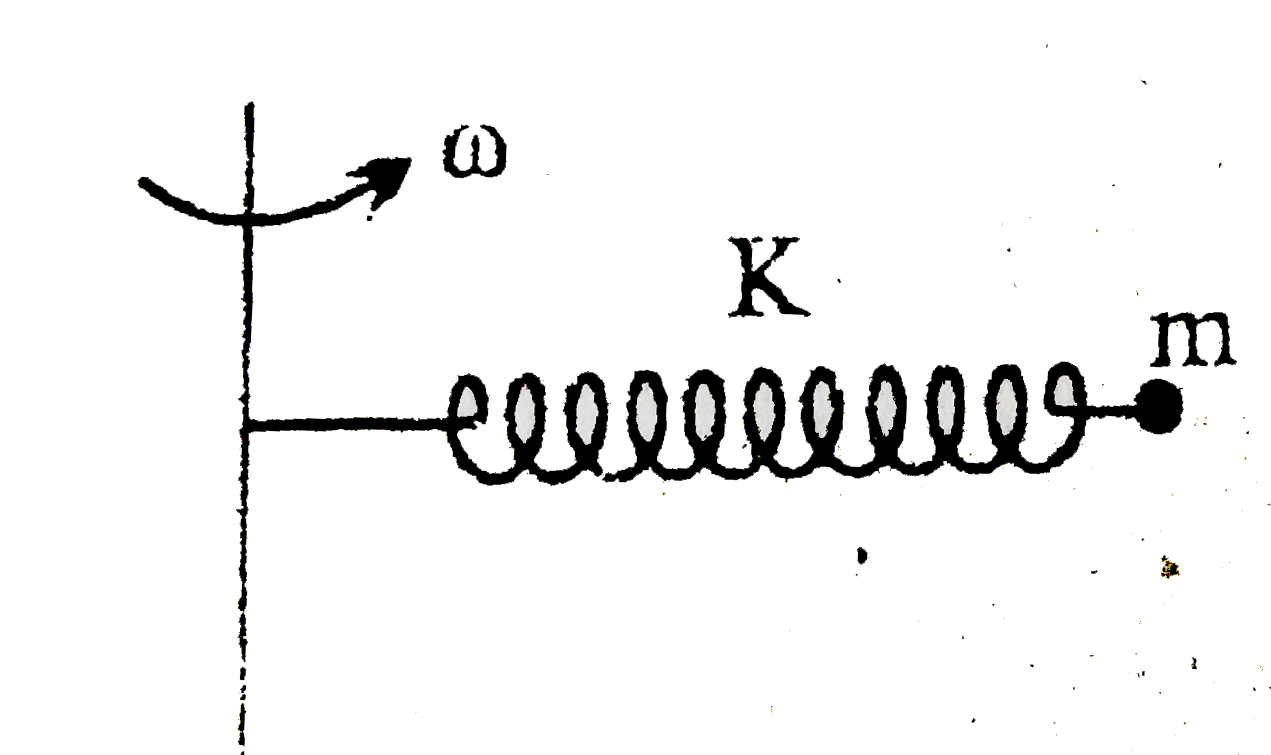
View Solution

