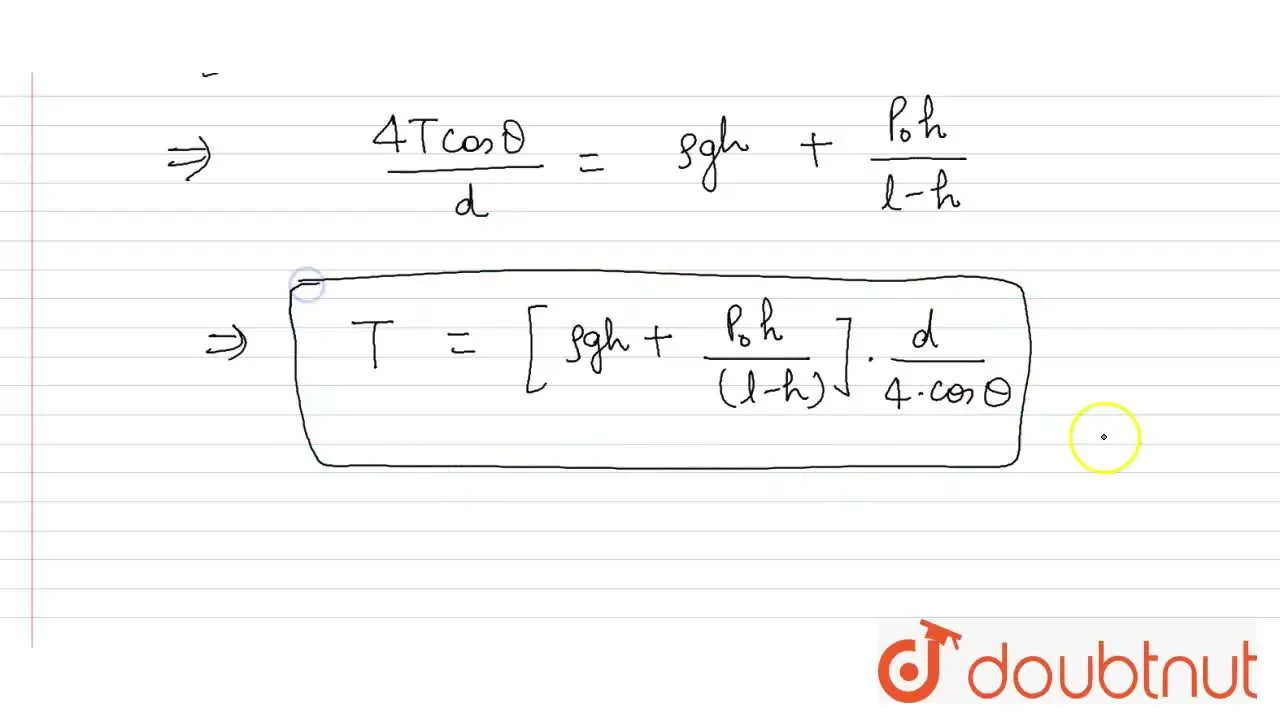
When a vertical capillary of length with the sealed upper end was brought in contact with the surface of a liquid, the level of this liquid rose to the height h. The liquid density is ρ, the inside diameter the capillary is d, the contact angle is θ, the atmospheric pressure is ρ0. Find the surface tension of the liquid. (Temperature this process remains constant.)

The correct Answer is:P04cosθ
Applying Boyle's law
p0Al=[(P0−hρg)+4Tdcosθ]a(L−h)
T=P04cosθ[(hL−h)+hρg]d
Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Single Correct112videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Multiple Correct17videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.39videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
Similar Questions
When a vertical capillary of length l with a sealed upper end was brought in contact with the surface of a liquid, the level of this liquid rose to the height h. The liquid density is ρ, the inside diameter the capillary is d, the contact angle is θ, the atmospheric pressure is ρ0. Find the surface tension of the liquid. (Temperature in this process remains constant.)
 View Solution
View SolutionThe pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
View SolutionA vertical capillary is brought in contact with the water surface (surface tension = T). The radius of the capillary is r and the contact angle θ=0∘. The increase in potential energy of the water (density =ρ) is
View SolutionA liquid is filled in a spherical container of radius R up to a height h. At this position the liquid surface at the end is also horizontal. The contact angle is
 View Solution
View SolutionA liquid of density 'ρ' is rotated with an angular speed 'ω' as shown in figure. Using the pressure equation concept find the equation of free surface of the liquid.
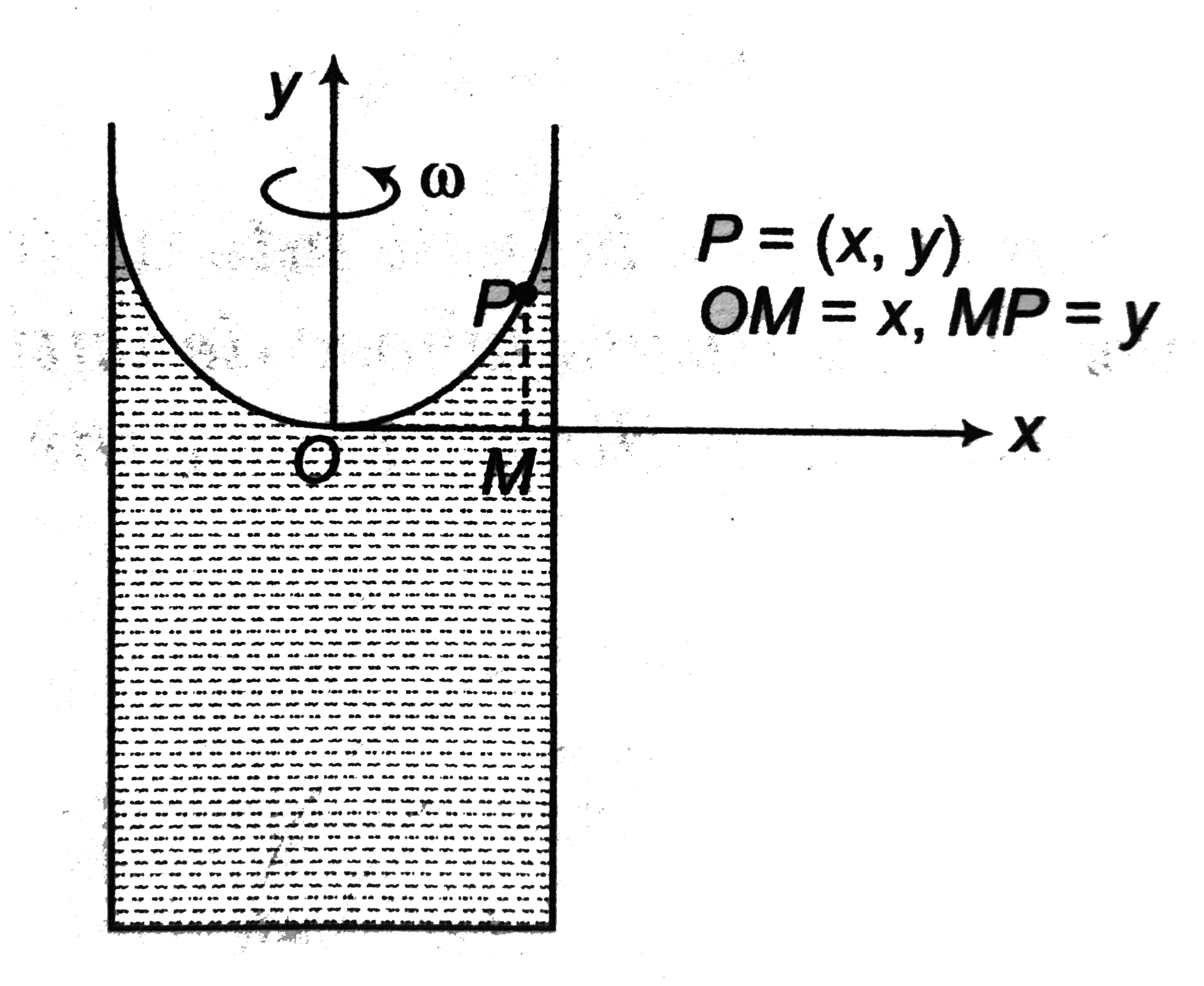 .View Solution
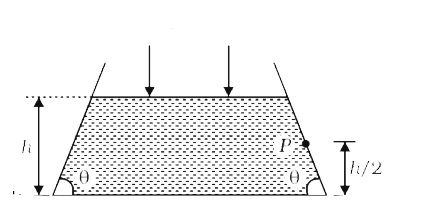
.View SolutionA container (see figure) contains a liquid upto a height h. The density of the liquid is The gauge pressure at point P is ρghx. Find the value of x
 View Solution
View SolutionA liquid of density ρ and surface tension σ rises in a capillary tube of diameter d. Angle of contact between the tube and liquid is zero. The weight of the liquid in the capillary tube is:
View SolutionTwo vertical plates submerged partially in a wetting liquid form a wedge with a very small angle δφ. The edge of this wedge is vertical. The density of the liquid is ρ, its surface tension is α, the contact angle is θ. Find the height h, to which the liquid rises, as a function of the distance x from the edge.
View SolutionA long glass capillary (radius R) is taken out of liquid (surface tension S and density ρ) in vertical position. Angle of contact everywhere is zero. Atmospheric pressure is P0. It is observed that the capillary retains some liquid.
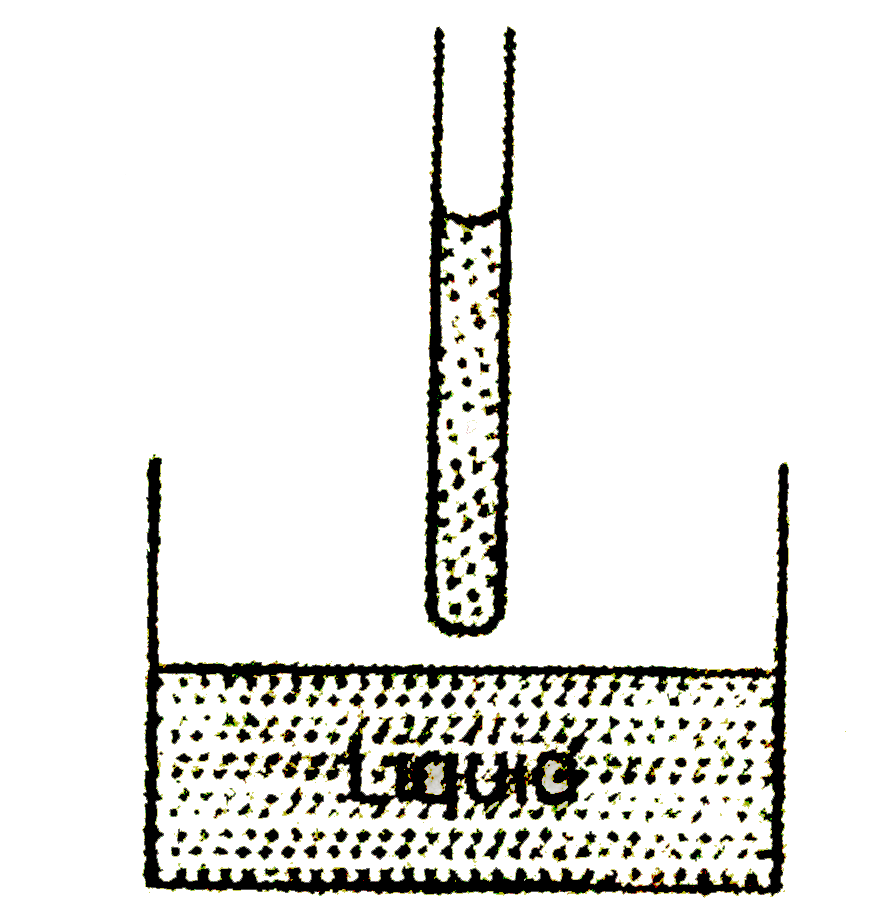
The length of liquid column retained in the capillary isView SolutionA long glass capillary (radius R) is taken out of liquid (surface tension S and density ρ) in vertical position. Angle of contact everywhere is zero. Atmospheric pressure is P0. It is observed that the capillary retains some liquid.
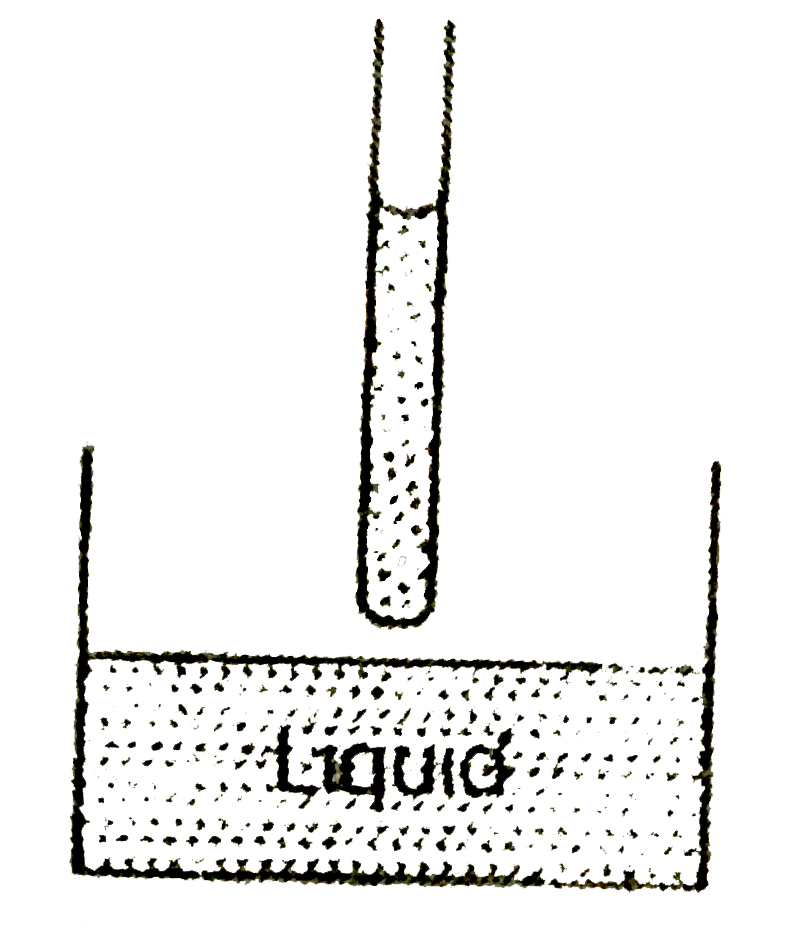
The radius of curvature of meniscus at the bottom of tube isView Solution