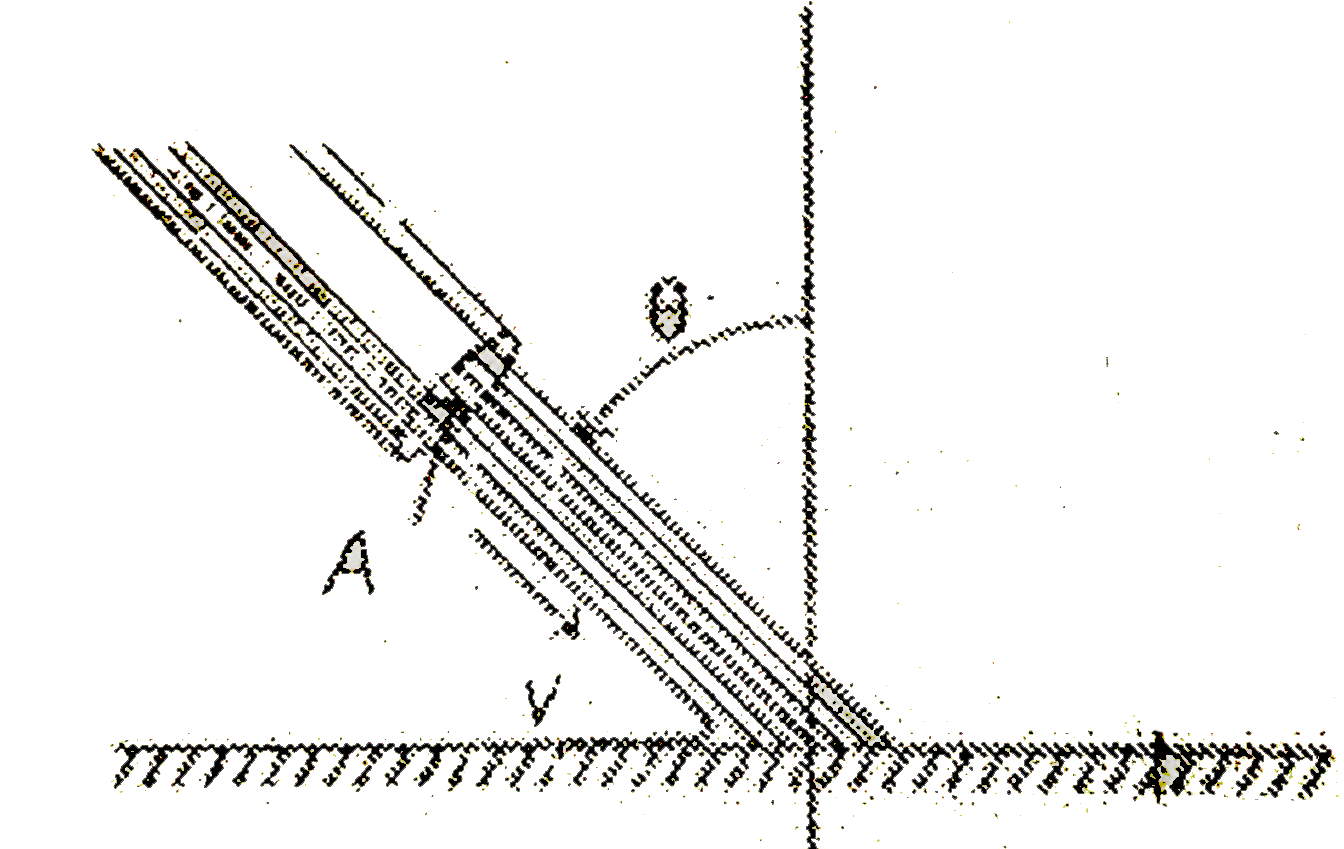
Two vertical plates submerged partially in a wetting liquid form a wedge with a very small angle δφ. The edge of this wedge is vertical. The density of the liquid is ρ, its surface tension is α, the contact angle is θ. Find the height h, to which the liquid rises, as a function of the distance x from the edge.
2Tρgx(δθ)
2Tρgx
2T(δθ)ρgx
Tρgx(δθ)
To solve the problem of finding the height h to which the liquid rises as a function of the distance x from the edge of the wedge formed by two vertical plates submerged in a wetting liquid, we can follow these steps:
1. Understand the Geometry:
- We have two vertical plates forming a wedge with a very small angle δφ.
- The liquid will rise to a height h due to the effects of surface tension and gravity.
2. Identify the Forces:
- The height h creates a hydrostatic pressure due to the liquid column above it, which can be expressed as:
Pressure due to liquid=ρgh
- The surface tension acts along the edge of the liquid surface, contributing to the rise of the liquid.
3. Set Up the Energy Balance:
- The energy associated with the liquid column can be expressed as:
Energy due to liquid=ρgh⋅Area=ρgh⋅12h⋅dx
- The energy due to surface tension can be expressed as:
Energy due to surface tension=2⋅α⋅cos(θ)⋅h⋅dx
4. Write the Energy Equation:
- The total energy balance can be written as:
ρgh2⋅dx2−2αcos(θ)h⋅dx=0
5. Factor Out Common Terms:
- Taking dx and other common terms out, we have:
ρg2h2−2αcos(θ)h=0
6. Rearranging the Equation:
- Rearranging gives:
ρg2h2=2αcos(θ)h
- Dividing both sides by h (assuming h≠0):
ρg2h=2αcos(θ)
7. Solve for Height h:
- Solving for h gives:
h=4αcos(θ)ρg⋅δφ⋅x
8. Final Expression:
- Thus, the height h to which the liquid rises as a function of the distance x from the edge is:
h=2αcos(θ)ρgδφx
- We have two vertical plates forming a wedge with a very small angle δφ.
- The liquid will rise to a height h due to the effects of surface tension and gravity.
- The height h creates a hydrostatic pressure due to the liquid column above it, which can be expressed as:
Pressure due to liquid=ρgh
- The surface tension acts along the edge of the liquid surface, contributing to the rise of the liquid.
- The energy associated with the liquid column can be expressed as:
Energy due to liquid=ρgh⋅Area=ρgh⋅12h⋅dx
- The energy due to surface tension can be expressed as:
Energy due to surface tension=2⋅α⋅cos(θ)⋅h⋅dx
- The total energy balance can be written as:
ρgh2⋅dx2−2αcos(θ)h⋅dx=0
- Taking dx and other common terms out, we have:
ρg2h2−2αcos(θ)h=0
- Rearranging gives:
ρg2h2=2αcos(θ)h
- Dividing both sides by h (assuming h≠0):
ρg2h=2αcos(θ)
- Solving for h gives:
h=4αcos(θ)ρg⋅δφ⋅x
- Thus, the height h to which the liquid rises as a function of the distance x from the edge is:
h=2αcos(θ)ρgδφx
Similar Questions
When a vertical capillary of length l with a sealed upper end was brought in contact with the surface of a liquid, the level of this liquid rose to the height h. The liquid density is ρ, the inside diameter the capillary is d, the contact angle is θ, the atmospheric pressure is ρ0. Find the surface tension of the liquid. (Temperature in this process remains constant.)

View SolutionWhen a vertical capillary of length with the sealed upper end was brought in contact with the surface of a liquid, the level of this liquid rose to the height h. The liquid density is ρ, the inside diameter the capillary is d, the contact angle is θ, the atmospheric pressure is ρ0. Find the surface tension of the liquid. (Temperature this process remains constant.)

View SolutionTwo parallel glass plates are dipped partly in the liquid of density 'd' keeping them vertical. If the distance between the plates is 'x', Surface tension is T and angle of contact is θ then rise of liquid between the plates due to capillary will be
View SolutionA liquid is coming out from a vertical tube. The relation between the weight of the drop W , surface tension of the liquid T and radius of the tube r is given by, if the angle of contact is zero
View SolutionFind value of surface tension if contact angle is 0 and after lowering tube height of liquid is 15 cm and radius is 0.015 cm (density = 900 kg/(m3)) (g = 10 m/(s2)
View SolutionA capillary tube with inner cross-section in the form of a square of side a is dipped vertically in a liquid of density ρ and surface tension ρ which wet the surface of capillary tube with angle of contact θ . The approximate height to which liquid will be raised in the tube is : (Neglect the effect of surface tension at the corners of capillary tube)
View SolutionA liquid of density ρ and surface tension σ rises in a capillary tube of diameter d. Angle of contact between the tube and liquid is zero. The weight of the liquid in the capillary tube is:
View SolutionA stream of liquid, set at an angle θ, is directed against a plane surface (figure). The liquid, after hitting the surface, spreads over it. Find the pressure on the surface. The density of the liquid is ρ and its velocity is v.
View SolutionA student writes the equation for the capillary rise of a liquid in a tube as h=ρg2Tcosθ, where r is the radius of the capillary tube, ρ is the density of liquid, T is the surface tension and θ is the angle of contact. Check the correctness of the equation using dimensional analysis?
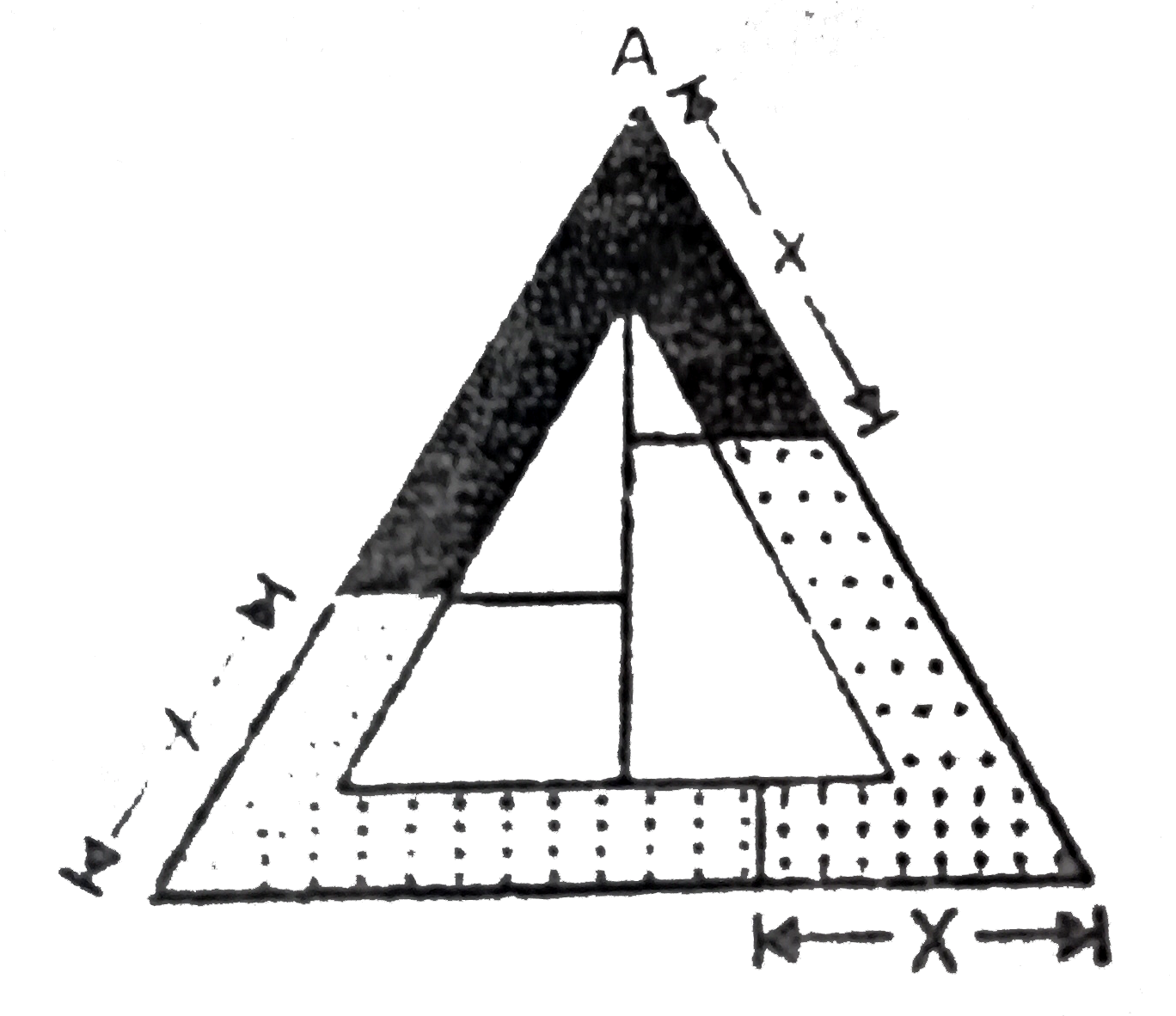
View SolutionA closed tube in the form of an equilateral triangle of side l contains equal volumes of three liquids which do not mix and is placed vertically with its lowest side horizonta. Find 'x' in the figure if the densities of the liquids are in A.P.
View Solution
