What is the height to which a liquid rises between two long parallel plates, at d distance a part between them T and p are surface tension and density of liquid respectively and contact angle between plate and liquid is zero.
4Tpgd
2Tpgd
Tpgd
T2pgd
The correct Answer is:A
To find the height to which a liquid rises between two long parallel plates, we can use the principles of capillarity. The height h of the liquid column can be derived from the balance of forces acting on the liquid.
1. Understand the Forces Involved:
- The liquid will rise due to the surface tension T acting on the liquid's surface.
- The force due to surface tension can be expressed as F=2T⋅L, where L is the length of the liquid column in contact with the plates.
2. Balance the Forces:
- The upward force due to surface tension must balance the downward gravitational force acting on the liquid column.
- The gravitational force can be expressed as Fg=m⋅g=ρ⋅V⋅g, where V is the volume of the liquid column, ρ is the density of the liquid, and g is the acceleration due to gravity.
3. Express the Volume:
- The volume V of the liquid column can be expressed as V=A⋅h, where A is the cross-sectional area of the liquid column and h is the height of the liquid column.
- For a narrow gap between the plates, A can be approximated as L⋅d, where d is the distance between the plates.
4. Set Up the Equation:
- The upward force due to surface tension is equal to the downward gravitational force:
2T⋅L=ρ⋅(L⋅d⋅h)⋅g
5. Simplify the Equation:
- Cancel L from both sides (assuming L≠0):
2T=ρ⋅d⋅h⋅g
6. Solve for Height h:
- Rearranging the equation gives:
h=2Tρ⋅g⋅d
Final Answer:
The height to which the liquid rises between the two plates is:
h=2Tρgd
- The liquid will rise due to the surface tension T acting on the liquid's surface.
- The force due to surface tension can be expressed as F=2T⋅L, where L is the length of the liquid column in contact with the plates.
- The upward force due to surface tension must balance the downward gravitational force acting on the liquid column.
- The gravitational force can be expressed as Fg=m⋅g=ρ⋅V⋅g, where V is the volume of the liquid column, ρ is the density of the liquid, and g is the acceleration due to gravity.
- The volume V of the liquid column can be expressed as V=A⋅h, where A is the cross-sectional area of the liquid column and h is the height of the liquid column.
- For a narrow gap between the plates, A can be approximated as L⋅d, where d is the distance between the plates.
- The upward force due to surface tension is equal to the downward gravitational force:
2T⋅L=ρ⋅(L⋅d⋅h)⋅g
- Cancel L from both sides (assuming L≠0):
2T=ρ⋅d⋅h⋅g
- Rearranging the equation gives:
h=2Tρ⋅g⋅d
The height to which the liquid rises between the two plates is:
h=2Tρgd
Topper's Solved these Questions
Similar Questions
Knowledge Check
What is the height to which a liquid rises between two long parallel plates, a distance d apart ? (Surface tension of liquid is T and density is ρ)
A4TρgdB2TρgdCTρgdDT2ρgd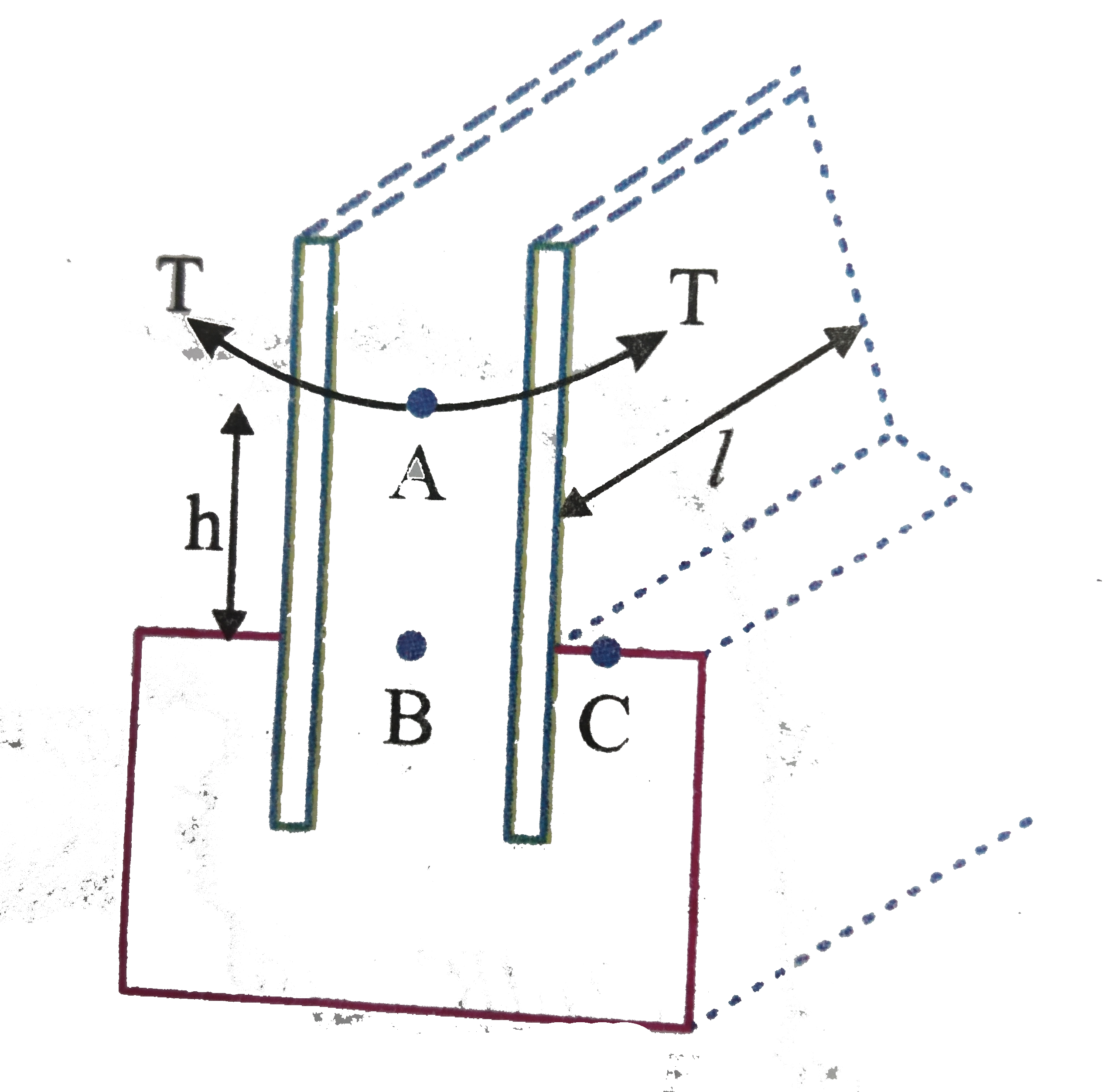
Expression for the height of capillary rise between two parallel plates dipping liquid of density σ separated by a distance d. The surface tension of the liquid is T. [Take angle of contact to be zero]Ah=2TσdgBh=2dσTCh=σTdDh=2T2σdTwo parallel glass plates separated by a small distance x are dipped partly in a liquid of density " d" keeping them vertical .The surface tension of the liquid is T and angle of contact is θ . What is the rise of the liquid between the plates due to capillarity ?
ATcosθxdB2TcosθxdgC2TxdgcosθDTcosθxdg
The height to which a liquid rises in a capillary tube is_____proportional to the radius of the tube and ________proportional to the surface tension of the liquid.
View SolutionThe force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
View SolutionThe force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
View SolutionThe potential energy of the liquid of surface tension T and density ρ that rises into the capillary tube is
View SolutionWhen a liquid is in contact with a solid the angle between the surface of the solid and the tangent drawn to the surface of the liquid at the point of contact , measured in the side of the liquid is
View Solution