A metallic rod of length l and cross-sectional area A is made of a material of Young's modulus Y. If the rod is elongated by an amount y,then the work done is proportional to
Y
1/Y
Y2
1/Y2
The correct Answer is:C
To solve the problem, we need to find the relationship between the work done on a metallic rod and the elongation it experiences when subjected to a tensile force. Let's break it down step by step.
Step 1: Understand the Definitions
- Young's Modulus (Y): It is defined as the ratio of stress to strain in a material. Mathematically, it is given by:
Y=StressStrain
- Stress: It is defined as the force (F) applied per unit area (A):
Stress=FA
- Strain: It is defined as the change in length (ΔL or y) divided by the original length (L):
Strain=yL
Step 2: Relate Stress and Strain
From the definition of Young's modulus, we can express stress in terms of Young's modulus and strain:
Stress=Y×Strain=Y×yL
Step 3: Calculate the Work Done
The work done (W) on the rod when it is elongated can be expressed using the formula:
W=12×Stress×Strain×Volume
The volume (V) of the rod is given by:
V=A×L
Substituting the expressions for stress and strain into the work done formula:
W=12×(Y×yL)×(yL)×(A×L)
Step 4: Simplify the Expression
Now, substituting the volume into the work done expression:
W=12×Y×yL×yL×(A×L)
This simplifies to:
W=12×Y×A×y2L
Step 5: Identify Proportionality
From the simplified expression, we can see that the work done (W) is proportional to the square of the elongation (y):
W∝y2
Conclusion
Thus, the work done is proportional to the square of the elongation of the rod.
Final Answer
The work done is proportional to y2.
---
- Young's Modulus (Y): It is defined as the ratio of stress to strain in a material. Mathematically, it is given by:
Y=StressStrain
- Stress: It is defined as the force (F) applied per unit area (A):
Stress=FA
- Strain: It is defined as the change in length (ΔL or y) divided by the original length (L):
Strain=yL
From the definition of Young's modulus, we can express stress in terms of Young's modulus and strain:
Stress=Y×Strain=Y×yL
The work done (W) on the rod when it is elongated can be expressed using the formula:
W=12×Stress×Strain×Volume
The volume (V) of the rod is given by:
V=A×L
Substituting the expressions for stress and strain into the work done formula:
W=12×(Y×yL)×(yL)×(A×L)
Now, substituting the volume into the work done expression:
W=12×Y×yL×yL×(A×L)
This simplifies to:
W=12×Y×A×y2L
From the simplified expression, we can see that the work done (W) is proportional to the square of the elongation (y):
W∝y2
Thus, the work done is proportional to the square of the elongation of the rod.
The work done is proportional to y2.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Chapter Exercise73videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Match the columns4videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Check point 12.215videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions469videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer17videos
ELECTROSTATICS
Similar Questions
A metal rod of length l, cross-sectional area A, Young's modulus Y and coefficient of linear expansion α is heated to t∘C. The work that can be performed by the rod when heated is
View SolutionA uniform cylindrical rod of length L and cross-sectional area by forces as shown in figure.

The elongation produced in the rod isView Solution
Knowledge Check
- Question 1 - Select One
A wire of length L and cross-sectional area A is made of a material of Young's modulus Y. IF the wire is stretched by an amount x, the workdone is
AYAx22LBYAx2L2CYAx2LDYAx2L
A metal rod of length 'L' and cross-sectional area 'A' is heated through 'T'∘C What is the force required to prevent the expansion of the rod lengthwise ?
View SolutionCalculate the compressional force required to prevent the metallic rod of length l cm and cross sectional area Acm2 when heated through t∘C from expanding lengthwise. Young's modulus of elasticity of the metal is E and mean coefficient of linear expansion is α per degree celsius.
View SolutionA uniform cylindrical rod of length L, cross-section area A and Young's modulus Y is acted upon by the force as shown in Fig. 7(CF).3. The elongation of the rod is
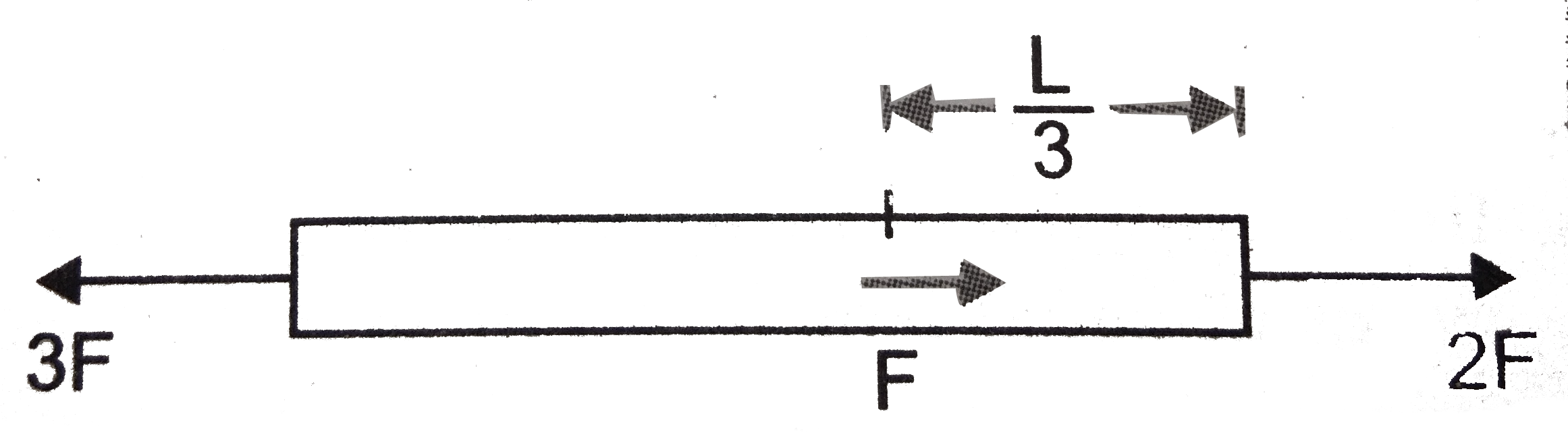 View Solution
View SolutionA uniform rod of length l, mass m, cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity ω. Find the total extension in the rod due to the tension produced in the rod.
View SolutionA smooth uniform, string of natural length l, cross-sectional area A and Young’s modulus Y is pulled along its length by a force F on a horizontal surface. Find the elastic potential energy stored in the string.
View SolutionFor most of the material , Young's modulus (Y) and rigidity modulus (G) are related as
View SolutionCalculate the compressional force required to prevent the metallic rod length lcm and cross-sectional area Acm2 when heated through t∘C, from expanding along length wise. The Young's modulus of elasticity of the metal is E and mean coefficient of linear expansion is α per degree Celsius
View Solution
