In a modified YDSE, sources S is kept in front of slit S1. Find the phase difference at point O that is equidistant from slits S1 and S2 and point P that is in front of slit S1 in the following situations.
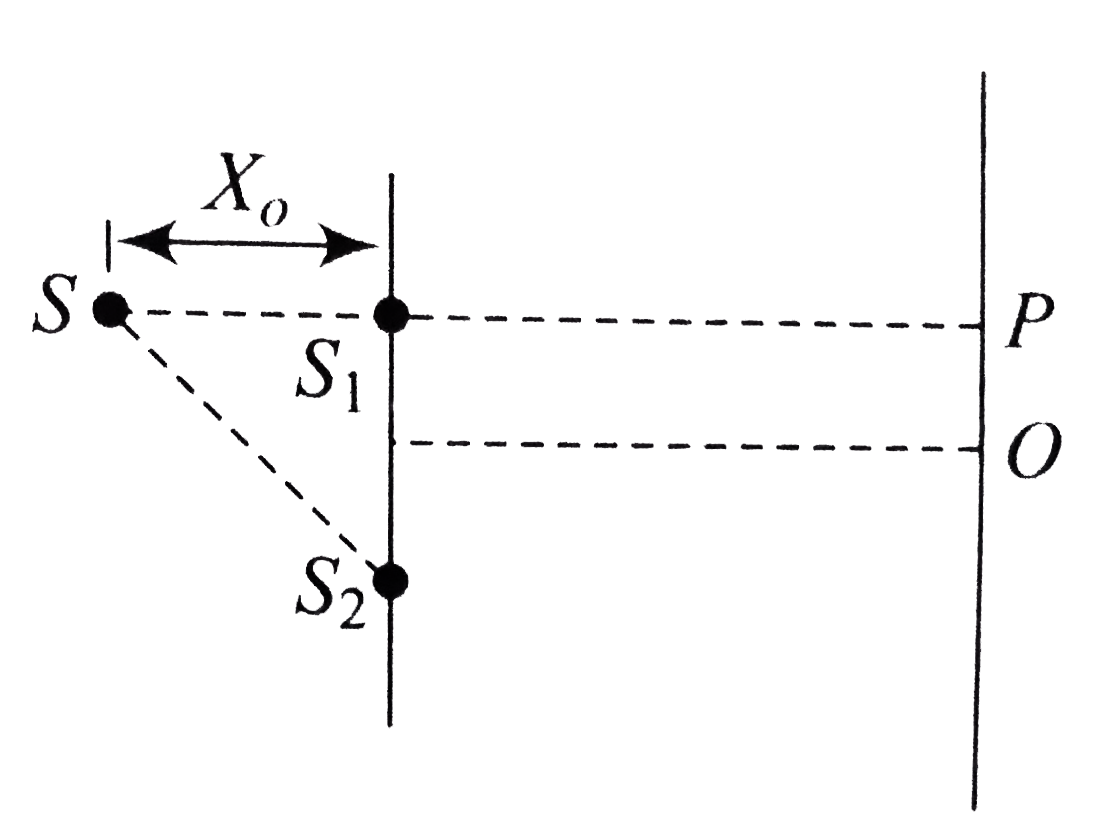
A liquid of refractive index μ is filled between the screen and slits.
2πλ.[√d2+x20+x0]+μd22D]
2πλ.[[√d2+x20−x0]+μd22D]
2πλ.[[√d2−x20+x0]+μd22D]
2πλ.[[√d2−x20−x0]+μd22D]
The correct Answer is:b
While calculating path difference, it must be remembered that is is equal to difference of optical path lengths from sources S to point on the screen.
∴Δxtotal=[Δx]before slits+[Δx]after slits
=(SS2−SS1)+(S2P−S1P) ltbgt a. When liquid is filled between the slits and screen, then
[S2P]liquid=[μS2P]air
[S1P]liquid=[μS1P]air
At point O: μS2O=μS1O
Noth path difference is introduced after slits. So,
Δxtotal=SS2−SS1=√d2+X20−x0
Thus, phase diffenence,
Δϕ=2πλ(√d2+X20−x0)
At point P: [Δx]before slits=√d2+x20−x0
[Δx]after slits=μS2P−μS1ap=μ(S2P−S1P)
=μydD=μd22D(asy=d2)
Thus phase difference,
Δϕ=2πλ[(√d2+x20−x0)+μd22D]
b. When liquid is filled between the source and slits:
At point O: (Δx)before slits=(SS2+SS1)liquid
(μSS2+μSS1)air
=μ(√d2+x20−x0)
(Δx)after slits=S2O+S1O=0
(Δx)total=μ(√d2+x20−x0)
Thus, phase differnce at P,
Δϕ=2πλ(μ√d2+x20−x0)
At point P: (Δx)before slits=(SS2+SS1)liquid=(μSS2+μSS1)air
(Δx)after slits=(S2P−S1P)air=ydD=d22D
(Δx)total=[(μ√d2+x20−x0)+d22D]
Thus, phase difference at P,
Δϕ=2πλ[μ√D2+x20−x0+d22D]
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Integer3videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Archives4videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning13videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type12videos
SOURCES OF MAGNETIC FIELD
Similar Questions
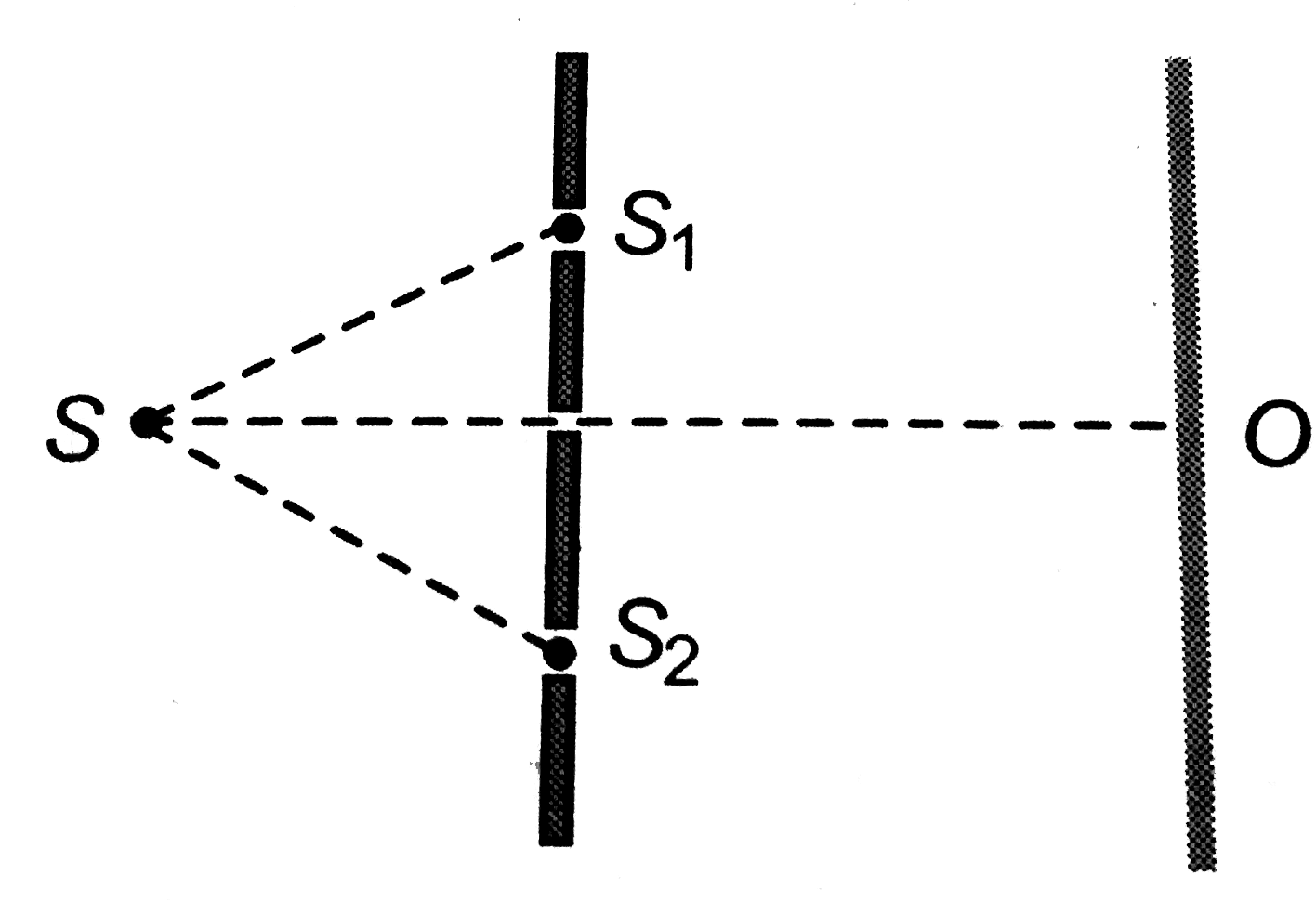
In the set up shown in figure, the two slits S1 and S2 are not equidistant from the slit S. The central fringe at O is then
 View Solution
View SolutionIn the YDSE apparatus shown in figure Δx is the path difference between S2PandS1P. Now a glass slab is introduced in front of S2, then match the following.


View SolutionMonochromatic light of wavelength λ passes through a very narrow slit S and then strikes a screen placed at a distance D = 1m in which there are two parallel slits S1 and S2 as shown. Slit S1 is directly in line with S while S2 is displaced a distance d to one side. The light is detected at point P on a second screen, equidistant from S1 and S2 When either slit S1 or S2 is open equal light intensities I are measured at point P. When both slits are open, the intensity is three times as large i.e. 3I. If the minimum possible wavelength is Nd2, then find the value of N(d<<D)
 View Solution
View SolutionIn figure S is a monochromatic source of light emitting light of wavelength of wavelength λ (in air). Light on slits S1 from S and then reaches in the slit S2 and S3 through a medium of refractive index μ1. Light from slit S2 and S3 reaches the screen through a medium of refractive index μ3. A thin transparent film of refractive index μ2 and thickness t is used placed in front of S2. Point P is symmetrical w.r.t. S2 and S3. Using the values d=1mm,D=1m,μ1=4/3,
μ2=3/2,μ3=9/5, and t=49×10−5m,
a. find distance of central maxima from P,
b. If the film in front of S2 is removed, then by what distance and in which direction will be central maxima shift ?
 .View Solution
.View SolutionIn the arrangement shown in figure, light of wavelength 6000Å is incident on slits S1 and S2 have been opened such that S3 is the position of first maximum above the central maximum and S4 is the closest position where intensity is same as that of the ligth used, below the central maximum Point O is equidistant from S1 and S2 and O' is equidistant from S3 and S4. Then intensity of inciden light is I0

Find the intensity at O' (on the screen).View SolutionIn the arrangement shown in figure, light of wavelength 6000Å is incident on slits S1 and S2 have been opened such that S3 is the position of first maximum above the central maximum and S4 is the closest position where intensity is same as that of the ligth used, below the central maximum Point O is equidistant from S1 and S2 and O' is equidistant from S3 and S4. Then intensity of inciden light is I0

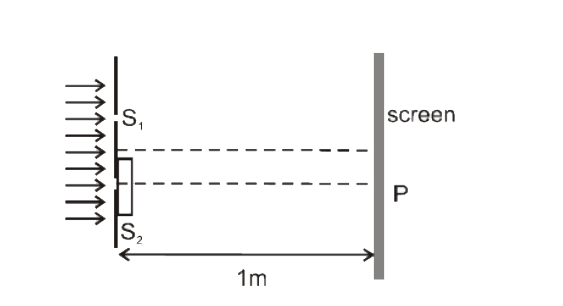
Find the intensity of the brightest fringe.View SolutionIn standard Young's double - slit experiment, visible light λ∈(350nm,750nm) is used in both the slits. Distance between the slits is 2 mm, and the distance of the screen from the slits is 1 m. A thin glass slab (μ=1.5) of thickness 6μm is placed in front of slit S2. Which among the following wavelength is missing at point P, which is directly in front of slit S2? (Neglect dispersion of light)
 View Solution
View SolutionAt two point P and Q on screen in Young's double slit experiment, waves from slits S1 and S2 have a path difference of 0 and λ4 respectively. The ratio of intensities at P and Q will be:
View SolutionIn YDSE arrangement as shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 Å (in air). S1and S2 are two slits seperated by d = 1 mm and D = 1m. Left of slits S1 and S2 medium of refractive index n1=2 is present and to the right of S1 and S2 medium of n2=32, is present. A thin slab of thickness 't' is placed in front of S1 . The refractive index of n3 of the slab varies with distance from it's starting face as shown in figure.

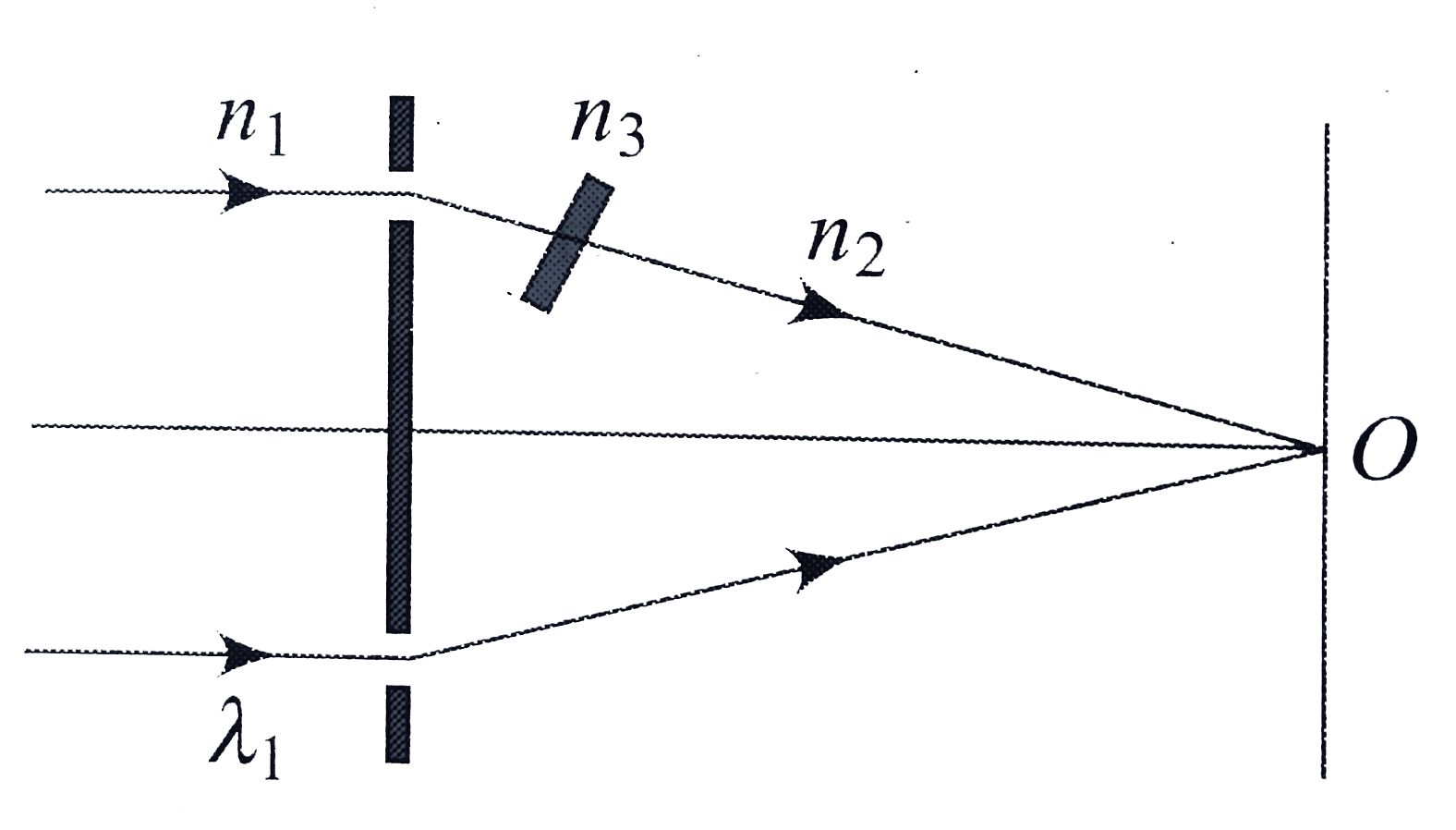
In order to get central maxima at the centre of screen, the thickness of slab required is :View SolutionIn YDSE shown in figure a parallel beam of light is incident on the slits from a medium of refractive index n1. The wavelength of light in this medium is λ1. A transparent slab of thickness t and refractive index n3 is put in front of one slit. The medium between the screen and the plane of the slits is n2. The phase difference between the light waves reaching point O (symmetrical, relative to the slits) is
 View Solution
View Solution
