Question

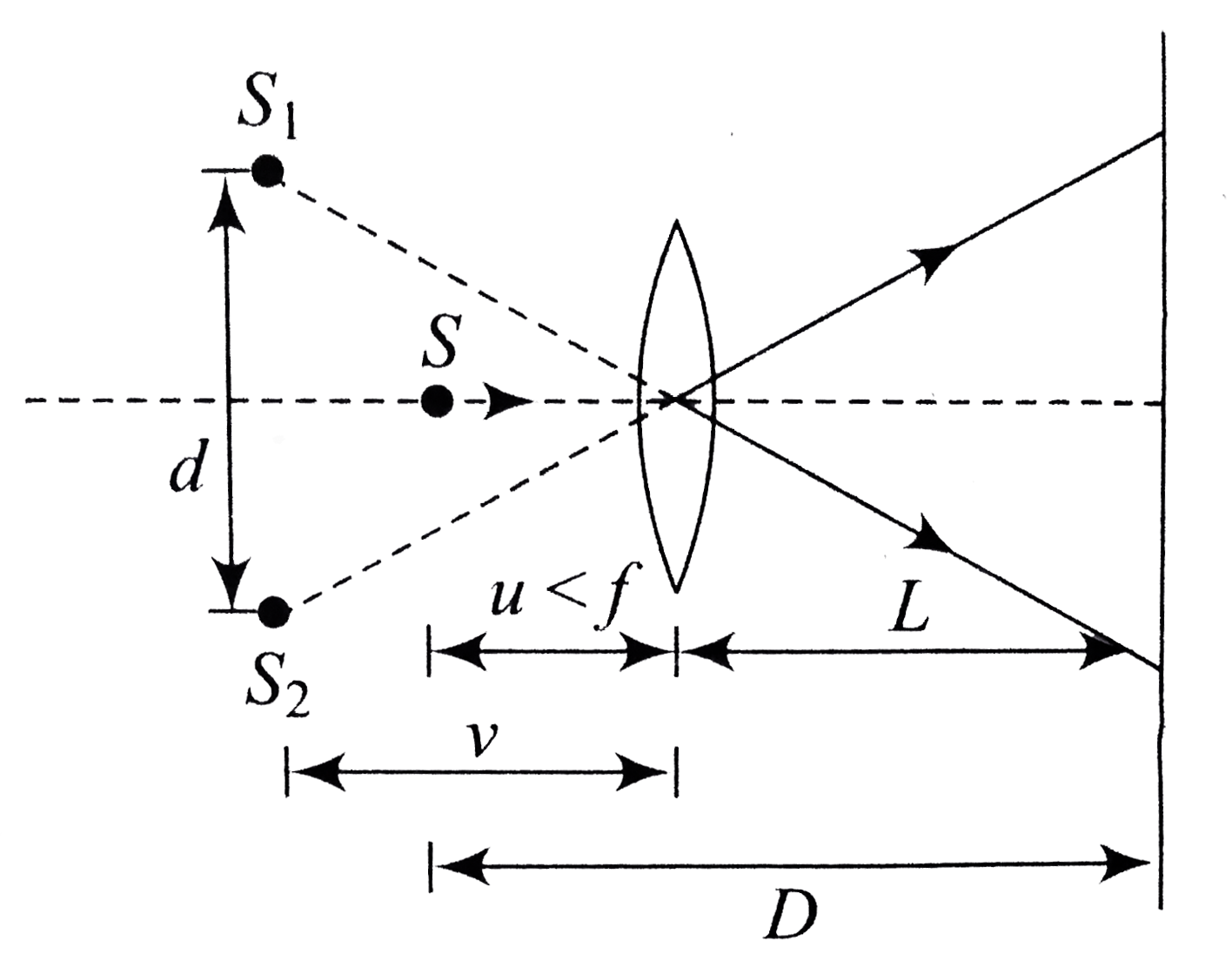
A lens of focal length f is cut along the diameter into two identical halevs. In this process, a layer of the lens t in thickness is lost, then the halves are put together to form a composite lens. In between the focal plane and the composite lens, a narrow slit is placed near the focal plane. The slit is emitting monochromatic $\lambda$. Behind the lens, a screen is located at a distance L front it.

The expression for the number of visible maxima which are obtained through above said arrangement will turn out to be

Options

A. `(L t^(2))/(lambda f^(2))`
B. `(2L t^(2))/(lambda f^(2))`
C. `(L t)/(2 lambda f^(2))`
D. `(L t^(2))/(2 lambda f^(2))`

Answer

d

Explanation

From lens equation, we have
`v = (u f)/(f - u)`
`d = 2 ((1)/(2)) [(v)/(u) - 1] = t [(u)/(f - u)]`
`D = L + v = L + (u f)/(f - u)`
Fringe width,
`beta = (lambda D)/(d) = [[lambda [ L + (u f)/(f - u)])/(t [(u)/(f - u)]]]`
`beta = (lambda)/(t) [f + (L(f - u))/(u)]`
When `u rarr f, beta = (lambda f)/(t)`
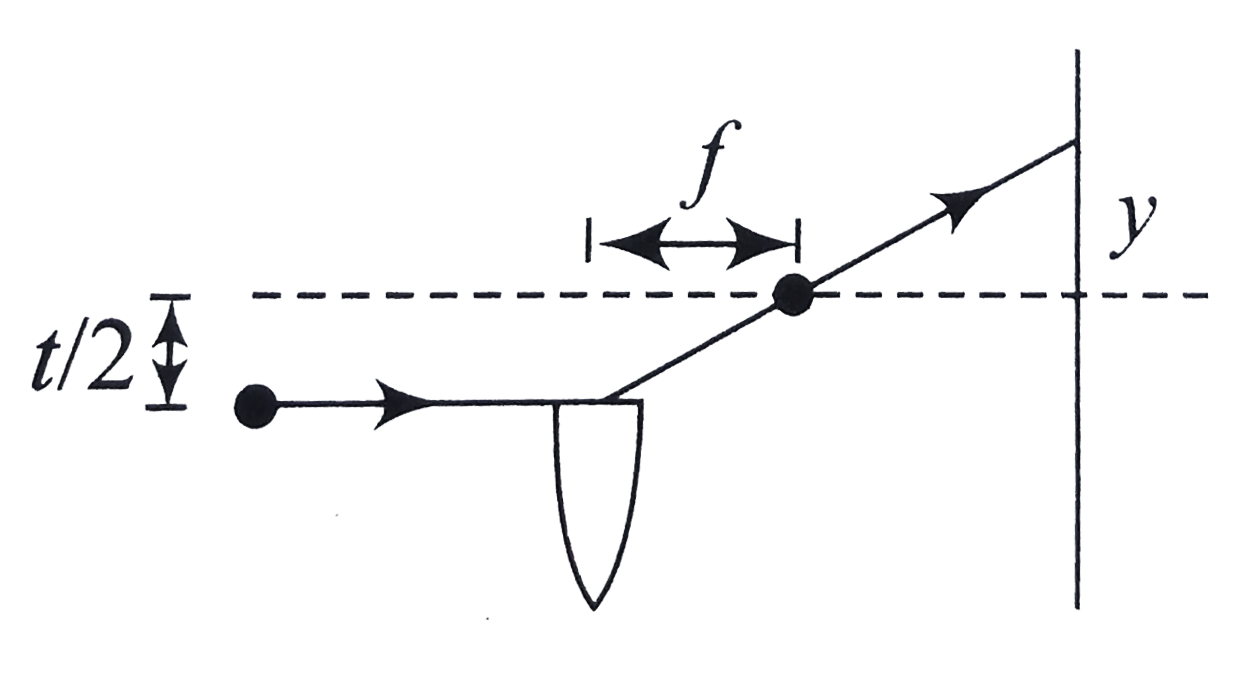
From the figure,
`(y)/(L - f) = (t // 2)/(f) implies y = (t // 2)/(f) (L - f)`
distance of the point up to which interference occurs,
`y_(0) = (t // 2)/(f) (L - f) + (t)/(2) = (tL)/(2f)`
Number of visible maxima `= (t L t)/(2 f xx lambda f) = (L t^(2))/(2 lambda f^(2))`
.